Взаимодействие скважин при нестационарных процессах

Метод суперпозиции фильтрационных потоков используется и в задачах неустановившихся процессов при упругом режиме.

Группа скважин. Так, если в пласте действует группа скважин, в числе которых имеются как эксплуатационные, так и нагнетательные скважины, понижение давления в какой-либо точке пласта Dр определяется сложением понижений давлений, создаваемых в этой точке отдельными источниками и стоками, изображающими скважины Dр_j. Следовательно,

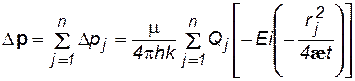, (7.29)

где n–число скважин;Q_j – объемный дебит стока (+) или источника(-) за номером j; r_j– расстояние данной точки пласта от скважины за номером j.

Так как аргумент интегрально-показательной функции мал (меньше 1), то зависимость (7.29) можно переписать в виде

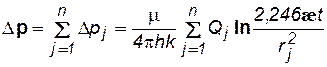. (7.30)

Данная зависимость используется для расчета параметров пласта путем обработки кривой восстановления давления в случае скважины, эксплуатирующейся в течение длительного времени и остановленной для исследования.

Периодически работающая скважина. В неограниченном пласте останавливается скважина, эксплуатирующаяся с постоянным дебитом Qв течении времениТ,сравнимого со временем проведения исследований. Понижение давления Dр^/ в момент времени Тможно найти по формуле (7.23). С момента остановки давление в ней и окружающей области пласта повышается, т.е. с данного момента в одном и том же месте пласта как бы действуют совместно и непрерывно эксплуатационная (сток) и нагнетательная (источник) скважины. При этом источник имеет тот же дебит Q. Обозначим повышение давления за счет работы источника через Dр^//. Таким образом, начиная с момента времени Т, на основании формулы (7.23) имеем:

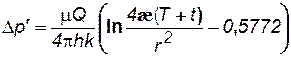, (7.31)

.

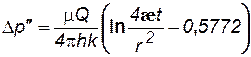Результирующее понижение давления Dр в любой точке пласта находится по методу суперпозиции

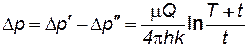. (7.32)

Обозначая через р_сдавление на забое скважины после её остановки, получаем

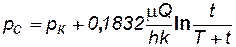. (7.33)

Зависимость (7.33) используется при гидродинамических исследованиях скважин, работающих не продолжительное время, методом построения кривой восстановления давления.