в трещиновато-пористом и трещиноватом пластах
Уравнение неразрывности фильтрационного потока в (чисто) трещиноватом пласте строится на основе тех же самых рассуждений, которые были приведены в предшествующих параграфах этой главы.
При построении уравнений неразрывности для трещиновато-пористого пласта следует учитывать характерные особенности такого пласта: во-первых, то, что трещиновато-пористый пласт моделируется системой двух сред с порами разных масштабов (среда 1, где роль поровых каналов играют трещины, а роль зёрен — пористые блоки; среда 2 — обычная пористая среда, образующая пористые блоки); во-вторых, между отмеченными выше средами при фильтрации возникает переток жидкости из пористых блоков в трещины в пределах выделенного элементарного объема трещиновато-пористого пласта. При этом предполагается, что в каждом элементарном объеме трещиновато-пористого пласта содержится большое число пористых блоков (т. е. размер блоков мал по сравнению с характерным размером элементарного объема пласта), так что в окрестности каждой точки трещиновато-пористой среды вводятся две скорости фильтрации, два давления, относящиеся к средам 1 и 2. На основании сказанного уравнения неразрывности выписываются для каждой из сред, составляющих трещиновато-пористый пласт; при этом переток жидкости из пористых блоков в трещины при фильтрации в каждой из сред учитывается членом q1;2.
 Следовательно, для жидкости, находящейся в трещинах (среда 1), будем иметь уравнение неразрывности такого вида:
Следовательно, для жидкости, находящейся в трещинах (среда 1), будем иметь уравнение неразрывности такого вида:
(VIII.19)
 Уравнение неразрывности для жидкости, находящейся в пористых блоках (среда 2), с учетом перетока из блоков в трещины внутри вы деленного элемента трещиновато-пористого пласта можно представить как:
Уравнение неразрывности для жидкости, находящейся в пористых блоках (среда 2), с учетом перетока из блоков в трещины внутри вы деленного элемента трещиновато-пористого пласта можно представить как:
(VIII.20)
В уравнениях (VIII.19) и (VIII.20) q1;2 — масса жидкости, по ступающей из пористых блоков в трещины за единицу времени на единицу объема; она имеет размерность: 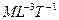 .
.
Полагая, что величина q1;2, характеризующая переток, пропорциональна разности фильтрационных потенциалов первой и второй сред, уравнения неразрывности для трещиновато-пористого пласта окончательно получаем в виде:
 (VIII.21)
(VIII.21)
где 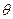 — коэффициент переноса, размерности
— коэффициент переноса, размерности 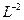 .
.
 Здесь
Здесь 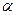 — безразмерный параметр трещиновато-пористой среды, характеризующий обмен жидкостью между системой пористых блоков и трещин.
— безразмерный параметр трещиновато-пористой среды, характеризующий обмен жидкостью между системой пористых блоков и трещин.
Выражение для q1;2 в этом случае следует из нашего: при упрощающих предположениях относительно вязкости и плотности.
Для (чисто) трещиноватого пласта естественно считать, что q1;2 = 0 и тогда на основании (VIII.19) имеем только одно уравнение неразрывности для жидкости в системе трещин (в пористых блоках не содержится жидкость):
 (VIII.22)
(VIII.22)
 При установившейся фильтрации жидкости в трещиновато-пористом пласте, когда во всем пласте существует только одно поле давления (р1 = р2 = р3) и величины плотности жидкости
При установившейся фильтрации жидкости в трещиновато-пористом пласте, когда во всем пласте существует только одно поле давления (р1 = р2 = р3) и величины плотности жидкости 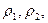 скорости фильтрации
скорости фильтрации 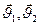 , а также
, а также 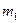 и
и 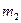 не зависят от времени, тогда получаем:
не зависят от времени, тогда получаем:
 (VIII.23)
(VIII.23)
Для чисто трещиноватого пласта имеем:
(VIII.24)
[1] Под «точкой» понимается введенный выше элементарный объём порового пространства.
[2] Напомним, что по физическому смыслу число Рейнольдса представляет собой отношение сил инерции к силам вязкого трения.
[3] Давлением насыщения называется давление газа, находящегося в термодинамическом равновесии с пластовой нефтью.
Дата добавления: 2020-03-17; просмотров: 875;











