Пласте с круговым контуром питания.

по формуле 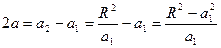(см. рис. 19) на контуре скважины:

(VII.25)

Подставляя в формулу (VII.7) (УIТ.7) сначала данные условия (VII.24), а затем данные (VII.25), вычитая почленно одно равенство из другого и решая полученное уравнение относительно М, найдем:

(VII.26)

Такой вид имеет формула массового дебита эксплуатационной скважины, заложенной эксцентрично в пласт с круговым контуром области питания. Для одиночной нагнетательной скважины дебит вычисляется по формуле (VII.26), но перед правой частью ставится знак минус.

Из формулы (VII.26) легко получается формула (IV.25) для плоско-радиального потока, т. е. для случая скважины, расположенной концентрично относительно кругового контура питания пласта: если скважина находится в центре пласта, то достаточно в формуле (VII.26) положить 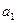= 0; тогда получим формулу типа формулы Дюпюи.

Влияние на дебит скважины расстояния от нее до контура пласта можно определить по формулам (VII.23 и (VII.26): чем дальше от внешнего контура пласта находится скважина, тем меньший дебит она имеет.

Дебит скважины в случае, в котором действительный контур пласта есть произвольный контур, будет промежуточным между дебитами, рассчитанными по формулам (VII.23) и (VII.26), т. е. между дебитами при прямолинейном и круговом контурах.

Не рискуя допустить неприемлемую в технических расчетах ошибку при вычислении дебита скважины, можно применить любую из двух формул (VII.23) или (VII.26).

Таким образом, чем ближе расположена скважина к контуру питания, тем меньшее значение имеет форма внешнего контура, т. е. при вычислении дебита скважины форма внешнего открытого контура пласта не имеет сколько-нибудь существенного значения.