От нагнетательной скважины к эксплуатационной

Пусть сток О₁ и источник О₂ равнодебитны, т. е. имеют одинаковые по модулю массовые дебиты М; О₁О₂ = 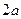. Исследуем поток от источника к стону.

Проведем ось Ох через точки О₁ и О₂ так, чтобы точка О₁ находилась от начала координат О на расстоянии 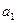, а точка О₂ на расстоянии 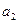(рис. 19).

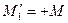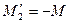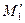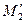По формуле (VII.2) определим потенциальную функцию сложного потока. По принятому здесь обозначению для дебита стока запишем: ; для дебита источника . После подстановки значений и в формулу (VII.2) получим:

(VII.7)

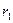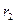где и расстояния любой точки пласта до стока и источника соответственно.

Уравнение изобар (VII.4) в данном случае будет следующим:

(VII.8)

Каким кривым соответствует уравнение (VII.8)? Чтобы ответить на этот вопрос, выразим прежде всего 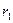и 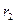через координаты точки М (х, у) в соответствии с рис. 19.

(VII.9)

Подставляя значения 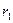и 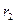из (VII.9) в уравнение (VII.8), получим:

(VII.10)

Уравнение (VII.10) характеризует эквипотенциальные линии изобары.

Запишем уравнение (VII.10) в таком виде:

Рис. 19. Схема стока О₁ и источника О₂.

(VII.11)

Где зависимость постоянной С₁ от радиуса окружности В удобно представлять в таком виде

или (VII.11а)

Из уравнения (VII.11) видно, что эквипотенциальные линии — окружности, центры которых расположены на оси Ох (в уравнении отсутствует член, содержащий первую степень у).

Итак эквипотенциальные линии (изобары) при совместном действии одной эксплуатационной и одной нагнетательной равнодебитных скважин в неограниченном пласте представляют собой окружности, центры которых расположены на прямой, проходящей через центры скважин. Среди окружностей есть одна, имеющая бесконечно большой радиус - прямая, которая делит расстояние между скважинами и всю плоскость течения пополам. Половина всех окружностей конечного радиуса R расположена по одну сторону от этой прямой, остальные окружности — по другую (рис. 20). Семейство линий тока в данном случае есть семейство окружностей, ортогональных изобарам. Все линии тока проходят через стон и источник. Центры всех окружностей линии тока расположены на прямой, делящей расстояние между стоном и источником пополам (см. рис. 20).

Таково фильтрационное поле, поддерживаемое стоном и источником одинаковой мощности.

Выведем формулу массового дебита М эксплуатационной и нагнетательной скважин при совместном их действии.

для вывода формулы М следует принять граничные условия. Граничными контурами в данном случае являются контуры обеих скважин.

Предположим, что на контуре эксплуатационной скважины О₁ радиусом 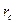потенциальная функция 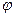принимает значение 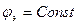, определяемое в зависимости от давления с точностью до произвольной постоянной, а на контуре нагнетательной скважины О₂ того же радиуса .

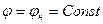Рис. 20. Фильтрационное поле источника и стока.

Воспользуемся формулой (VII.11). На контуре эксплуатационной скважины имеем 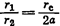(см. рис. 19); на контуре нагнетательной скважины

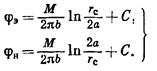(VII.12)

Вычитая почленно из второго равенства (VII.12) первое и решая полученное уравнение относительно М, найдем, что

(VII.13)

Определим массовую скорость фильтрацию в любой точке пласта М (см. рис. 19). Если бы в пласте действовал только один стон О₁ с дебитом, модуль которого равнялся М, мы получили бы, согласно

формуле (IV.18), следующее выражение модуля вектора массовой скорости :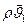

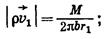(VII.14)

если бы действовал только один источник О₂ с дебитом М, можно было бы записать:

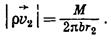(VII.15)

Суммируя по принципу суперпозиции векторы массовых скоросте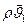й и 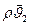вычислим модуль массовой скорости в данной точке пласта 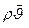(см. рис. 19).

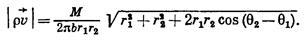(VII.16)

Но величина корня квадратного правой части (VII.16) есть расстояние между стоком и источником О₁О₂ = 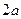; следовательно, фор мулу (VII.16) перепишем так:

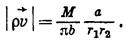(VII.17)

Для поддержания в нефтяной залежи пластового давления, обеспечивающего высокую отдачу нефти пластом, на промыслах широко используется способ нагнетания воды в пласт через нагнетательные скважины.

Вычислим для однородной несжимаемой жидкости время движения частицы по кратчайшему пути между нагнетательной и эксплуатационной скважинами т. е. по оси Ох.

для несжимаемой жидкости равенство (VII.17) можно записать так:

или для частицы D, движущейся по оси Ох от Оy к О₁ (см. рис. 19).

(VII.18)

где х-абсцисса частицы D, движущейся по оси Ох.

Если начало координат поместим в стоке О₁, то применительно к частице D будем иметь:

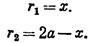
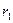Подставляя эти значения и 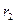в уравнение (VII.18), разделяя в нем переменные и интегрируя, получаем:

(VII.19)

Время Т прохождения частицей расстояния О₁О₂ = 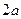определится из (VII.19), если принять х = 0, х₀ = 2а:

(VII.20)

Общий объем внедренной в пласт воды за время Т равен 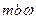где 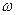— обводненная площадь. Этот объем воды можно подсчитать также по формуле (VII.20):

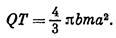
Приравнивая оба выражения объема, найдем обводненную площадь за время Т:

(VII.21)

По формулам (VII.19) и (VII.20) нетрудно установить, что за время Т, за которое одна частица воды пройдет расстояние 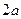от нагнета тельной скважины до эксплуатационной, а другая частица, вошедшая в пласт извне одновременно с первой, но движущаяся в

положительном направлении оси Ох, пройдет расстояние вдвое меньшее, т. е. равное 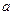. Таким образом, площадь, обводнившаяся к моменту времени Т, вытянута в сторону эксплуатационной скважины.

Итак, мы исследовали поток от нагнетательной скважины к эксплуатационной. Исследование потока в случае двух скважин — одной эксплуатационной и одной нагнетательной в неограниченном пласте служит основой изучения нерадиального плоского потока в случаях одной и многих скважин в пласте, границы которого с областью питания находятся на конечном расстоянии от скважины. Приведенный же способ определения дебита будет применяться и в последующих задачах, но без подробных вычислений.