О методе исследования плоского потока
В настоящей главе рассматривается плоский нерадиальный поток, поддерживаемый в пластле одной или несколькими эксплуатационными и нагнетательными скважинами.
Если нет специальных оговорок, везде предполагается, что пласт - горизонтальный, имеющий всюду одинаковую мощность. Сверху он перекрыт непроницаемой горизонтальной кровлей, а подстилается горизонтальной непроницаемой подошвой. Движение жидкости или газа в пласте подчиняется закону фильтрации Дарси и является установившимся.
Во всех параграфах настоящей главы рассматривается плоское движение жидкости (газа) в пористой среде. Это значит, что изучается движение, происходящее в плоскостях, параллельных между собой и что картина движения во всех плоскостях представляется одинаковой. Будем разбирать движение в одной из этих плоскостей — в основной плоскости течения.
К решению задач настоящей главы мы будем применять принцип суперпозиции (наложения) потоков. Основанный на этом принципе метод суперпозиции заключается в следующем.
При совместном действии в пласте нескольких стоков (источников) потенциальная функция (или давление), определяемая каждым стоком (источником), вычисляется по формуле для единственного стока. Потенциальная функция, обусловленная всеми стоками и источниками, вычисляется путем алгебраического сложения этих независимых друг от друга значений потенциальной функции.
Пусть в неограниченном по протяженности пласте действует одна эксплуатационная скважина (сток) с положительным массовым дебитом М. (Если бы скважина была нагнетательной, она являлась бы источником и её дебит был бы отрицательным). Поток, поддерживаемый стоком с дебитом М,- плоско-радиальный. Потенциальная функция 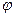 определяется формулой (IV.20):
определяется формулой (IV.20):
 (VII.1)
(VII.1)
где 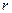 — расстояние между некоторой точкой пласта и центром скважины; С — постоянная.
— расстояние между некоторой точкой пласта и центром скважины; С — постоянная.
Допустим, что дебит 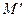 эта скважина имеет в случае, если она не единственная в пласте, а действует совместно с другой или с не сколькими скважинами того же пласта (эксплуатационными и нагнетательными). Пользуясь методом суперпозиции, найдем выражение потенциальной функции сложного потока
эта скважина имеет в случае, если она не единственная в пласте, а действует совместно с другой или с не сколькими скважинами того же пласта (эксплуатационными и нагнетательными). Пользуясь методом суперпозиции, найдем выражение потенциальной функции сложного потока 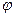 так:
так:
 (VII.2)
(VII.2)
где 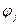 — выражение функции
— выражение функции 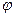 на контуре скважины за номером j;
на контуре скважины за номером j; 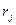 — расстояние между данной точкой пласта и скважиной за номе ром j;
— расстояние между данной точкой пласта и скважиной за номе ром j; 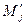 — массовый дебит этой скважины, положительный, если скважина эксплуатационная (сток), и отрицательный, если скважина нагнетательная (источник); n — общее число скважин; С — постоянная.
— массовый дебит этой скважины, положительный, если скважина эксплуатационная (сток), и отрицательный, если скважина нагнетательная (источник); n — общее число скважин; С — постоянная.
 Если жидкость несжимаемая, формулу (VII.2) можно записать, вводя вместо
Если жидкость несжимаемая, формулу (VII.2) можно записать, вводя вместо 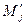 объёмный дебит
объёмный дебит 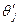 :
:
(VII.3)
 Для определения эквипотенциальных линий — изобар заметим, что во всех точках этих кривых значение
Для определения эквипотенциальных линий — изобар заметим, что во всех точках этих кривых значение 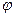 должно оставаться неизменным; следовательно, уравнение изобар получается, например, из (VII.2) путем приравнивания его правой части некоторой постоянной, и представляется в следующем виде:
должно оставаться неизменным; следовательно, уравнение изобар получается, например, из (VII.2) путем приравнивания его правой части некоторой постоянной, и представляется в следующем виде:
(VII.4)
где П — знак произведения; С1 – постоянная.
 Таково уравнение изобар в многополярной системе координат. Если дебит всех скважин как по величине, так и по знаку одинаковый, уравнение изобар записывается проще:
Таково уравнение изобар в многополярной системе координат. Если дебит всех скважин как по величине, так и по знаку одинаковый, уравнение изобар записывается проще:
(VII.5)
Линии тока образуют семейство кривых, ортогональных изобарам.
Чтобы вычислить дебиты 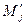 , воспользуемся граничными условиями: контуры всех скважин и контур питания пласта - изобары, радиусы скважин одинаковы; радиус скважины
, воспользуемся граничными условиями: контуры всех скважин и контур питания пласта - изобары, радиусы скважин одинаковы; радиус скважины 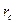 значительно меньше расстояния между скважинами и расстояния между скважинами и контуром питания пласта. для вычисления дебитов надо составить всего n + 1 уравнений, потому что столько будет неизвестных: n дебитов М и постоянная С1. Пусть значение
значительно меньше расстояния между скважинами и расстояния между скважинами и контуром питания пласта. для вычисления дебитов надо составить всего n + 1 уравнений, потому что столько будет неизвестных: n дебитов М и постоянная С1. Пусть значение 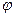 на контуре скважины за номером
на контуре скважины за номером 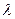 будет
будет 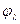 значение
значение 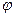 на контуре питания пласта
на контуре питания пласта 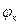 .
.
Подставив в уравнение (VII.2) порознь значения 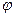 на каждой скважине и соответствующие этой скважине значения
на каждой скважине и соответствующие этой скважине значения 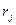 , получим n уравнений. Подставив значения
, получим n уравнений. Подставив значения 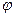 и
и 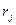 на контуре питания, получим еще одно уравнение. Окончательно будем иметь систему (n+ 1) — уравнение с n + 1 неизвестными:
на контуре питания, получим еще одно уравнение. Окончательно будем иметь систему (n+ 1) — уравнение с n + 1 неизвестными:
 (VII.6)
(VII.6)
i
 где
где 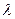 принимает значения 1, 2, ..., n, а
принимает значения 1, 2, ..., n, а 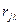 т — расстояния между скважинами за номерами j и
т — расстояния между скважинами за номерами j и 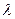 ; (VII.6a)
; (VII.6a)
где 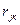 - расстояние между скважиной за номером j и контуром питания.
- расстояние между скважиной за номером j и контуром питания.
Для вычисления массовых дебитов остается решить систему уравнений (VII.6) относительно 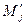 .
.
Итак, последовательность вывода формулы дебита следующая.
1. По методу суперпозиции составляется потенциальная функция потока 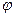 .
.
2. Устанавливаются граничные условия задачи.
З. В выражение потенциальной функции 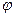 подставляются порознь значения переменных
подставляются порознь значения переменных 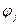 и
и 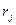 на граничных контурах пласта и скважин; составляется таким образом система уравнений с неизвестными массовыми дебитами
на граничных контурах пласта и скважин; составляется таким образом система уравнений с неизвестными массовыми дебитами 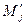 и постоянной С.
и постоянной С.
4. Полученная система уравнений решается относительно дебитов 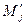 .
.
Дата добавления: 2020-03-17; просмотров: 689;











