Имеющем непроницаемую подошву

В главах IV и V движение жидкости в пласте рассматривалось при условии, что движущаяся жидкая масса заполняет поры или трещины выделенной области пласта на всем протяжении этой области по всей мощности пласта. Например, для прямолинейно-параллельного и плоско-радиального потоков предполагалось, что движение жидкости происходит во всех точках любого вертикального отрезка прямой, отсчитанного от непроницаемой подошвы пласта до его непроницаемой кровли. При этом напорная пьезометрическая поверхность располагалась выше кровли пласта. В настоящей главе рассматривается движение жидкости, поверхность которой остаётся ниже кровли пласта и совпадает с пьезометрической поверхностью.

Поверхность жидкости в рассматриваемых здесь случаях назовем свободной поверхностью жидкости, давление над поверхностью постоянное. При неподвижном состоянии жидкости свободная её поверхность горизонтальна; в процессе движения она искривляется, понижаясь в направлении потока.

В отличие от движения жидкости, пьезометрический уровень которой выше непроницаемой кровли пласта, движение жидкости со свободной поверхностью называют безнапорным движением.

Когда добывают нефть, безнапорное движение жидкости может происходить, например, в условиях определенной разновидности гравитационного режима пласта; вследствие истощения пластовой энергии уровень жидкости находится ниже кровли пласта.

Преобладающая форма пластовой энергии при разработке нефтяного месторождения с гравитационным режимом проявляется в действии силы тяжести жидкости.

Безнапорное движение жидкости в пласте встречается также при шахтной и карьерной разработке нефтяных месторождений.

Теория безнапорного движения жидкости в пористой среде особенно широко применяется при решении задач гидрогеологии, относящимся, например, к фильтрации воды через земляные плотины, к фильтрации грунтовой воды к колодцам и др.

Затруднительно найти точное решение некоторых задач безнапорного движения жидкости в пласте. Мы ограничимся изложением той приближенной теории безнапорного установившегося движения жидкости, которая известна под названием гидравлической теории Дюпюи — Форхгеймера.

Основным методом указанной приближенной теории безнапорной фильтрации служит метод осреднения потока по высоте. Представим продуктивный пласт, имеющий непроницаемую горизонтальную подошву. Пусть при отборе жидкости из пласта или при поглощении её пластом уровень жидкости устанавливается ниже кровли пласта. Если потоком жидкости со свободной поверхностью охвачена большая площадь, свободная поверхность потока бывает слабо искривлена. В этом случае задачи об осесимметричном безнапорном течении (к скважине или от скважины) и о безнапорном течении к прямолинейной галерее (или от галереи) могут быть сведены к задачам об одномерном потоке.

Рассмотрим один из этих двух видов безнапорного течения в любой из вертикальных плоскостей, в которой движутся все находящиеся в ней жидкие частицы.

Рис. 17 Схема пласта, в котором движется жидкость со свободной поверхностью

На рис. 17 изображено сечение ABCD вертикальной плоскостью координат rOz.

Наша координатная плоскость выбрана так, что она пересекает непроницаемую подошву пласта по оси Oz, кровлю — по линии DС, свободную поверхность жидкости — по кривой ЕFG.

Если пренебречь скоростным напором (вследствие малости скорости фильтрации), можно записать напор h следующим образом:

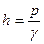, (VI.1)

где 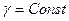— вес единицы объёма жидкости.

Напор h выражается в функции r и z — координат точек кривой ЕFG.

Следовательно, давление р выражается в функции тех же переменных:

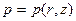. (VI.2)

Считая, что кривая ЕFG имеет малый наклон, будем пренебрегать вертикальными составляющими векторов скорости фильтрации. Тогда получим в плоскости rOz поток с параллельными горизонтальными скоростями.

Если принять, что во всех точках пласта, расположенных на одной вертикали, скорости не только параллельны, но и равны по величине, мы должны заключить, что и давления в точках одной вертикали будут одинаковыми.

Но из формулы (VI.2) следует, что давление выражается в функции двух переменных: r и z. Допущение о независимости давления р от координаты z — для точек одной вертикали равносильно тому, что в формуле (VI.2) мало изменяющаяся переменная z заменяется некоторой постоянной z_ср средней высотой потока. Таким образом давление р можно считать зависящим только от координаты r, а значит рассматриваемое безнапорное течение можно считать одномерным. В данном потоке напор h совпадает с высотой свободной поверхности жидкости.

Приняв указанные допущения, мы можем использовать дифференциальное уравнение одномерного потока (IV.18). Поскольку жидкость несжимаема и параметры k и 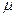постоянны, потенциальная функция 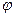выражается формулой: ,

где 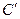- постоянная.

Подставим значение 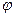, в уравнение (IV.18) и заметим, что величина А в этом уравнении для безнапорного потока имеет следующие значения:

А = 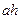- в случае притока в направлении к прямолинейной галерее, или в противоположную сторону;

А = 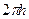- в случае осесимметричного потока к скважине или в противоположную сторону.

Учитывая, кроме того, что при сделанных нами допущениях имеет место равенство (VI.1), напишем дифференциальное уравнение без напорного потока в следующем виде:

(VI.3)

где 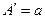— ширина потока прямолинейной галереи и 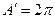— ширина истока для скважины; j = 0 — для галереи и j = 1 для скважины.

Интегрируя уравнение (VI.3) при условии, что j = 0, получим: (VI.4)

При j = 1 будем иметь (VI.5)

Произвольные постоянные C в формулах (VI.4) и (VI.5) определяются обычным порядком по граничным условиям задачи.

Поскольку дифференциальное уравнение безнапорного потока (VI.3) и формулы (VI.4), (VI.5) основаны на допущениях, связанных с методом осреднения потока по высоте, необходимо выяснить, в какой мере эти формулы отвечают реальным условиям.

Точные аналитические исследования в теории безнапорного потока и данные специальных экспериментов, проводившихся на песчаных и электрических моделях, показывают значительное несоответствие между действительной свободной поверхностью жидкости и поверхностью, определяемой по уравнениям (VI.3) - (VI.5). Использование формул (VI.4) (VI.5) при определении свободного зеркала жидкости возможно тем с большей точностью, чем выше уровень жидкости в стоке, чем большую протяженность имеет поток по сравнению с его мощностью и чем дальше от стока берутся уровни жидкости.

Установлено, однако, что при сходящемся или расходящемся осесимметричном потоке формула (VI.5) с достаточной точностью воспроизводит фактическое распределение высот по пласту. Для безнапорного потока в случае галереи по формуле (VI.4) получаем лишь грубое приближение к действительности. Несоответствие между действительными и расчетными уровнями жидкости в безнапорном движении объясняется влиянием капиллярного слоя, перекрывающего основную массу жидкости в пласте.

Но если имеется несоответствие между фактическими дан о свободной поверхности жидкости и результатами подсчетов высот уровней по формулам (VI.4) и (VI.5), то с помощью последних можно получить вполне приемлемые для практических целей формулы дебита.