Со свободной поверхностью
Чтобы получить формулы дебита, надо использовать граничные условия задачи.
Пусть на стенке, ограничивающей пласт с одной стороны, определяемой координатой 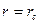 (см. рис. 17), высота уровня жидкости
(см. рис. 17), высота уровня жидкости 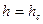 ; на противоположной стороне пласта, т. е. при
; на противоположной стороне пласта, т. е. при 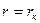 . Подставив в формулы (VI.4) и (VI.5) сначала величины
. Подставив в формулы (VI.4) и (VI.5) сначала величины 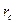 и
и 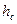 , а затем
, а затем 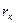 и
и 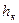 получим для каждой из формул по два уравнения, содержащих неизвестную С. Исключая С из каждой пары уравнений, найдем соответствующее значение
получим для каждой из формул по два уравнения, содержащих неизвестную С. Исключая С из каждой пары уравнений, найдем соответствующее значение 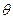 .
.
Для прямолинейной галереи из формулы (VI.4) следует
 (VI.6)
(VI.6)
где 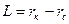 .
.
 Из формулы (VI.5) имеем дебит для осесимметричного безнапорного потока по закону Дарси:
Из формулы (VI.5) имеем дебит для осесимметричного безнапорного потока по закону Дарси:
(VI.7)
Формулы (VI.6) и (VI.7) называются формулами Дюпюи для безнапорного потока.
Обратимся к индикаторпым диаграммам. Введем величину понижения уровня свободной поверхности жидкости под статическим уровнем, высоту которого будем считать равной 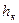 Обозначим понижение уровня, как и в главе IV через S. Имеем:
Обозначим понижение уровня, как и в главе IV через S. Имеем:
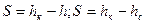 (см. рис. 17).
(см. рис. 17).
Для построения индикаторной диаграммы следует знать зависимость между 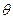 и
и 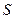 . Найдем ее с помощью закона Дарси. Она выводится из соответствующей формулы Дюпюи (VI.6) или (VI.7). Если обозначим совокупность постоянных множителей и делителей че рез Е, можем представить выражение дебита
. Найдем ее с помощью закона Дарси. Она выводится из соответствующей формулы Дюпюи (VI.6) или (VI.7). Если обозначим совокупность постоянных множителей и делителей че рез Е, можем представить выражение дебита 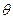 так:
так:
 (VI.8)
(VI.8)
 |  |
где - для осесимметричного потока; - для потока
 при действии галереи. Разность
при действии галереи. Разность  — в формуле (VI.8) можно видоизменить, введя понижение уровня
— в формуле (VI.8) можно видоизменить, введя понижение уровня 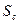 :
:

Подставляя найденное значение в равенство (VI.8), запишем:
(VI.9)
Индикаторная диаграмма, построенная по формуле (VI.9), имеет вид параболы с осью, параллельной оси дебитов (см. рис. 18).
Безнапорные подземные воды водоносного горизонта, залегающего на первом от поверхности водоупорном ложе, называют грунтовыми. При движении грунтовая вода обычно проникает в водоносный горизонт из вышележащих горизонтов или с поверхности земли. Это явление носит название инфильтрации. Инфильтрация происходит и в нефтеносных пластах, если они перекрываются или подстилаются проницаемыми, хотя и слабо, для жидкости пластами.
Дифференциальное уравнение безнапорного потока (VI.3) выведено нами без учета инфильтрации. Полученные на основе этого уравнения формулы дебита (VI.6) и(VI.7) можно, следовательно, применять к расчетам потоков, в которых инфильтрация или отдача жидкости в направлении перекрывающих или подстилающих пластов не играет существенной роли.

Рис. 18. Индикаторная кривая для безнапорного потока.
Глава VII
Дата добавления: 2020-03-17; просмотров: 712;











