Связь между символами плоскостей и направлений (граней и ребер).

Зная символы 2-х плоскостей можно найти символы ребра (направления), по которому они пересекаются и наоборот. Символы плоскости (hkl) и направления [mnp] связаны между собой: h m+k n+l p = 0. Найдем символы ребра [mnp] по которому пересекаются две грани (h₁k₁l₁) и (h₂k₂l₂). Для этого необходимо решить систему уравнений:

h₁ m + k₁n + l₁ p = 0

h₂ m + k₂ n + l₂ h = 0 (2.3)

Решением системы уравнений являются детерминанты:

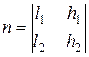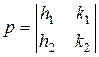, , (2.4)

а отношение det-ов дает символ грани:

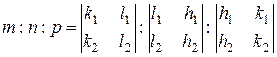(2.5)

Аналогично можно найти символы грани по символам двух, лежащих на ней ребер:

(2.6)

Обратная решетка.

Обратная решетка представляет собой удобную абстракцию, позволяющую математически просто и точно описывать условия, в которых протекает то или иное явление в твердом кристаллическом теле. Каждой кристаллической структуре соответствуют две решетки: кристаллическая решетка и обратная решетка. Они связаны между собой соотношениями:

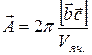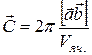; ; . (2.7)

- векторы обратной решетки; - векторы прямой решетки. Векторы кристаллической решетки имеют размерность длины, а размерность векторов обратной решетки [длина]^-1.

Так как , то скалярное произведение:

, (2.8)

. (2.9)

При построении обратной решетки векторы перепендикулярны соответственно , , и, обратно, векторы перпендикулярны парам векторов , , . Векторы прямой решетки связаны с векторами обратной решетки аналогичными формулами:

; ; ; (2.10)

где - объем элементарной ячейки обратной решетки: _.

Свойства обратной решетки:

1. обратная и прямая решетки взаимно сопряжены;

2. решетка обратная обратной, есть исходная прямая решетка;

3. каждый узел [[mnp]]* обратной решетки соответствует семейству параллельных плоскостей (hkl) прямой решетки;

4. обратная решетка Бравэ сама является решеткой Бравэ.

Векторы трансляции связывают в прямой кристаллической решетке пары точек, которые имеют одинаковые атомные окружения. В обратном пространстве также вводится понятие трансляций, которые описываются векторами обратной решетки, образующих следующее семейство:

, (2.11)

где h, k и l – целые числа.

Если прямая решетка строго периодична, то обратная решетка, т.е. множество точек, удовлетворяющих условию (2.11), также периодична и бесконечна. Однако для решения тех задач, где удобно пользоваться представлением об обратной решетки, достаточно бывает ограничиться конечными объемом обратного пространства.

Элементарную ячейку Вигнера-Зейтца для обратной решетки называют первой зоной Бриллюэна. Первая зона Бриллюэна является зоной с наименьшим объемом. Она полностью ограничена плоскостями, которые делят пополам перпендикулярные к ним векторы обратной решетки, проведенные из начала координат.