ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей (l=1,47Å). Определить расстояние между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда лучи падают под углом j =31⁰30¢.

РЕШЕНИЕ.

Из уравнения Вульфа-Брэгга найдем межплоскостное расстояние:

.

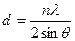Угол q является дополнительным углом к углу j: q = 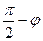= 58⁰30`. Подставим числовые значения:

d = 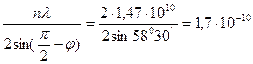м=1,7 Å=0,17 нм.

ОТВЕТ: 0,17 нм.

Пример 2: Кристаллы меди имеют гранецентрированную кубическую решетку. При комнатной температуре ребро элементарного куба равно 3,608Å. Монокристалл меди вырезан параллельно одной из граней элементарного куба. Пусть на поверхность кристалла падает монохроматический пучок рентгеновских лучей с длиной волны 1,658 Å. Показать, что плоскости, параллельные поверхности, будут отражать рентгеновские лучи, если угол между пучком и поверхностью кристалла приближенно равен 27⁰ или 67⁰.

РЕШЕНИЕ.

Как известно, отражение от кристалла возникает в том случае, если выполняется условие Вульфа-Брэгга: 2d sin q = nl.

Откуда sin q = nl/2d. При n = 2 : sin q = l/d = 1,658/3,608 » 0,4595; q » 27⁰.

При n = 4: sin q₂ = 2l/d = 2 ×1,658/3,608 » 0,9190; q » 67⁰.

ОТВЕТ: При n = 2 q»27⁰, при n = 4 q » 67⁰.

Пример 3: Какое максимальное число линий может появиться на рентгенограмме от простой кубической решетки с постоянной а=2,86×10^-8см, если исследование ведется на кобальтовом излучении с длиной волны 1,789×10^-8см.

РЕШЕНИЕ.

По формуле Вульфа-Брэгга для кубической решетки:

.

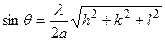Так как максимальное значение sinq=1, то ;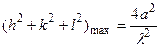

(h²+k²+l²)_max=10,2. Следовательно, на рентгенограмме появятся линии от плоскостей, у которых сумма квадратов индексов Миллера не превышает 10, а именно:

(hkl) (100) (110) (111) (200) (210) (211) (220) (300) (310)

h²+k²+l² 1 2 3 4 5 6 8 9 10.

ОТВЕТ: 9 линий.