РАЗДЕЛ 3. Дифракция в кристаллах

Изучение атомной структуры вещества основано на явлениях дифракции в нем рентгеновских лучей, электронов или нейтронов. Теория дифракции, изучающая связь картины рассеяния с пространственным расположением атомов, для всех трех излучений одинакова. Для получения дифракционной картины существенно, чтобы длина волны используемого излучения была сравнима со средним межатомным расстоянием. Расстояния между атомами заключены в пределах 1-4 Å. В случае волн видимого света, имеющих длину тысячи ангстрем, дифракция не наблюдается. Рентгеновские лучи, нейтроны и электроны, имеющие длину волны ~1Å, дают интерференционные эффекты при рассеянии скоплениями атомов. Дифракционные методы исследования структуры являются расчетными. С помощью дифракции волн в кристалле получают данные о размере элементарной ячейки, положениях ядер и распределении электронов внутри ячейки. Для расчетов необходимо знать положение интерференционных максимумов, возникающих при рассеянии излучения на узлах кристаллической решетки. Дифракцию на кристаллах можно интерпретировать, как “отражение” лучей (при использовании рентгеновского излучения - рентгеновских лучей) плоскостями кристаллической решетки (рис.5).

Рис. 5.

“Отражение” происходит лишь тогда, когда волны, рассеянные параллельными плоскостями, оказываются в фазе и усиливают друг друга, то есть, когда разность хода при рассеянии от соседних плоскостей равна целому числу n длин волн l:

nl=2d_hklsinq. (3.1)

Это формула Вульфа-Брэгга, связывающая направления распространения рассеянных пучков (углы q) с межплоскостными расстояниями d_hkl в решетке; n- порядок отражения. Формула Вульфа-Брэгга показывает, что дифракционные пучки для данного d_hkl могут быть получены в монохроматическом излучении, то есть при постоянном l, за счет изменения ориентации кристалла (углов q), а при неподвижном кристалле - в полихроматическом излучении отражение возникает при соответствующей длине волны l.

Если объект, на который падает начальная волна, состоит из n-рассеивающих центров с рассеивающей способностью f_j, расположенных в точках r_j, то амплитуда результирующей волны будет равна:

. (3.2)

Вектор 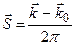, , 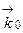- волновой вектор падающей волны, 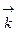- рассеянной волны, F(S) - амплитуда рассеяния данного объекта. При падении рентгеновских лучей (электромагнитная волна) на объект физическими “точками”, рассеивающими эти волны, являются электроны. Каждый из них становится источником вторичной рассеянной волны той же частоты и той же длины волны, что и начальная. Если принять амплитуду рассеяния одним электроном равной единице, то амплитуда рассеяния будет равна:

. (3.3)

Функция электронной плотности. Вместо дискретного набора n-точек, находящихся в положениях , рассматривают непрерывно распределенную рассеивающую способность объекта. Так как рентгеновские лучи рассеиваются электронами, то “рассеивающей матрицей” для них является средняя во времени электронная плотность объекта r( 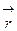). Эта функция равна среднему числу электронов n_e( ) в элементе объема DV_r около точки , деленному на элемент объема:

. (3.4)

Атомная амплитуда (атомный фактор). Интенсивность рентгеновских отражений пропорциональна рассеивающей способности атома в кристаллической решетке. Падающая на атом плоская монохроматическая волна возбуждает в каждом его элементе объема dV элементарную вторичную волну. Амплитуда этой рассеянной волны, пропорциональна рассеивающей способности данного элемента объема, которая в свою очередь пропорциональна r( )dV_r. Число, показывающее, во сколько раз амплитуда суммарной волны, рассеиваемой атомом больше амплитуды волны, рассеиваемой электроном, при тех же условиях (т.е. под тем же углом и для той же длины волны), есть f-атомный фактор рассеяния атома некоторого элемента с радиальной функцией распределения U(r):

(3.5)

При малых sin q/l отношение синуса к аргументу близко к единице и f = , z - число электронов в атоме (атомный номер элемента).

Температурный фактор. Атомы в кристалле находятся в состоянии теплового движения. Функция электронной плотности, которая определяет рассеяние, есть средняя во времени электронная плотность. Длительность дифракционного эксперимента намного превышает периоды тепловых колебаний атомов. Чтобы учесть тепловое движение нужно знать функции w(r), дающие среднее во времени распределение центров атомов около их положения равновесия

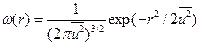, где 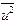- среднее квадратичное смещение атома из положения равновесия. Температурный фактор

f_т(S) = exp (-2p 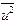S²). (3.6)

Условие Лауэ. Вывод уравнений Лауэ основывается на следующих соображениях: если твердое тело находится в кристаллическом состоянии, то обязательно имеется направление, вдоль которого все идентичные по свойствам узлы располагаются параллельными рядами и в каждом таком ряду они связаны трансляцией а. Если на такой ряд направить под произвольным углом a₀ параллельный пучок монохроматического излучения с длиной волны l, то отражение будет происходить только в тех направлениях, для которых все взаимно складывающиеся отражения от узлов, связанных между собой трансляцией а, находятся в одной фазе (рис.6).

Это возможно, если разность хода между волнами, рассеянными от двух соседних узлов, равна целому числу длин волн:

D=a(cos a - cos a₀) = h l, (3.7)

где a - угол между направлением отражения и направлением ряда; h - индекс интерференции (целое число).

Рис.6.

В трехмерно-периодической решетке с трансляциями a, b, c уравнения Лауэ записываются в виде:

a(cos a - cos a₀) = h l,

b(cos b - cos b₀) = k l, (3.8)

c(cos g - cos g₀) = l l.

Три уравнения Лауэ, определяющие направления интерференционных лучей в пространстве можно в общем случае заменить одним интерференционным уравнением, позволяющим интерпретировать условие интерференции геометрически с помощью обратной решетки:

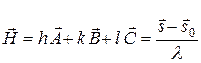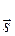; где и 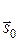- направляющие косинусы падающего и отраженного лучей соответственно. Это уравнение полностью определяет положение интерференционных лучей и содержит как уравнение Лауэ, так и уравнение Вульфа-Брэгга. Используя его можно путем геометрического построения обратной решетки и сферы отражения (сферы Эвальда) определять направление интерференционных лучей.

Структурный фактор. Если элементарные ячейки двух каких-либо различных веществ подобны по форме и тождественны по размерам, то геометрическое расположение рефлексов на рентгенограммах всегда совершенно одинаково, независимо от того содержит ли ячейка всего один, два или весьма большое число атомов. Если элементарные ячейки подобны по форме, но имеют разные размеры, то геометрическое расположение на соответствующих рентгенограммах отличается лишь масштабом. Различие геометрически тождественных рефлексов наблюдается в интенсивностях. Интенсивности части рефлексов равны нулю (т.е. просто отсутствуют). Отличие в интенсивностях геометрически тождественных рефлексов обусловлено различием рассеивающей способности атомов, входящих в элементарную ячейку, ядра которых имеют разные заряды z. Учет этого отличия производится с помощью введения в формулу для интенсивности отраженных от кристалла лучей - структурного фактора F²_hkl, равного квадрату структурной амплитуды F_hkl. Структурная амплитуда - величина, характеризующая рассеяние элементарной ячейкой, выраженное в электронных единицах, т.е., отнесенное к рассеянию электрона, в тех же условиях (те же q и l). Каждому hkl соответствует своя структурная амплитуда F_hkl. Выражение для структурной амплитуды имеет вид

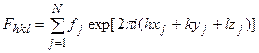, (3.9)

где х_j , y_j , z_j - координаты j-го базисного атома в ячейке, f_j - атомный рассеивающий фактор j-го атома, N- число базисных атомов. Амплитуда волны, рассеянной одной элементарной ячейкой кристалла, равна произведению амплитуды волны, рассеянной электроном и структурной амплитуды. На структурном факторе (амплитуде) сильно сказываются кристаллографические особенности кристаллической структуры: ее элементы симметрии, тип решетки, пространственная группа симметрии.