Интегральный закон погасаний.

1. ОЦК-решетка. Базис ОЦК-решетки состоит из двух одинаковых атомов с координатами {{000}} {{ 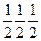}}, т.е. для одного из атомов х₁=y₁=z₁=0 , а для другого х₂=y₂=z_{2= .} Тогда структурный фактор имеет вид: F_hkl=f{1+exp[ip(h+k+l)]}, где f-рассеивающая способность отдельного атома. При четной сумме индексов (h+k+l) структурная амплитуда отлична от нуля. При нечетной сумме (h+k+l) дополнительные слагаемые (h+k+l)/2 изменяют фазу на 180⁰, изменяя знак экспоненты. В этом случае амплитуда равна нулю. Все отражения hkl с нечетной суммой индексов для структуры с ОЦК -решеткой гаснут. Физический смысл того, что в дифференциальной картине для ОЦК - решетки отсутствуют отражения (100) состоит в следующем. Для присутствия отражения необходимо чтобы, лучи, отраженные от первой и третьей плоскости (они ограничивают элементарный куб) имели разность фаз 2p. Дополнительная промежуточная плоскость в ОЦК - решетке, расположена посредине между плоскостью 1 и 3. Отраженный от нее луч сдвинут по фазе относительно луча, отраженного первой плоскостью на p, поэтому отражения от нее гасит отражение от первой плоскости. Если плоскости в ОЦК - решетке состоят из разных атомов, то такого гашения не будет.

2. ГЦК - решетка. Базис ГЦК - решетки состоит из четырех одинаковых атомов с координатами {{000}}; {{0 1/2 1/2}}; {{1/2 0 1/2}}; {{1/2 1/2 0}}. Тогда структурный фактор принимает вид

F_hkl = f{1+exp[ip(k+l)] + exp[ip(h+l)]+ exp[ip(h+k)]}. (3.10)

Если все (h+k), (h+l), (k+l) - четные, то все слагаемые равны по модулю и знаку. Это имеет место, когда hkl - либо все одновременно четные, либо все одновременно нечетные. Если индексы смешанные (т.е. одни из них четные, а другие нечетные и наоборот), то в этих случаях одна пара членов уничтожает другую и структурная амплитуда равна нулю. Таким образом, в ГЦК - решетках гаснут все отражения hkl со смешанными индексами.