РАЗДЕЛ 2. Внутренняя структура твердых тел. Обратная решетка

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Пусть энергия частицы в поле другой частицы зависит от расстояния между центрами этих частиц следующим образом:

U(r) = - 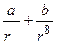, (1.10)

где a и b - постоянные. Показать, что:

1. Эти две частицы образуют стабильное соединение при r = r₀ = (8b/a)^1/7;

2. В случае образования стабильной конфигурации энергия притяжения в 8 раз больше энергии отталкивания;

3. Полная потенциальная энергия двух частиц при стабильной конфигурации

U_ст.= - = - ; (1.11)

4. Если удалять частицы друг относительно друга, то молекула разорвется, как только будет достигнуто расстояние R,

где R = 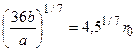. (1.12)

Решение

1. В состоянии равновесия

; (1.13) или 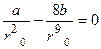, (1.14)

откуда r₀ = 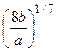. (1.15)

2. Энергия притяжения

U_пр.= - ; (1.16)

энергия отталкивания

U_от = 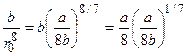. (1.17)

Сравнивая U_пр и U_от, получим |U_пр| = 8 U_{от .} (1.18)

3. Полная энергия

U = U_пр + U_от = - a . (1.19)

4. Молекула будет разорвана при максимальной силе F_max. Так как

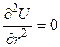F = - , то из уравнения находим межатомное расстояние, соответствующее максимальной силе:

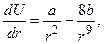(1.20)

. (1.21)

Из выражения (1.21) r_max = 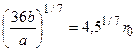. (1.22)

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО

РЕШЕНИЯ

1.1. Известно, что в кристалле, в котором связи обусловлены силами Ван-дер-Ваальса, равновесное межатомное расстояние r₀ = 1,50 Å, а энергия на 10% меньше, чем в случае, когда учитываются только силы притяжения. Чему равна характерная длина r, входящая в выражение: U = - . ОТВЕТ: r » 0,25 Å.

1.2. Энергия взаимодействия между двумя атомами в молекуле зависит от расстояния следующим образом:

U(r) = - .

Межатомное расстояние в положении равновесия r₀ = 3Å, энергия диссоциации (энергия расщепления нейтральной молекулы на противоположно заряженные ионы) молекулы U_д = - 4 эВ. Вычислить значения коэффициентов a и b, если n = 2, m = 10. Найти силы, стремящиеся вернуть атомы в положение равновесия при изменении межатомного расстояния r₀ на 10 %.

ОТВЕТ: a = 7,16×10^-38 Дж×м²; b = 9,44×10^-115 Дж×м¹⁰; F = 2,13×10^-9 Н.

1.3. Вычислить значение энергии кристаллической решетки NaCl, если постоянная n, характеризующая потенциал сил отталкивания, равна 9,4 , а постоянная Маделунга 1,75. Постоянная решетки NaCl равна 2,81 Å.

ОТВЕТ: U = 8,6× 10^-5 Дж/моль.

1.4. Экспериментальное значение энергии сцепления KCl на молекулу равно 6,62 эВ. Вычислить n, считая r₀ = 3.1 Å и a = 1,75.

ОТВЕТ: n » 5,37.

1.5. Показать, что модуль всестороннего сжатия кубической кристаллической решетки

В = ,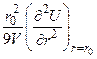

где r₀ - расстояние между атомами в состоянии равновесия; V- объем кристалла.

ОТВЕТ: В = .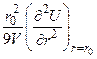

1.6. Вычислить энергию отталкивания для КСl, если энергия диссоциации равна (- 4,40) эВ. Принять r₀ = 2,79 Å, энергию ионизации атома калия равной 4,34 эВ, энергию сродства атома хлора к электрону – (-3,82 эВ).

ОТВЕТ: U_от = 0,24 эВ.

1.7. Найти сжимаемость кристалла NaCl при 0К, считая, что показатель экспоненты, определяющий величину сил отталкивания, равен m = 9,4. Постоянная Маделунга для NaCl равна 1,75.

ОТВЕТ: æ = 3,3 ×10^-11 м²/Н.

1.8. Рассмотреть к каким возможным последствиям для постоянной решетки, сжимаемости и энергии решетки, приведет удвоение заряда хлористого натрия, если считать, что потенциал отталкивания останется постоянным.

ОТВЕТ: Энергия решетки при увеличении заряда вдвое возрастет более чем в 4 раза, а сжимаемость уменьшится более чем в 4 раза.

1.9. Определить значение постоянной Маделунга для одномерной решетки, состоящей из последовательно чередующихся положительных и отрицательных ионов.

ОТВЕТ: a = 2ln2 = 1,386.

1.10. Используя метод, предложенный Эвьеном, вычислить значение постоянной Маделунга для кристалла типа NaCl.

ОТВЕТ: a = 1,75.

1.11. Получить выражение для модуля всесороннего сжатия кристалла с молярным объемом V₀ и общей энергией взаимодействия между атомами U_0, считая, что энергия взаимодействия между атомами определяется выражением U(r) = - .

ОТВЕТ: çВç= çU₀ç× .

РАЗДЕЛ 2. Внутренняя структура твердых тел. Обратная решетка

При сближении частиц на относительно больших расстояниях появляются силы притяжения, быстро увеличивающиеся с уменьшением расстояния r между частицами, а на малых расстояниях возникают силы отталкивания, которые с уменьшением расстояния r увеличиваются значительно быстрее, чем силы притяжения. На расстоянии r = r₀ силы отталкивания уравновешивают силы притяжения, и результирующая энергия взаимодействия достигает минимального значения (рис.1).

Рис. 1.

Поэтому состояние частиц, сближенных на расстояние r₀, является состоянием устойчивого равновесия, вследствие чего частицы выстраиваются в строгом порядке на расстоянии r₀ друг относительно друга, образуя тело с правильной внутренней структурой - кристалл. Такая структура будет сохраняться до тех пор, пока энергия связи остается выше по абсолютному значению энергии теплового движения частиц. Частицы кристалла не могут свободно покидать свои положения равновесия, так как при удалении от этих положений энергия частиц увеличивается и появляются силы, стремящиеся вернуть их в положение равновесия. При этом частицы совершают беспорядочное колебание около положений равновесия. Кристаллы -это вещества, в которых составляющие их частицы (атомы, молекулы) расположены строго периодически, образуя геометрически закономерную кристаллическую структуру. Каждое кристаллическое вещество отличается от других кристаллических веществ по его атомной структуре. Вследствие закономерности и симметрии структуры кристаллы однородны и анизотропны. Кристалл называется однородным,если для любой точки, взятой внутри него, найдется точка, совершенно идентичная по свойствам первой и отстоящая от нее на некотором конечном расстоянии. Анизотропность -это зависимость свойств кристалла от направлений в кристалле. Идентичные точки (узлы), связанные с произвольно выбранной точкой тремя некомпланарными векторами переноса (трансляциями), образуют трехмерную периодическую решетку, охватывающую все пространство кристалла. Положение любой частицы в такой решетке определяется вектором 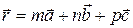. Векторы называются наименьшими векторами трансляции, а численные их величины – периодами трансляции.

Решетка, построенная путем параллельного переноса (трансляции) какого-либо узла по трем направлениям, называется трансляционной решеткой или решеткой Бравэ. Наименьший параллелепипед, построенный на векторах , называют элементарной ячейкойкристалла. Все элементарные ячейки, составляющие решетку, имеют одинаковые форму и объем. Элементарные ячейки, содержащие частицы только в вершинах, называют простыми, или примитивными.На каждую такую ячейку приходится одна частица.

Элементарные ячейки, содержащие частицы не только в вершинах, но и в других точках, называют сложными. Базисом ячейки называют совокупность координат узлов, приходящихся на элементарную ячейку. Координационным числомрешетки называется число ближайших соседей, окружающих данный атом.

Наиболее распространенные сложные ячейки: объемноцентрированные (ОЦ), базоцентрированные (БЦ) и гранецентрированные (ГЦ) (рис. 2).

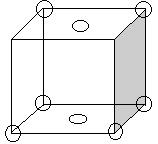Решетка, при построении которой можно транслировать не один узел, а несколько узлов (базис) называется решеткой с базисом.

ОЦ БЦ ГЦ

Рис. 2.

Всегда можно выбрать примитивную ячейку, которая обладала бы полной симметрией решетки Бравэ. Такой является ячейка Вигнера-Зейтца. При построении ячейки Вигнера-Зейтца произвольно выбранный узел обратной решетки соединяют прямыми линиями с ближайшими эквивалентными узлами; затем проводят плоскости, перпендикулярные этим прямым и проходящие через их середину. В результате получают замкнутую область пространства с центром в выбранном узле, все точки которой лежат ближе к нему, чем к любому другому узлу решетки (рис.3).

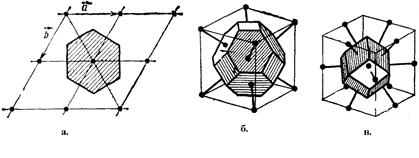
Рис. 3. Ячейка Вигнера-Зейтца: а - двухмерный случай; б - для объемно-центрированной кубической решетки; в – для гранецентрированной кубической решетки.

Некоторым твердым телам свойственна не одна, а две и более кристаллические структуры, устойчивые при различных температурах и давлениях. Такие структуры называют полиморфными формами или модификациями вещества, а переход от одной модификации к другой - полиморфными превращениями.Полиморфные модификации принято обозначать греческими буквами: модификацию, устойчивую при нормальной и более низкой температуре, обозначают буквой - a; модификации, устойчивые при более высоких температурах, обозначают соответственно буквами - b, g, d и т.д.

Узлы, направления и плоскости в решетке обозначают так называемыми индексами Миллера.

Положение любого узла решетки относительно выбранного начала координат определяется заданием трех его координат x, y, z:

x = ma; y = nb; z =pc, (2.1)

где a, b, c- параметры решетки; m, n, p - целые числа. Числа m, n, p - называют индексами узла и записывают так: [[mnp]]. Для отрицательного индекса знак минус ставится над индексом.

Для описания направления в кристалле выбирается прямая, проходящая через начало координат и любой узел, находящийся в этом ряду (направлении, ребре). Индексы узла являются одновременно и индексами направления. Индексы направления обозначают так: [mnp]. Индексы направления представляют собой три наименьших целых числа, характеризующих положение ближайшего узла, лежащего в данном направлении. Если ряд (или ребро) не проходит через начало координат, то необходимо мысленно перенести его в начало координат параллельно самому себе (так как все параллельные направления в кристалле равнозначны).

Положение плоскости определяется заданием трех отрезков А, В, С, которые она отсекает на осях решетки.

Чтобы найти индексы Миллера любой кристаллографической плоскостинадо:

1. выбрать начало координат, но не в данной плоскости;

2. выразить отрезки А, В, С, отсекаемые плоскостью на осях координат, через осевые отрезки а, b, с;

3. найти величины обратные этим отрезкам: 1/А, 1/В, 1/С;

4. полученные дроби привести к общему знаменателю D.

5. полученные три числа h=D/A; k=D/B; l=D/C заключить в круглые скобки (hkl). (hkl) - являются индексами плоскости (грани).

Чтобы построить плоскость (hkl) нужно нанести на осях координат отрезки a/h, b/k, c/l , через полученные таким образом точки будет проходить плоскость семейства {hkl}, ближайшая к началу координат.

Индицирование кристаллов гексагональной и тригональной сингоний. В этом случае для обозначения плоскостей пользуются четырехосной системой координат: три оси (а₁, а₂, а₃), расположенные под углом 120⁰ друг по отношению к другу, лежат в основании шестигранной призмы (в плоскости базиса), четвертая ось (с) перпендикулярна плоскости базиса (рис.3). Каждая плоскость обозначается четырьмя индексами: h, k, i, l. Дополнительный индекс i ставится на 3-м месте и вычисляется через индексы h и k : i = - (h+k).

Рис. 4.

Определение символов плоскостей (граней) по методу косинусов.Положение любой плоскости кристалла (hkl) вполне определяется углами, которые составляют нормаль к этой плоскости с осями координат. Для кубического кристалла

h:k:l = cosa: cosb: cosg. (2.2)