Поэтому ключ хорошо проводит как аналоговые, так и импульсные сигналы и в прямом и в обратном направлениях. В связи с этим мультиплексоры можно использовать как демультиплексоры.

Микросхема К564КП1 (рисунок 11.6) – двойной четырехканальный мультиплексор. Функциональная схема состоит из общей схемы управления, представляющий собой преобразователь логических уровней входных управляющих сигналов, дешифратора 2:4 и восьми двунаправленных ключей, разделенных на две синхронно работающих группы по четыре ключа в каждой.

Управление осуществляется по двум адресным входам А и В и разрешающему входу 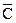. При наличии на входе 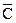низкого уровня любой из четырех возможных комбинаций на входах А и В соответствует один открытый канал в каждом мультиплексоре одновременно. При подаче на вход 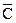высокого уровня все ключи размыкаются, каналы – закрыты. Вход 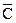имеет абсолютный приоритет перед любым другим входом управления. В мультиплексорах использован модифицированный ключ (рисунок 11.7). Кроме основных транзисторов VT1 и VT2 в ней введен дополнительный ключ VT3, VT4 и управляющий транзистор VT5. Благодаря использованию в мультиплексоре модифицированного ключа сопротивление открытого канала мало и имеет слабую зависимость от изменения входного сигнала в диапазон коммутируемых напряжений U_П1…U_П2. Питание осуществляется от двух источников питания. Разность напряжения U_П2 – U_П1 должна быть не более 15 В. Это позволяет коммутировать сигналы с амплитудой до 15 В, лежащие в диапазоне U_П2 ¸ U_П1.

Например, питание может быть «0 ¸ +15 В», « – 7, 5 В ¸ +7, 5 В», « – 3 В ¸ +3 В», « ‑10 В ¸ +5 В». В диапазоне этих питающих напряжений можно располагать коммутируемый сигнал. Максимальный допустимый ток через открытый ключ не более 10 мА.

Рисунок 11.6 –Условное графическое обозначение:

а − ИС К564КП1; б − функциональная схема

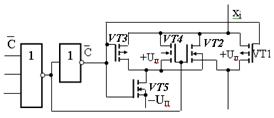
Рисунок 11.7 – Принципиальная схема канала

Микросхема К564КП2– восьмиканальный мульти-плексор, предназначенный для переключения цифровых и аналоговых сигналов (рисунок 11.8).Функциональная схема состоит из преобразователя логических уровней, дешифраторов и восьми двунаправленных аналоговых ключей. Управление вентильными ключами производится выходными сигналами дешифратора, которые вырабатываются под воздействием трехразрядного двоичного кода А В С. Нормальная работа микросхемы обеспечивается при нулевом напряжении на разрешающем входе V, при лог. 1 выходные ключи разомкнуты. Неискаженная передача аналоговых сигналов обеспечивается выбором питающих напряжений и схемой их подключения. Для питания микросхемы имеются три вывода. Ножка 8 служит общим выводом, 16 – «+Е_П» и 7 – «– Е_П».

Максимальное напряжение, прикладываемое к двум выводам микросхемы, не должно превышать 15 В.

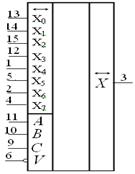
Рисунок 11.8 – Условное обозначение К564КП2

11.5 Синтез комбинационных схем на мультиплексорах

Мультиплексор является универсальным логическим элементом. Эта особенность основана на использовании общих свойств переключательных функций равняться логической единице или нулю при любом числе аргументов:

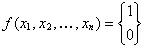
Если на адресные входы мультиплексора подать входные переменные, на информационные входы – значения лог. 0 или лог. 1 в соответствии с переключательной таблицей, то на входе получим значение нулей и единиц в соответствии с программой. Например, необходимо реализовать на мультиплексорах функцию «равнозначности»:

Функция имеет уровень лог. 1 на наборах x₂ x₁ = 00 и x₂ x₁ = 11 и уровень лог. 0 на наборах x₂ x₁ = 01 и x₂ x₁ = 10 (таблица 11.1). Для реализации данной функции необходимо подать на адресные входы мультиплексора сигнала x₂x₁, на входы D0 и D3 – потенциал высокого уровня U¹, на входы D1 и D2 - потенциалы низкого уровня U⁰ и на разрешающий вход V – уровень логического нуля U⁰, как показано на рисунке 11.9. При переборе входных адресов на выходе будет формироваться заданная переключательная функция.

Рисунок 11.9 – Реализация функции «равнозначность»

При синтезе схем с тремя аргументами f (x₂ x₁ x₀) в качестве адресных сигналов можно взять любые две переменные, например, x₂ x₁, тогда выходная функция будет определяться третьей переменной x₀, принимающей значения лог. 0 или лог.1 (const 0 или const 1). При этом возможны всего лишь четыре значения входной функции: 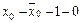. В качестве примера рассмотрим реализацию переключательной функции трех переменных, представленной в таблице 11.2. Поскольку переменные x₂ x₁ определяют номер подключаемого входа (D0 D1 D2 D3), то сигнал, действующий на данном входе, определяется информацией, расположенной в двух соседних клетках. Как показано в таблице 11.3, на входе D0 действует сигнал 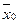, на входе D1 – const 1, на входе D2 – const 0 и на входе D3 – x₀. Схемная реализация этой переключательной функции приведена на рисунке 11.10. В общем случае при реализации функции n переменных n-1 аргумент является адресной частью и определяет требуемое количество входов мультиплексора – 2^{n – 1}. Следовательно, функция четырех переменных может быть реализована на восьмивходовых мультиплексорах, пяти переменных – на шеснадцативходовых мультиплексорах и т.д.

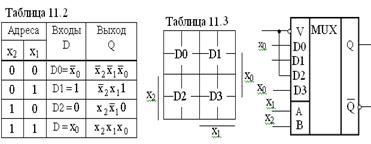
Рисунок 11.10 – Схемная реализация

При большом числе переменных (n ≥ 4) такой формализованный подход вряд ли оправдан, т.к. аппаратные затраты возрастают, а выигрыш необоснован. Более целесообразно в этих случаях синтез комбинационных на мультиплексорах производить с использованием элементов некоторого базиса, например, И, ИЛИ, НЕ и т.д.

В этом случае часть переменных n_адр используют в качестве адресов мультиплексора, остальные n – n_адр служат для формирования управляющих сигналов по информационным входам.

Пусть задана переключательная функция четырех переменных f(x₄x₃x₂x₁) в виде суммы суммы минтермов:

Если переменные x₄ x₃ будут являться адресами выбора входа мультиплексора, тогда карта Вейча для данной переключательной функции будет выглядеть, как показано в таблице 11.4.

Квадрат, описанный произведением 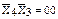, будет определять вход D0, 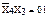– первый, 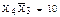– второй и 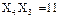– третий вход мультиплексора. Минимизация функции по каждому входу производится для каждого квадрата индивидуально. Анализ информации, расположенной в еречисленных квадратах, дает следующие результаты:

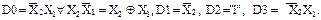
Схемная реализация этой функции приведена на рисунке 11.11

Минимизированное выражение для данной функции, полученное обычным образом, выглядит следующим образом: 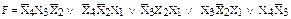. Для схемной реализации данного выражения требуется пять трехвходовых ЛЭ типа И (два корпуса К555ЛА4 – 3И-НЕ´3) и один корпус К555ЛА3 для реализации логического сложения. Сравнение ранее полученного решения с данным показывает, что первый вариант выигрывает по сравнению со вторым по числу используемых корпусов МСХ и сложности монтажа. Синтез комбинированных схем с пятью переменными x₅, x₄, x₃, x₂, x₁ можно вести на восьмивходовых мультиплексорах. В качестве адресных сигналов можно выбирать переменные x₅, x₄, x₃, а информационные сигналы формировать из переменных x₂, x₁. Рассмотрим пример схемной реализации переключательной функции, представленной в таблице 11.5, на восьмивходовом мультиплексоре. Адресные переменные x₅, x₄, x₃ задают номер квадрата, который соответствует такому же номеру информационного входа. Логическое выражение, описывающее функцию внутри каждого квадрата, определяет характер входного сигнала на данном входе. При диагональном расположении единиц описывающая функция является «равнозначностью» или «неравнозначностью» x₂ и x₁, одна «единица» в квадрате описывается логическим произведением входных переменных (x₂ x₁), а горизонтальное или вертикальное расположение двух «единиц» дает прямое или инверсное значение одной из входных переменных.

В результате анализа таблицы 11.5 получим следующие значения функций по входам мультиплексора:

D0 – Х₁ Å Х₂ ; D1 – Х₂ ; D2 – Х₁ ; D3 –U¹ ;

D4 – Х₁ Х₂ ; D5 – 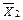; D6 – 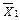; D7 – U⁰.

Реализация этой функции на восьмивходовом мультиплексоре приведена на рисунке 11.12.

Минимизированное выражение для данной переключательной функции, полученное традиционным способом, дает следующий результат:

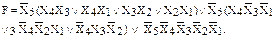
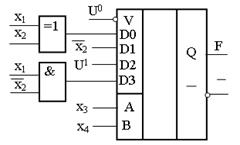
Рисунок 11.11 – Схемная реализация

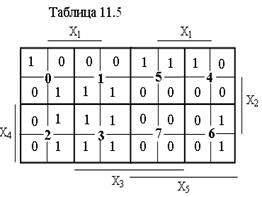
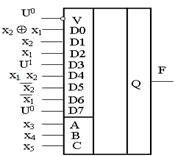
Рисунок 11.12 – Схемная реализация на восьмивходовом мультиплексоре

Релизация этого выражения на логических элементах типа И, ИЛИ, НЕ окажется весьма громоздкой. Сравнение полученных результатов показывает, что использование мультиплексоров для реализации логических функций во многих случаях оказывается оправданным.

12 АРИФМЕТИЧЕСКИЕ УСТРОЙСТВА

12.1 Комбинационные двоичные сумматоры

Сумматор – это узел, в котором выполняется арифметическая операция суммирования цифровых кодов двух двоичных чисел. Числа в любой позиционной системе счисления складываются поразрядно. Поэтому сложить двоичные числа можно при наличии узлов, реализующих суммирование цифр одного разряда слагаемых с учетом возможного переноса из соседнего младшего разряда. К таким узлам относят одноразрядные комбинационные полусумматоры и сумматоры.

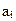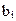Комбинационный полусумматор HS предназначен для суммирования двух одноразрядных двоичных чисел. Он имеет два входа , и , два выхода – S_i и P_i+1. Выход S_i является выходом суммы, а выход P_i+1 – выходом переноса.

На основании таблицы 12.1 переключательные функции для S_i, и P_i+1 в СДНФ будут иметь следующий вид:

Полусумма 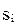является функцией неравнозначности входных сигналов 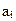и 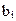(«исключающее ИЛИ» )

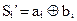, (12.1)

которая инверсна по отношению к функции равнозначности

. (12.2)

Таблица 12.1

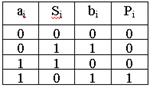
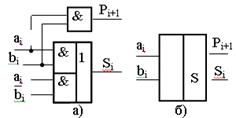
Рисунок 12.1 – Полусумматор: а − функциональная схема;

б − условное графическое изображение

Устройство можно реализовать на логических элементах И, ИЛИ (рисунок 12.1). Основным требованием, предъявляемым к нему, является получение максимального быстродействия при минимальном числе последовательно включенных элементов.

Одноразрядный комбинационный сумматор 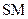предназначен для суммирования трех одноразрядных двоичных чисел. Он имеет три входа: 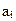, , 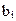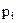и два выхода: S_i и P_i+1. На входы 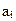и 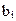поступают значения суммируемых цифр данного разряда, на вход 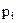– значение переноса из соседнего младшего разряда. Порядок переключения трехвходового сумматора представлен в таблице 12.2, условное графическое обозначение на рисунке 12.2. На основе таблицы истинности (таблица 12.2) переключательные функции в СДНФ для S_i и P_i+1 будут иметь следующий вид:

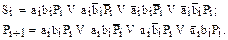
Таблица 12.2

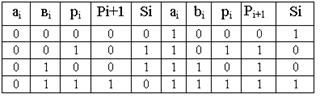
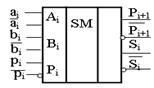
Рисунок 12.2 – Одноразрядный комбинационный сумматор

Минимизируем полученные выражения с помощью карт Карно (рисунок 12.3). Анализ таблицы для S_i показывает, что переключательная функция упрощению не поддается. Тогда преобразуем это выражение с помощью правил алгебры логики. Объединим первый и четвертый, второй и третий минтермы, а их общие сомножители (P_i и 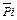) вынесем за скобки:

.

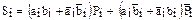С учетом (12.1) и (12.2) это выражение запишется в виде .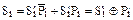

Оригинальное выражение для суммы S_i можно получить непосредственно из таблицы 12.2

.

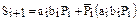Минимизированное логическое выражение для результата переноса в следующий разряд P_i+1 найдем по карте Карно:

P_i+1 = a_i b_i + a_i P_i + b_i P_i = a_i b_i + P_i (a_i + b_i).

Введем обозначения:

G_i = a_i b_i и T_i = (a_i + b_i),

получим

P_i+1 = G_i + P_i T_i.

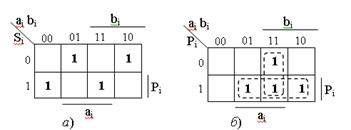
Рисунок 12.3 – Карты Карно: а − переключательных функций S_i; б − переключательных функцийP_i

Функцию G_i называют функцией генерации (формирования) поразрядного переноса i-го разряда, а T_i – функцией передачи (распространения) переноса для i- го разряда. Реализация устройства суммирования трехразрядного сумматора может выполняться как показано на рисунке 12.4.

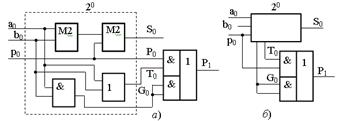
Рисунок 12.4 – Сумматор: а − одноразрядный сумматор; б− упрощенное изображение

МикросхемаК555ИМ5 – два одноразрядных полных сумматора. Она выполняет операцию сложения трех одноразрядных чисел в двоичном коде с учетом переноса младшего разряда в старший (рисунок 12.5).

Состояние выходных уровней схемы в зависимости от состояний на входах , 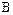и 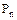соответствует показанным в таблице 12.2.

Высокий и низкий уровни сигнала на выходах схемы S_n и P_n+1 устанавливаются при наличии высокого и низкого уровней на всех входах микросхемы.

Рисунок 12.5 – Условное графическое изображение ИС К555ИМ5