Ступенчатые дешифраторы

Принцип построения ступенчатых дешифраторов рассмотрим на примере построения дешифратора 4х16. Переключательные функции полного дешифратора с высоким активным уровнем на выходе выглядят следующим образом:

, , , , , , , , , , , , , , , .

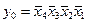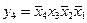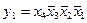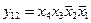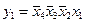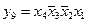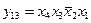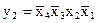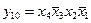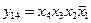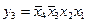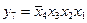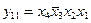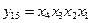Разобьем входные переменные x₄, x₃, x₂, x₁, весовые значения которых 8-4-2-1 соответственно, на пары: x₄, x₃ и x₂, x₁ (причем допускается любой другой вид разбивки).

Каждую пару переменных используем для построения двухвходового линейного дешифратора первой ступени преобразования. В результате получим:

, , , ,

, , , .

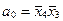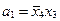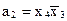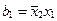Переменные y₀, y₁…,y₁₅ получим на второй ступени преобразования путем логического перемножения переменных a₀…,a₃ на b₀…,b₃:

, , , ,

, , , ,

, , , ,

, , , .

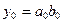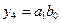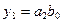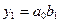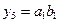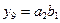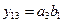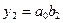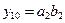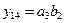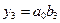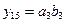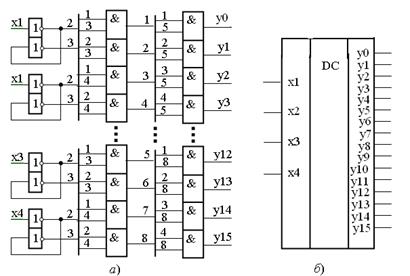
а − структурная схема; б −условное обозначение

Рисунок 10.2 – Ступенчатый дешифратор на четыре входа

На рисунке 10.2, а приведена функциональная схема двухступенчатого преобразователя, а на рисунке 10. 2, б его условное графическое изображение.

Функциональная схема содержит инверторы для переменных x₄,…,x₁, восемь двухвходовых ячеек И на первой ступени преобразования, 16 – во второй. Такую структуру преобразования иногда называют прямоугольной, а вторую ступень – матричным преобразователем.

Пирамидальные дешифраторы.Отличительной особенностью пирамидальной структуры построения дешифраторов является то, что на каждой ступени преобразования добавляется всего лишь одна переменная. Если входных переменных n, то число ступеней преобразования n – 1. Например, для четырехвходового дешифратора на первой ступени преобразования получим функции двух переменных а₀,…, а₃, как в ступенчатом дешифраторе. На второй ступени преобразования переменные а₀,…,а₃ перемножим с входом переменной 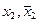и получим восемь промежуточных сигналов:

, , , ,

, , , .

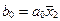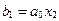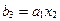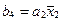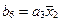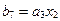На третьей, последней, ступени преобразования сигналы b₀,…,b₇ умножаются на переменную 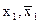, в результате чего оказываются сформированными все входные сигналы:

, , , ,…, ,

, , , ,…, .

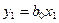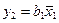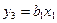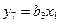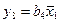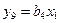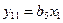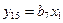Основным недостатком ступенчатых дешифраторов является увеличенная задержка распространения сигнала.

Формирование логических функций. Дешифраторы-демультиплексоры легко использовать для формирования логических функций, заданных таблицей истинности. В качестве примера рассмотрим реализацию переключательной функции трех аргументов, заданных таблицей 10.2. Cудя по таблице, входная функция представляет сумму пяти минтермов:

.

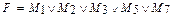Поскольку рассматриваемая функция зависит от трех аргументов, то она может быть реализована с помощью двоично-десятичного дешифратора 3:8. Учитывая, что дешифратор имеет инверсные выходы, а количество нулей в заданной выходной функции (три) меньше числа единиц (пять), целесообразно на выходе реализовать инверсную функцию (инверсию суммы нулей). По таблице нетрудно заключить, что

.

Следовательно, для реализации функции на выходе дешифратора необходимо установить логическую ячейку И, входы которой соединить с выходами У_{0 ,}У₄ и У₆ Функциональная схема устройства приведена на рисунке 10.3.

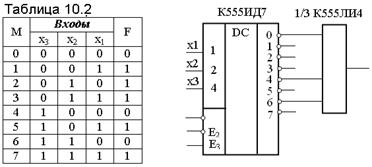
Рисунок 10.3 – Схемная

Реализация функции

Управляющие сигналы 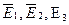связаны между собой конъюнктивно, и дешифратор переходит в активное состояние при Е₁ = 0, Е₂ = 0, Е₃ = 1. При любых других сочетаниях этих сигналов выходы дешифраторов переходят в неактивное состояние с высокими выходными уровнями напряжения. В том случае, когда число единиц в выходной функции меньше числа нулей, на выходе дешифратора предпочтительнее использовать логическую схему ИЛИ.