СХЕМЫ СРАВНЕНИЯ ЦИФРОВЫХ КОДОВ
13.1 Общие положения
Схемы сравнения кодов довольно часто встречаются в промышленных цифровых приборах, устройствах вычислительной техники, измерительных системах и служат для выявления соответствия некоторого значения цифрового кода заданному уровню. Схемы сравнения кодов условно можно разделить на две группы:
– выявляющие совпадение кодов;
– выявляющие большее число.
Схемы, выявляющие совпадения кодов, должны обеспечить выходной сигнал, равный единице, только в случае полного совпадения сравниваемых кодов. Сравниваться могут числа, заданные в двоичном и двоично-десятичном коде, имеющие одинаковое количество разрядов: А = Аn…А2А1А0, В = Вn…В2В1В0. Совпадение кодов означает равенство чисел во всех разрядах:
Аn = Вn, …, А2 = В2, А1 = В1, А0 = В0.
При сравнении двух одноразрядных кодов можно не составлять таблицу истинности, поскольку для совпадения кодов достаточно, чтобы оба разряда были равны нулю либо единице. Такую функцию реализует схема равнозначности:  = Аi º Вi, а ее инверсивное значение имеет функция неравнозначности («исключающее ИЛИ»):
= Аi º Вi, а ее инверсивное значение имеет функция неравнозначности («исключающее ИЛИ»): 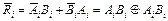 , т.е. сумма по модулю два.
, т.е. сумма по модулю два.
При равенстве кодов реализуется функция  …
…  , преобразуя которую по правилу де Моргана (отрицания), получим
, преобразуя которую по правилу де Моргана (отрицания), получим 

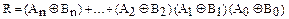 .
.
Последнее выражение можно реализовать с помощью логических схем «исключающее ИЛИ» и схемы ИЛИ (рисунок 13.1). За основу взята МСХ К133ЛП5 (555, 1531, 1533 и др.), содержащая четыре 2-х входовых элемента «исключающее ИЛИ» и 4-х входовой логический элемент ИЛИ-НЕ (половина ИС К155ЛЕ3). Логический элемент ИЛИ-НЕ имеет дополнительный вход разрешения приема сигнала EI (Enable Input). Управляющий сигнал на этом входе разрешает (или запрещает) прием сигнала по каждому входу ЛЭ.
Построение схемы, выявляющей большее (или меньшее) из двух сравниваемых чисел, рассмотрим на примере сравнения двух двоичных чисел А = Аn…А2А1А0, В = Вn…В2В1В0. Схема должна обеспечить на выходе сигнал N, равный единице в случае, когда A > B. Если же А £ В, то сигнал на выходе такой цепи должен быть равен нулю. Для получения логической функции, которую должна реализовать схема, нужно взять за основу ячейку, сравнивающую одноразрядные коды. При этом очевидно что Ai > Bi, если Ai =1 и Bi = 0, т.е. 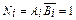 .
.
Многоразрядные числа следует сравнивать следующим образом. Вначале сравнивают коды в первом, старшем разряде. Если Аn > Bn, следовательно,  ,и сразу можно сделать вывод, что независимо от содержания младших разрядов
,и сразу можно сделать вывод, что независимо от содержания младших разрядов
А>В. Если же в первом разряде коды совпадают, то  и нужно перейти к анализу следующего разряда. Если в следующем разряде An–1>Bn–1, тогда
и нужно перейти к анализу следующего разряда. Если в следующем разряде An–1>Bn–1, тогда  1 и, следовательно, А>B. Если же в этом разряде An-1 = Bn-1, то с учетом равенства бит старшего разряда получим промежуточный результат:
1 и, следовательно, А>B. Если же в этом разряде An-1 = Bn-1, то с учетом равенства бит старшего разряда получим промежуточный результат:
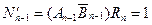 .
.
Рассуждая таким образом, получим:

 ;
;  ; …
; …
 ;
; 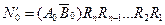 .
.

Рисунок 13.1 – Cхема cравнения кодов на равенство
Если хотя бы одно значение  окажется равным единице, то на выходе дизьюнктора
окажется равным единице, то на выходе дизьюнктора 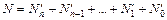 установится высокий уровень, указывающий на то, что А>В.
установится высокий уровень, указывающий на то, что А>В.
Сигналы Ri, полученные по ходу решения задачи,можно использовать для реализации функции R, указывающей на равенство кодов. Если буквой Мi обозначить функцию, принимающую уровень лог.1 при Аi < Вi (  ), то формулу для Ri можно записать в следующем виде:
), то формулу для Ri можно записать в следующем виде:
 .
.
Это означает, что Ri = 1 в том случае, когда ai = bi.
Реализовать устройство, выявляющее большее число, можно на ЛЭ низкой степени интеграции, хотя в этом нет необходимости, поскольку в разных сериях имеются цифровые четырехразрядные компараторы. Примером могут служить микросхемы К564ИП2, К555СП1, К531СП1 (ТТЛШ), выпускаемые отечественной промышленностью.

Рисунок 13.2 – Условное графическое обозначение
ИС К564ИП2
13.2 Цифровые компараторы и их применение
Цифровые компараторы 555, 531, 561, 564 серий в функциональном отношении близки друг к другу. Они определяют равенство или неравенство сравниваемых четырехразрядных чисел, имеют дополнительные входы для наращивания разрядности. На рисунке 13.2 приведено условное графическое обозначение ИС 564ИП2. Числа, подлежащие сравнению, подаются на входы А0 – А3 и В0 – В3 (А3 и В3 – старшие разряды). Результаты сравнения появляются на выходах А > В, А = В, А < В. Микросхема имеет расширяющие входы А < В, А = В, А > В, что позволяет наращивать разрядность сравниваемых чисел без привлечения дополнительных элементов. Если используется только один корпус ИП2, то на вход А = В необходимо подать высокий уровень, а на вход А > В и А < В – низкиеуровни.
При каскадировании микросхем входы расширения можно использовать для программирования выполняемых функций (таблица 13.1). Для удобства описания выполняемых функций введем следующие обозначения:
A = A3A2A1A0, B = B3B2B1B0 – входные двоичные слова;
f>, f=, f< – двоичный код на входах наращивания разрядности, соответственно, >, =, <.;
F>, F =, F< – сигналы на выходах микросхемы, соответственно, >, =, <.
Функции, реализуемые МСХ К564ИП2, запишутся в следующем виде:
F= = f= ´ F(A = B), F< = F(A < B) Ú f<´ F(A = B),
F> = f> [ F(A>B) Ú  ].
].
Функции программируются с помощью входов А > В, А = В, А < В (4, 6, 5) и соответствуют таблице программирования (таблица 13.1).
Таблица 13.1 – Таблица истинности К564ИП2
| ВХОДЫ | ВЫХОДЫ | ||||
| f>(A>) | f=(A) | f<(A<) | F> (A >В) | F =(A = B) | F<(A<B) |
| F(A <B) | |||||
| F(A£ B) | |||||
| F (A = B) | F(A< B) | ||||
| F (A = B) | F(A£ B) | ||||
| F (A ³ B) | F(A <B) | ||||
| F (A > B) | F (AB) | ||||
| F (A > B) | F (A = B) | F (A<B) | |||
| F(A > B) | F (A = B) | F(A£ B) |
На рисунке 13.3, а в качестве примера приведена схема преобразования разрядности сравниваемых чисел. На приведенном рисунке f> = 1, f= = 1, f< = 0. Подставив эти значения в вышеприведенные формулы, получим:
F= = F(А = В), F> = F(А > В), F< = F(А < В), F> ´ F< = 0.
Отсюда видно, что при таком управлении МСХ соотношения «меньше», «больше» и «равно» входных четырехразрядных чисел полностью переносятся на выходные функции F< и F>, которые можно рассматривать как выходные одноразрядные числа.
На рисунке 13.3 показана 8-ми разрядная схема сравнения двоичных чисел, построенная их двух 4-х разрядных ИС 561ИП2. На вход А> первой МСХ (сравнение младших разрядов числа) можно подавать либо низкий, либо высокий уровень напряжения. Сигнал переноса f0 > необходимо подать на вход А> второго компаратора. Из рисунка 13.3 следует, что
F8= = F4=×F(A2 = B2),
F8< = F(A2 < B2) V f4< × F(A2 = B2),
F8> = f0> × 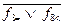 ,
,
A2 = A7 A6 A5 A4, B2 = B7 B6 B5 B4.
Таблица 13.1 – Таблица истинности К564ИП2
| ВХОДЫ | ВЫХОДЫ | ||||
| f>(A>) | f=(A) | f<(A<) | F> (A >В) | F =(A = B) | F<(A<B) |
| F(A <B) | |||||
| F(A£ B) | |||||
| F (A = B) | F(A< B) | ||||
| F (A = B) | F(A£ B) | ||||
| F (A ³ B) | F(A <B) | ||||
| F (A > B) | F (AB) | ||||
| F (A > B) | F (A = B) | F (A<B) | |||
| F(A > B) | F (A = B) | F(A£ B) |
Следовательно, функции, выполняемые схемой, соответствуют таблице 13.1.Можно построить схему последовательного включения большего числа ИС К561ИП2 для сравнения 4m-разрядных чисел, где m – число ИС. Сигналы f< и f= всегда подаются на младшую ИС, а сигнал f> – на старшую ИС (деление на младшие и старшие ИС производится в соответствии с младшими и старшими разрядами сравниваемых чисел). Входы A < B, A = B всех остальных МСХ следует соединить с одноименными выходами предыдущих, а на входы A > B подать лог. 1.
При последовательном включении ИС снижается быстродействие схем сравнения многоразрядных чисел (увеличивается задержка распространения сигнала), поэтому предпочтительнее параллельное (пирамидальное) соединение МСХ (рисунок 13.5). Интегральная МСХ К555СП1 (рисунок 13.4) выполняет функции сравнения 4-х разрядных двоичных чисел, но ее переключательные функции отличаются от ранее рассмотренных для К564ИП2.

а − четырехразрядных; б − восьмиразрядных
Рисунок 13.3 – Схемы сравнения разрядности чисел

Рисунок 13.4 − Цифровой компаратор двоичных чисел:
а − четырехразрядный компаратор ИС К555СП1; б − восьмиразрядный компаратор на двух ИС К555СП1
Переключательные функции описываются следующими выражениями: F4= = f= ´ F(А1 = В1),
 ,
,
 .
.
На рисунке 13.4 приведена 4-х разрядная схема и 8-ми разрядная схема сравнения двоичных чисел.
Нетрудно заметить, что наблюдается полная симметрия по отношению к операциям больше и меньше при каскадном наращивании разрядов. Функции, выполняемые ИС К555СП1, могут программироваться сигналами f0>, f0=, f0< (таблица 13.2).
Таблица 13.2 – Таблица истинности восьми разрядного
Компаратора
| ВХОДЫ | ВЫХОДЫ DD1 | ВЫХОДЫ DD2 | ||||||
| f0> | f0= | f0< | F4> | F4= | F4< | F8> | F8= | F8< |
| F(A³ B) | F(A£B) | F(A > B) | F(A<B) | |||||
| F(A> B) | F(A£ B) | F(A > B) | F(A£B) | |||||
| F(A> B) | F(A=B) | F(A< B) | F(A > B) | F(A=B) | F(A< ) | |||
| F(A> B) | F(A=B) | F(A< B) | F(A > B) | F(A=B) | F(A<B) | |||
| F(A³ B) | F(A< B) | F(A ³ B) | F(A<B) | |||||
| F(A> B) | F(A<B) | F(A ³ B) | F(A£B) | |||||
| F(A> B) | F(A=B) | F(A< B) | F(A > B) | F(A=B) | F(A<B) | |||
| F(A> B) | F(A=B) | F(A< B) | F(A > B) | F(A=B) | F(A<B) |
На рисунке 13.5 показана схема сравнения 24-разрядных двоичных чисел при параллельном включении ИС К555СП1. МСХ D2 – D5 используются для преобразования разрядности сравниваемых чисел, причем в качестве дополнительных входов используются входы наращивания разрядности A<, A>.
Соотношения «меньше», «больше» и «равно» выявляются между 5-разрядными числами A5 = ( а3 а2 а1 а0 f0.>) и В5 = (в3 в2 в1 в0 f0<) и полностью переносятся на выходные функции f4> и f4< (например, если A5 = B5, то f4> = f4<), которые можно рассматривать как 1-разрядные. Параллельное (пирамидальное) построение ифровых схем сравнения позволяет довести длину сравниваемых слов до 124 бит при небольших технических затратах (31 корпус ИС 555СП1). Задержка распространения сигнала будет не более 75 нс.

Рисунок 13.5 – Схема сравнения 24-разрядных двоичных чисел при параллельном включении ИС К555СП1
Дата добавления: 2020-03-17; просмотров: 2755;











