Визначення об’єму подовжнього укорочення
У відповідності з прийнятими вище припущеннями, розглянемо термомеханічну сторону задачі. Визначимо залишкові напруження, що виникають при наплавленні шва на пластину товщиною (Δ), у припущенні необмеженої жорсткості пластини і відсутності тепловіддачі. Як показує аналіз кінетики процесу, ці припущення справедливі, якщо середня температура поперечного перерізу не перевищує 100 0С, що забезпечується при qп/А≤400 Дж/см3, (qп - погонна енергія (Дж/см, А - площа перерізу стержня).
Виділимо з пластини елементарну смугу dx і поділимо її на призми шириною dy. Будемо вважати, що деформації кожної призми не залежать від деформацій сусідніх призм і визначаються тільки максимальною температурою на відстані у від осі шва (рисунок 3.1).
Будемо розглядати кожну призму як стержень, жорстко закріплений на торцях (рисунок 3.2). Як видно з рисунка 3.1 термомеханічний цикл для призми 1 приводить до появи пластичних деформацій стиску, вторинних пластичних деформацій і залишкових напружень розтягу, які дорівнюють границі текучості. У призмі 2 виникають пластичні деформації стиску, але напруження розтягу не перевищує границі текучості. По завершенні термічного циклу залишкові пластичні деформації визначаються заштрихованою площею АS на рисунку 3.1.
Величина площі визначається інтегралом:
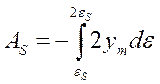 , (3.1)
, (3.1)
де ym - ординати кривої εТm=αTm.
Знак "мінус" в рівнянні (3.1) враховує, що залишкові пластичні деформації - від’ємні.
Згідно з (2.13), крива максимальних температур визначається залежністю:
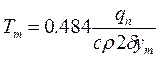 , (3.2)
, (3.2)
звідки ординати кривої температурних деформацій:
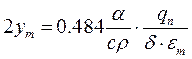 . (3.3)
. (3.3)
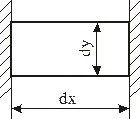
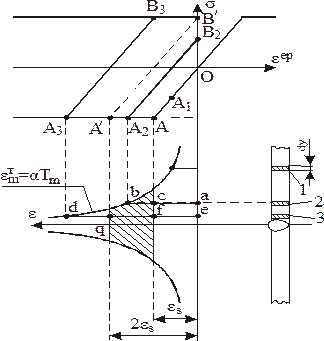
| Рисунок 3.1– Напружено-деформований стан виділених призм | Рисунок 3.2 –Схема закріплення призми |
Після підстановки (3.3) у (3.1) і інтегрування, одержимо:
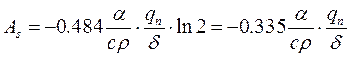 . (3.4)
. (3.4)
Об’єм поздовжніх пластичних деформацій стиску (об’єм подовжнього укорочення) визначається формулою:
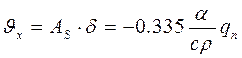 . (3.5)
. (3.5)
Дата добавления: 2020-03-17; просмотров: 880;











