Комплексные числа и действия над ними.
Система действительных чисел является неполной, так как не содержит корни некоторых многочленов, например 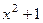 . Если квадратичное уравнение
. Если квадратичное уравнение 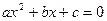 имеет отрицательный дискриминант, то есть
имеет отрицательный дискриминант, то есть 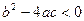 , то на действительной оси нет ни одного корня. Однако существует система условных, обобщённых чисел, где и такие уравнения тоже имеют решения. Они называются комплексными числами и геометрически соответствуют точкам на плоскости, а известная ранее действительная ось - это горизонтальная ось Ох в данной плоскости. Введено абстрактное понятие «мнимая единица»
, то на действительной оси нет ни одного корня. Однако существует система условных, обобщённых чисел, где и такие уравнения тоже имеют решения. Они называются комплексными числами и геометрически соответствуют точкам на плоскости, а известная ранее действительная ось - это горизонтальная ось Ох в данной плоскости. Введено абстрактное понятие «мнимая единица» 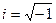 обозначающая «квадратный корень из минус 1». При этом получается
обозначающая «квадратный корень из минус 1». При этом получается 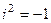 .
.
Геометрическая интерпретация. На плоскости, горизонтальная ось отождествляется со множеством действительных чисел, а мнимая ось, содержащая 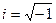 , перпендикулярна оси действительных чисел.
, перпендикулярна оси действительных чисел.
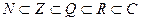 .
.
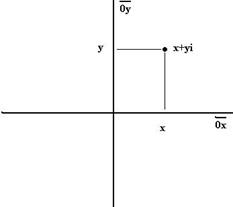
Комплексные числа - ещё более абстрактное обобщение. Оно полезно при решении различных физических задач. Плоскость комплексных чисел есть расширение множества действительных чисел. Каждой точке на плоскости с координатами 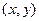 можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части:
можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части: 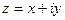 . Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа.
. Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа. 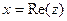 ,
, 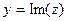 .
.
Если 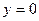 , то число
, то число 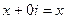 это обычное действительное число.
это обычное действительное число.
Сложение и вычитание комплексных чисел определяется покоординатно, как для обычных векторов в плоскости.
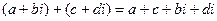 =
= 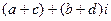 .
.
Для вычитания аналогично: 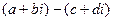 =
= 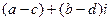 .
.
Умножение.
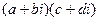 =
= 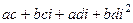 , учитывая тот факт, что
, учитывая тот факт, что 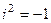 ,
,
получаем 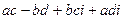 =
= 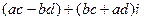 .
.
Таким образом, после раскрытия скобок, надо просто учесть 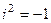 и привести подобные.
и привести подобные.
Пример. 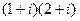 =
= 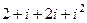 =
= 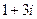 .
.
Определение. число 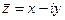 называется сопряжённым к
называется сопряжённым к 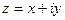 .
.
Умножим два взаимно сопряжённых комплексных числа:
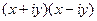 =
= 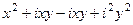 =
= 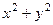 , получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0. Этот факт можно использовать для процедуры деления. Если домножить на сопряжённое в знаменателе, то там получится действительное число, и это даст возможность разбить на сумму двух дробей. При этом, конечно, в числителе тоже домножаем на сопряжённое к знаменателю, чтобы дробь не изменилась.
, получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0. Этот факт можно использовать для процедуры деления. Если домножить на сопряжённое в знаменателе, то там получится действительное число, и это даст возможность разбить на сумму двух дробей. При этом, конечно, в числителе тоже домножаем на сопряжённое к знаменателю, чтобы дробь не изменилась.
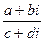 =
= 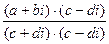 =
= 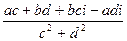 =
= 
Пример. Вычислить 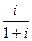 .
.
Решение. 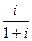 =
= 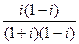 =
= 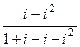 =
= 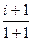 =
= 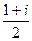 =
= 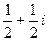
Дата добавления: 2020-03-17; просмотров: 746;











