Цель: научиться определять множества, отношения между ними, выполнять операции над множествами.
Определение 1:Множество представляет собой соединение, совокупность, собрание некоторых предметов, объединённых по какому-либо признаку.
Обозначается А;B;C … или 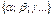 , где
, где 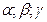 -элементы множества.
-элементы множества.
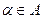 означает ”элемент
означает ”элемент 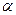 принадлежит множеству А.”
принадлежит множеству А.”
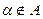 означает ”элемент
означает ”элемент 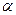 не принадлежит множеству А.”
не принадлежит множеству А.”
Например: 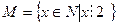 означает ”М-это множество натуральных чисел x таких, что каждое из них делится нацело на 2.”
означает ”М-это множество натуральных чисел x таких, что каждое из них делится нацело на 2.”
Определение2: Множества А и В называют равными, если они состоят из одних и тех же элементов.
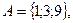
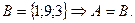
Определение3: Если любой элемент множества В является и элементом множества А, то множество В называют подмножеством множества А. Говорят, что множество В содержится в А 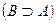 или множество А содержит множество В
или множество А содержит множество В 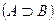 .
.
Определение4: Пустое множество- множество не содержащее ни одного элемента.
Обозначается : 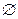 .
.
Теорема: Пустое множество является подмножеством любого множества.
Определение 5: Степенью множества А называется множество всех подмножеств множества А.
Обозначается : 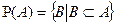
Например: 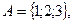 тогда P(А)=
тогда P(А)= 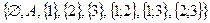
Теорема: Число элементов множества P(А) равно 2n, где n-число элементов множества А.
Например: для 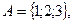 число элементов P(А) равно 23=8.
число элементов P(А) равно 23=8.
Свойства множеств.
1. 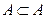 (любое множество является своим подмножеством.)
(любое множество является своим подмножеством.)
2. если А 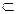 В, В
В, В 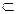 Z, то А
Z, то А 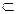 Z;
Z;
3. если А 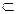 В, В
В, В 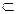 А, то А=В
А, то А=В
Операции над множествами.
1) Объединением или суммой двух множеств А и В называется множество, состоящее из элементов, которые принадлежат или множеству А или множеству В: А 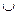 В={
В={ 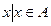 или
или 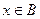 }. Например: А={1;2;8}, В={3;1}, тогда А
}. Например: А={1;2;8}, В={3;1}, тогда А 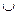 В={1;2;3;8}.
В={1;2;3;8}.

A B
А 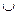 В
В
2)  Пересечением или произведением 2-х множеств А и В называется множество, состоящее из тех элементов, которые принадлежат и множеству А и множеству В: А
Пересечением или произведением 2-х множеств А и В называется множество, состоящее из тех элементов, которые принадлежат и множеству А и множеству В: А 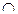 В={
В={ 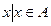 и
и 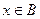 }. Например: А={1;2;8}, В={3;1}, тогда А
}. Например: А={1;2;8}, В={3;1}, тогда А 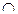 В={1}.
В={1}.
A 



 B
B
А 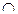 В
В
Определение 6: Если А  В=
В= 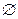 , то множества А и В называются непересекающимися.
, то множества А и В называются непересекающимися.
3) Разностью множеств А и В называется множество, которое состоит из всех элементов множества А не принадлежащих множеству В:А\В={ 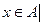
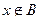 }. Например: А={1;2;8}, В={3;1}, тогда А\В={2;8}.
}. Например: А={1;2;8}, В={3;1}, тогда А\В={2;8}.
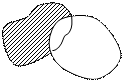
A B
A\B
Определение 7: Если А 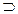 В, то разность А\В называется дополнением множества P до множества.
В, то разность А\В называется дополнением множества P до множества.
Основные формулы алгебры множеств.
1) 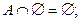
2) 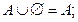
3) 
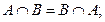
4) 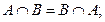 коммутативность;
коммутативность;
5) 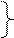
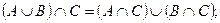
6) 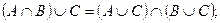 дистрибутивность;
дистрибутивность;
7) 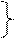
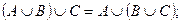
8) 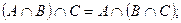 ассоциативность.
ассоциативность.
Практическая часть.
1) Найти все элементы множества Е= 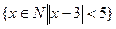
Решение: найдём решение неравенства 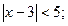
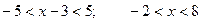 или
или 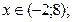
выберем из полученного решения 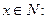
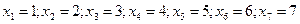 .
.
Таким образом 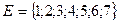
2) Найти а)множества А целых чисел, удовлетворяющих неравенству 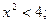 б)все подмножества найденного множества А; в) число элементов степени множества А.
б)все подмножества найденного множества А; в) число элементов степени множества А.
Решение: найдём решение неравенства 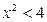 :
: 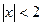 или
или 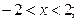 выберем целые числа
выберем целые числа 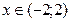 , т.е.
, т.е.
- А={-1;0;1};
- определим степень множества А, т.е. все подмножества А Р(А)={ 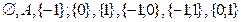 };
};
- число элементов множества Р(А) равно 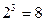
3) Даны множества: А={-4;-3;-2;-1;0;1;2},
В={3;4;2;1;0;-1;-2},
С={-4;-3;-2;-1;0;1;2;3;4}.
Найти 1) объединение (дизъюнкцию) множеств А и В;
2) пересечение (конъюнкцию) множеств В и С;
3) разность множеств С и А;
4) дополнение множества А до С ;
5) А  В
В  С;
С;
6) А 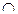 В
В 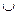 С;
С;
7) (А\В) 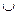 (В\С);
(В\С);
Решение:
1) согласно (1) А 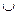 В={-4;-3;-2;-1;0;1;2;3;4}=С.
В={-4;-3;-2;-1;0;1;2;3;4}=С.
2) согласно (2) B 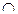 C={-2;-1;0;1;2;3;4}.
C={-2;-1;0;1;2;3;4}.
3) согласно (3) C\A={4;3}.
4) дополнение множества А до С : M={3;4}.
5) (A 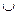 B)
B) 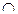 C={-4;-3;-2;-1;0;1;2;3;4}=C; C
C={-4;-3;-2;-1;0;1;2;3;4}=C; C 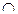 C=C.
C=C.
6) (A 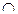 B)
B) 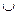 C={-4;-3;-2;-1;0;1;2;3;4}; A
C={-4;-3;-2;-1;0;1;2;3;4}; A 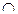 B={-2;-1;0;1;2}.
B={-2;-1;0;1;2}.
7) A\B={-4;-3}; B\C= 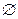 ; (A\B)
; (A\B)  (B\C)={-4;-3}.
(B\C)={-4;-3}.
Дата добавления: 2020-03-17; просмотров: 557;











