Тема: «Решение однородных обыкновенных дифференциальных уравнений первого порядка и линейных обыкновенных дифференциальных уравнений первого порядка»

Цель: научиться решать дифференциальные уравнения с разделяющимися переменными, линейные I порядка.

I Основные понятия

О1:ДУ I-го порядка связывают независимую переменную х, искомую функцию y и её производную :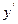

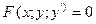(1)

Если уравнение (1) можно разрешить относительно 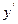, то его записывают в виде:

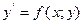
О2: Общим решением ДУ I-го порядка называется функция 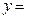j(х; с); содержащая одну производную постоянную и удовлетворяющая условиям:

1) функция j(х; с) является решением ДУ при каждом фиксированном с;

2) для любого начального условия 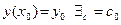такое, что функция 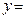j(х; с₀) удовлетворяют данному начальному условию.

О3: Частным решением ДУ I-го порядка называется любая функция

у = j(х; с₀), полученная из общего решения у=j(х;с) при конкретном значении постоянном с=с_0.

II ДУ с разделяющимися переменными

Общий вид ДУ: 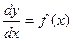^*j(у) (2)

Или Р₁(х)Q₁(у)dx + Р₂(х)Q₂(у)dy = 0

Метод решения :

В уравнении 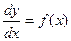^*j(у) разделяем переменные: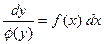

Интегрируем обе части равенства: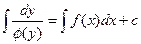

III Однородные ДУ I-го порядка

Общий вид: у^’=f(x; y) удовлетворяет условию f(x;y) = f(lx; ly)

Метод решения: решаем заменой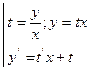

IV Линейные ДУ

Общий вид: у^’+p(x)y=q(x), где p(x), q(x) – заданные функции (3)

Метод решения: Решение ищется в виде произведения двух функций:

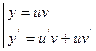(4)

Ход решения: Подставляем соотношение (4) в уравнение (3):

u^’v + uv^’ + p(x)uv = q(x),

u^’v + u[v^’ + p(x)v] = q(x),

Пусть v такое, что [] = 0

v^’ + p(x)v = 0,

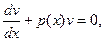
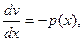
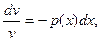
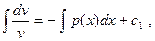
ln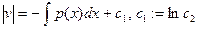

ln ,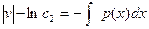

,

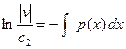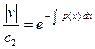
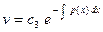, c₃=1

Итак:

v =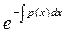

Подставим v в уравнение (5)

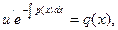
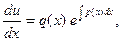
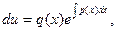
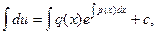
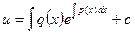
Т.к. 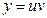, то y=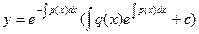

Замечание: уравнение Бернулли

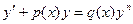
решается с помощью той же замены (4)