Тема: «Нахождение производных и дифференциалов высших порядков»
Цель: научиться дифференцировать различные функции одной переменной.
Производной функции y=f(x) называется предел отношения приращения функции 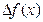 к приращению аргумента
к приращению аргумента 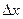 , когда
, когда 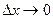 ; обозначается
; обозначается 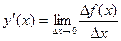 или
или 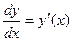 .
.
Правила дифференцирования
1. (u 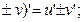 2.
2. 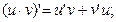 3.
3. 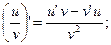 4.
4. 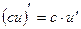 , где
, где 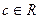 .
.
Формулы дифференцирования
1. 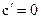 ;
;
2. 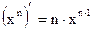 ;
;
3. 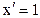 ;
;
4. 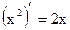 ;
;
5. 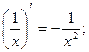
6. 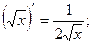
7. 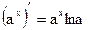 ;
;
8. 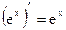 ;
;
9. 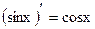 ;
;
10. 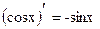 ;
;
11. 
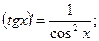
12. 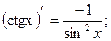
13. 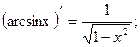
14. 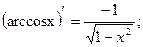
15. 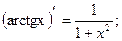
16. 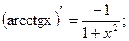
17.
Производной функции II порядка называется производная от производной I порядка этой функции; обозначается 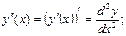
Физический смысл производной:
1. Производная от функции пути определяет скорость в любой момент времени 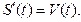
2. Производная от функции скорости определяет ускорение в любой момент времени 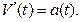
3. Вторая производная от функции пути определяет ускорение в любой момент времени 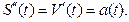
Производная сложной функции 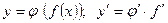
Производная параметрически заданной функции:
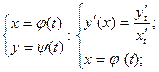
Практическая часть.
Найти производные заданных функций.
1. 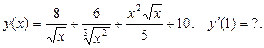
Преобразуем функцию к виду удобному для дифференцирования:
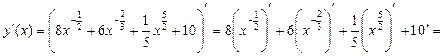
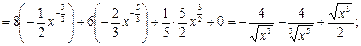
Найдём 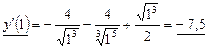

Преобразуем функцию 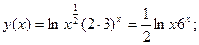
Найдём
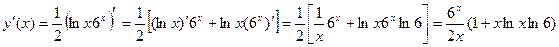
Найдём:
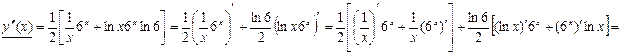
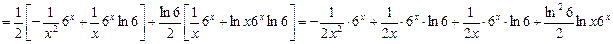
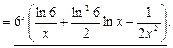
2. 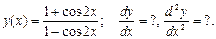
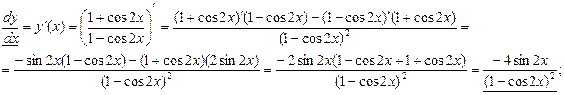
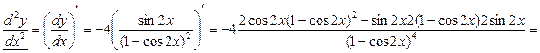
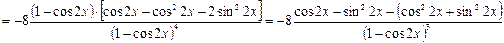
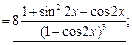
3. 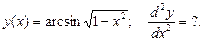
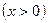
Найдём 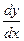 , используя формулу произвольной сложной функции:
, используя формулу произвольной сложной функции:
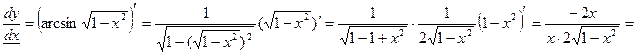
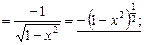
4. 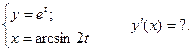
Найдём 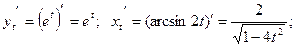
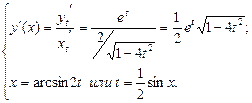
Тема: “Нахождение неопределённых и определённых интегралов различными методами “
Дата добавления: 2020-03-17; просмотров: 538;











