Тема: ” Числовые и степенные ряды. Применение степенных рядов к приближенным вычислениям значений функции”.
Цель: исследовать данные ряды на сходимость.
Числовые ряды
О: Числовым рядом называют выражение вида 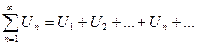 , где
, где 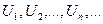 -члены ряда; Un –общий член ряда.
-члены ряда; Un –общий член ряда.
I. Схема исследования на сходимость положительных числовых рядов.
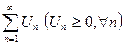
 |
- Выписать 3 первых члена ряда.
- Проверить выполнение необходимого условия сходимости (н.у.с.) ряда, т.е.
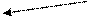
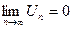
НУС выполненоНУС не выполнено
Продолжить исследования, Вывод: ряд расходится
Применив один из трёх признаков:
- признак сравнения
- признак Коши
- признак Даламбера
 |
Сделать вывод.
Т1: (признак сравнения) пусть ряды (1) 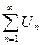 и (2)
и (2) 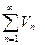 - положительные и
- положительные и 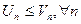
Тогда 1) если ряд (1) расходится, то ряд (2)-расходиться.
2) если ряд (2) сходится, то ряд (1)-сходиться.
Т2: (признак сравнения) пусть ряды (1) 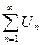 и (2)
и (2) 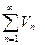 - положительные и существует
- положительные и существует 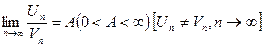 , тогда ряды (1) и (2) сходятся и расходятся одновременно.
, тогда ряды (1) и (2) сходятся и расходятся одновременно.
Замечание.
1) Удобно ввести сравнение с гармоническим рядом.
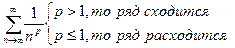
2) Формулы эквивалентности:
а) 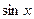 ~arcsinx~arctgx~ex-1~ln(x+1)~x,
~arcsinx~arctgx~ex-1~ln(x+1)~x, 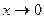
б) ax-1~xlna, 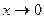
в) loga(1+x)~ 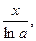
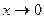
3) ”шкала роста функций”
ln n <<en<<n!<<nn, 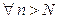
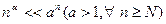
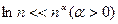 (*)
(*)
Т3: (признак Коши) Пусть ряд 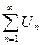 -положительный и
-положительный и 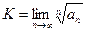 . Тогда:
. Тогда:
- Если К>1, то ряд расходится.
- Если К<1, то ряд сходится.
- Если К=1, то необходимы дополнительные исследования.
Т4: (признак Даламбера) Пусть ряд 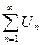 положительный и
положительный и 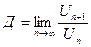 . Тогда:
. Тогда:
- Если Д<1, то ряд сходится.
- Если Д>1, то ряд расходится.
- Если Д=1, то необходимы дополнительные исследования.
II. Схема исследования знакочередующихся рядов.
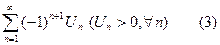
 |
- выписать 3-4 первых члена ряда.
-

 исследовать на абсолютную сходимость. Составить ряд из модулей
исследовать на абсолютную сходимость. Составить ряд из модулей 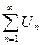 (4) и исследовать его на сходимость (см. схему исследования I.).
(4) и исследовать его на сходимость (см. схему исследования I.).
(4) сходится(4) расходится
Вывод: (3) сходится абсолютно Вывод для ряда (3)
нет абсолютной сходимости
 |
исследовать ряд (3) на условную сходимость, применив признак Лейбница
Т5: (признак Лейбница) Ряд 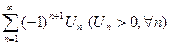 сходится, если:
сходится, если:
1. 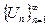 монотонно убывает, т.е.
монотонно убывает, т.е. 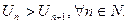
2. 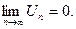
Дата добавления: 2020-03-17; просмотров: 628;











