Практическая часть.

Пример 1.

Исследовать на сходимость положительный ряд.

А)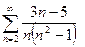

Решение.

Обратимся к схеме (I).

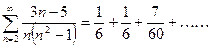
Проверим выполнение н.у.с.

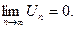
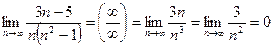, т.е. н.у.с. выполнимо.

Продолжим исследование, применив признак сравнения (Т2).

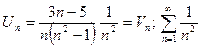сходится, т.к. это гармонический ряд (р=2>1) I 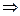данный ряд сходится.

Б)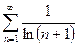

Решение:

обратимся к схеме I.

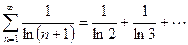
Проверим выполнение н.у.с.

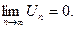
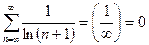, т.е. н.у.с. выполнилось.

Продолжим исследование, применив признак сравнения (Т1).

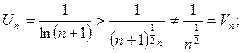
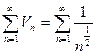расходится как гармонический ряд с р=1/2<1 данный ряд расходится.

В)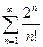

Решение:

Обратимся к схеме I.

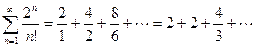
Т.к. проверка н.у.с.

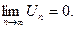
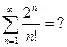вызывает затруднение, то применим достаточный признак сравнения числового ряда, а именно признак Даламбера.

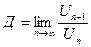
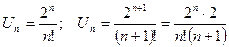
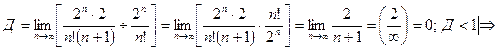ряд сходится.

Пример 2. Исследовать ряд на условную и абсолютную сходимость.

А)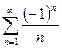

Решение: обратимся к схеме II.

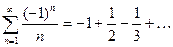
Исследуем ряд на абсолютную сходимость. Составим ряд из модулей.

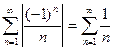- расходится как гармонический с р=1.

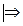для данного ряда нет абсолютной сходимости.

Исследуем ряд на условную сходимость. Применим признак Лейбница:

1) ;

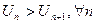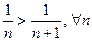
2)

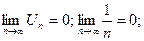
Т.к. условия признака Лейбница выполнены, то данный ряд сходится условно.

Пример 3. Найти радиус сходимости и интервал сходимости степенного ряда.

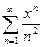
Решение: Обратимся к схеме III: т.к. 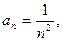то

1)

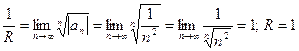
2) Интервал сходимости ряда:

сходится

расходится расходится

-1 0 1 х

(-R;R)=(-1;1)

3) Исследуем сходимость ряда в точках x=-1 и х=1:

х=1

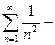сходится как гармонический с р=2>1.

х=-1

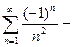сходится абсолютно.

Ответ: R=1; интервал сходимости [-1;1]