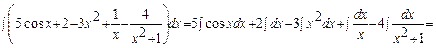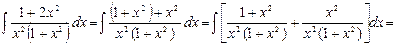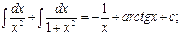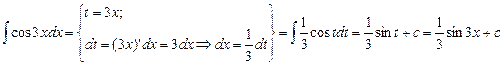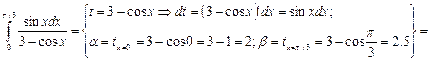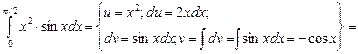Цель: научиться интегрировать функции различными методами, а так же вычислять определённые интегралы.
Неопределённым интегралом от функции 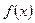 называется совокупность первообразных для этой функции;
называется совокупность первообразных для этой функции;
Обозначается: 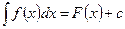 , где
, где 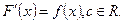
Свойства неопределённого интеграла:
-
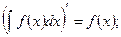 4.
4. 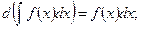
-
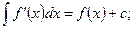 5.
5. 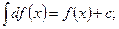
-
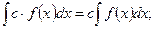 6.
6. 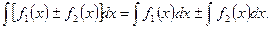
Методы вычисления:
1. Непосредственный (с помощью формул и свойств).
2. Метод замены переменной (вводится подстановка 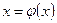 или
или 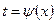 ).
).
3. Метод по частям (используется формула 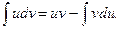 ).
).
Основные формулы интегрирования:
1. 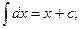
2. 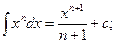
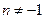
3. 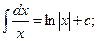
4. 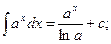
5. 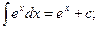
6. 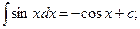
7. 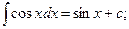
8. 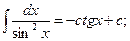
9. 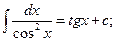
10. 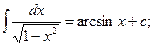
11. 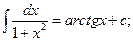
12. 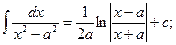
13. 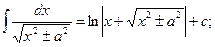
14. 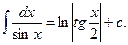
Определённым интегралом от функции 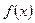 на отрезке
на отрезке 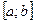 называется предел интегральной суммы функции
называется предел интегральной суммы функции 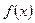 при достаточно мелком разбиении
при достаточно мелком разбиении 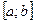
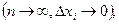
Обозначается: 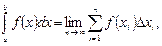 , где а – верхний, b – нижний предел интегрирования.
, где а – верхний, b – нижний предел интегрирования.
Свойства определённого интеграла:
1. 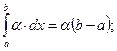
2. 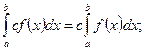
3. 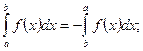
4. 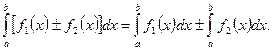
Методы вычисления:
- непосредственный (с помощью свойств и формулы Ньютона-Лейбница:
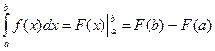 );
); - метод подстановки (
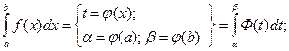
- метод интегрирования по частям (используется формула
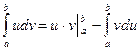
Практическая часть
Найти интегралы:
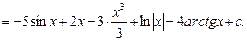
4. 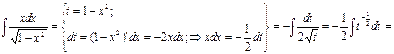
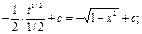
-
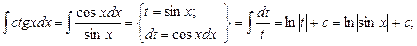
-
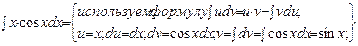 =
= 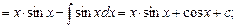
-
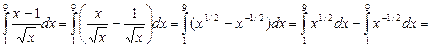
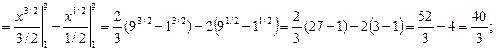
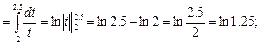
= 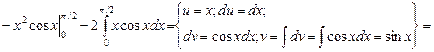
= 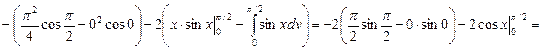
= 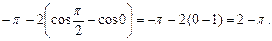
Тема: ”Действия над комплексными числами, заданными в алгебраическом виде. Умножение и деление комплексных чисел в тригонометрической форме”
Цель: научиться выполнять действия над комплексными числами, изображать их
Определение: Комплексными числами называются числа вида z=x+iy, где x;y 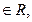 а число i, определяемое равенством i2=-1, называется мнимой единицей, если для этих чисел выполняются условия:
а число i, определяемое равенством i2=-1, называется мнимой единицей, если для этих чисел выполняются условия:
z1=x1+iy1, z2=x2+iy2.
1) z1=z2 ó 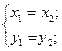
2) z1+z2=(x1+x2)+i(y1+y2);
3) 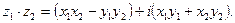
Множество комплексных чисел обозначается С.
* Запись z=x+iy называется алгебраической формой записи комплексных чисел.
x=Rez – действительная часть комплексных чисел.
y=Jmz-мнимая часть комплексных чисел.
Любое действительное число содержится во множестве комплексных чисел: x=2 ó z=2+ 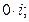 т.е. R
т.е. R 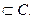
Числа вида 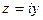 (или
(или 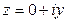 ) называют чисто мнимыми к.ч.
) называют чисто мнимыми к.ч.
Число 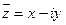 называются сопряжённым числу
называются сопряжённым числу 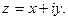
Числа 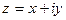 и
и 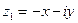 - противоположные к.ч.
- противоположные к.ч.
Геометрически к.ч. изображаются либо точками (x;y), либо радиус-векторами точек (x;y) на комплексной координатной плоскости (х – действительная ось, у – мнимая ось).
Длина радиус-вектора точки (x;y) называется
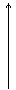 y модулем к.ч., обозначается
y модулем к.ч., обозначается 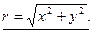


 y z=x+iy Угол, образованный радиус вектором и
y z=x+iy Угол, образованный радиус вектором и
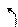 r
r 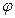 положительным направлением действительной оси
положительным направлением действительной оси
 0 называется аргументом к.ч. и обозначается
0 называется аргументом к.ч. и обозначается
x x 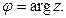
Если точка (x;y) находится:
в I четверти, то 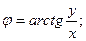
в II четверти, то 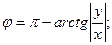
в III четверти, то 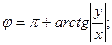
в IV четверти, то 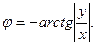
Например:
1.  z=1-i; y так как (1;-1)
z=1-i; y так как (1;-1) 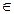 IV четверти, то
IV четверти, то






 0 1 х
0 1 х 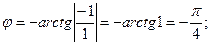
-1
 y
y
2. z=-2; , 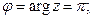
-2 0 x
3. 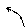


 z=3i; y ,
z=3i; y , 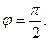
o x
I. Действия над к.ч. в алгебраической форме: 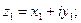
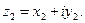
1) Сложение 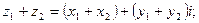
2) Вычитание 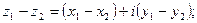
3) Умножение 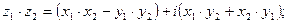
4) Деление 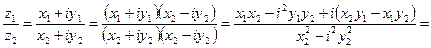
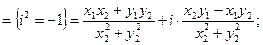
5) Возведение в степень (формула Муавра): 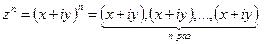
6) Извлечение корня из n-й степени 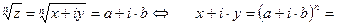
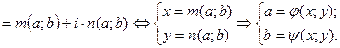
* Тригонометрическая форма записи комплексных чисел имеет вид z=r 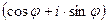
Например: z=-2+2i; r= 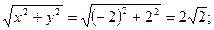
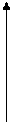 y
y 




 2
2 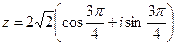
-2 x
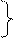 II. Действия над к.ч.в тригонометрической форме.
II. Действия над к.ч.в тригонометрической форме.
1)Сложение удобней выполнять в алгебраической форме
2)Вычитание
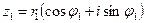
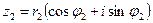
3)Умножение 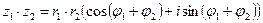
4)Деление 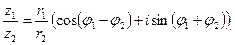
5)Возведение в степень 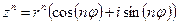
6)Извлечение корня n-й степени
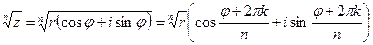 , где k=0;1;2;…n-1.
, где k=0;1;2;…n-1.
* Показательная форма записи к.ч. 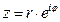
III. Действия над к.ч. в показательной форме.
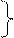 1)Сложение удобней выполнять в алгебраической форме
1)Сложение удобней выполнять в алгебраической форме
2)Вычитание
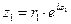
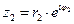
3)Умножение 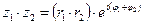
4)Деление 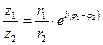
5)Возведение в степень 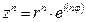
6)Извлечение корня n-й степени 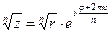 , где k=0;1;…,n-1.
, где k=0;1;…,n-1.
Практическая часть
1) Найти модуль и аргумент числа 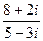
*Выполним деление согласно правилу I.4) :
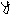
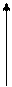
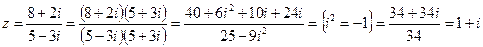


 Найдём модуль к.ч. z :
Найдём модуль к.ч. z : 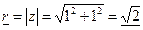 и аргумент к.ч. z 1 z=1+i
и аргумент к.ч. z 1 z=1+i

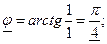 (
( 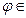 I четверти). 0 1 х
I четверти). 0 1 х
2)Выполнить действия 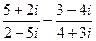 и результат представить в показательной форме.
и результат представить в показательной форме.
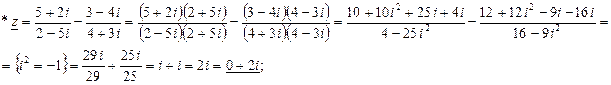

 Найдём модуль r=
Найдём модуль r= 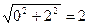 и аргумент
и аргумент 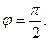 y
y

 Запишем z в показательной форме z=2
Запишем z в показательной форме z=2 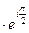
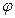 x
x
3) Возвести в степень по формуле Муавра 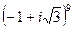 .
.
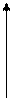 *Найдём модуль и аргумент числа
*Найдём модуль и аргумент числа 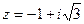 у
у





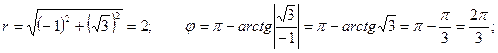
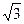
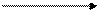 Запишем число в тригонометрической форме:
Запишем число в тригонометрической форме: 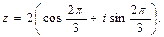 -1 0 х
-1 0 х
Возведём число z 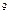 согласно формуле Муавра II.5)
согласно формуле Муавра II.5)
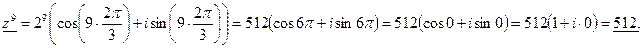 y
y

 0 512 x
0 512 x
4) Решить уравнения :
а) 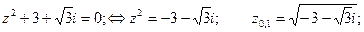
Представим число 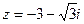 в показательной форме:
в показательной форме: 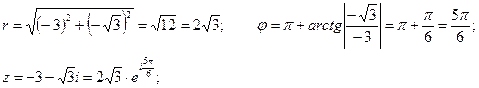
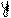
 Извлечём
Извлечём 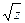 согласно формуле III.6)
согласно формуле III.6)





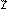
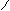
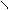
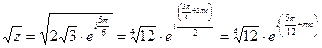 , где k=0;1.
, где k=0;1.
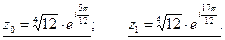
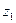
б) 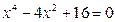
Пусть 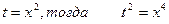 и данное уравнение примет вид
и данное уравнение примет вид 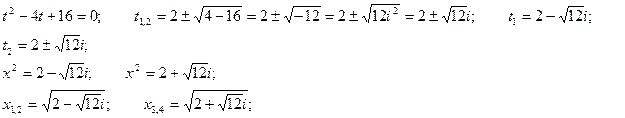
Найдём модули и аргументы чисел 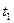 и
и 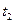 :
:

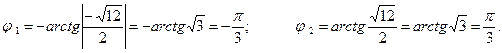
Запишем числа 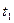 и
и 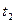 в показательной форме
в показательной форме
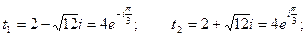
Извлечём 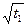 и
и 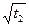 согласно правилу III.6)
согласно правилу III.6)
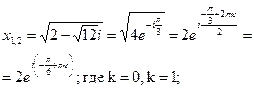
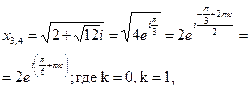
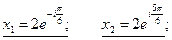
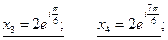
(k=0;) (k=1;) (k=0;) (k=1;)

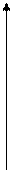 y
y




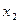
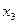
0 2 x
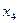
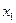
Дата добавления: 2020-03-17; просмотров: 706;