Определитель квадратной матрицы.

О: Определителем (детерминантом) квадратной матрицы А называется число

DА (det. А, |А|), которое находится по правилу:

1)

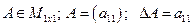
2) ;

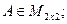
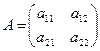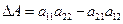
3)

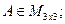
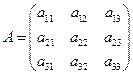
Определитель вычисляется по правилу Саррюса:

⊕ · · · · · · ⊖

· · · · · ·

· · · · · ·

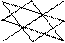
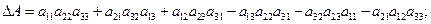
4) Общее правило вычисления определителей.

Определитель любого порядка можно вычислить, выполнив разложение по какой-нибудь строке или столбцу (удобно раскладывать по строке или столбцу содержащим нули),

т. е.

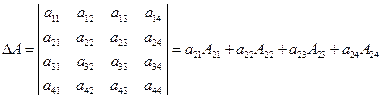
(разложение выполнено по второй строке), где 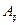– алгебраическое дополнение элемента 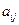, вычисляемое по правилу: .

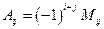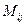(минор матрицы А) определитель матрицы, полученный из исходной, вычёркиванием 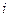-той строки и 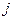-ого столбца.

Т. е.

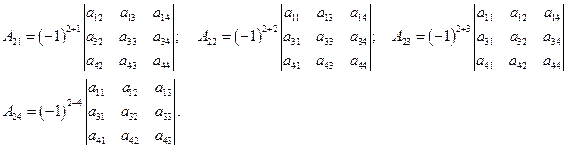
СЛАУ

О: Систему вида

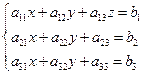(1)

будем называть системой трёх уравнений с тремя неизвестными x, y и z.

Введём в рассмотрение следующие матрицы

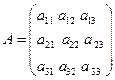
– матрица, составленная из коэффициентов системы (1).

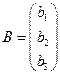
– матрица-столбец свободных членов системы (1).

О: Упорядоченная тройка чисел (x₀, y₀, z₀), при подстановке которой в систему (1) каждое уравнение обращается в верное равенство называется решением СЛАУ (1).