Методы поиска обратной матрицы.

1. С помощью алгебраических дополнений, по формуле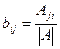

- уже рассмотрено выше. Но есть и другие методы.

2. С помощью элементарных преобразований.Если матрицу А привести к виду Е, то при синхронно выполненных элементарных преобразованиях на месте Е будет обратная.

Пример.Найти обратную матрицу для .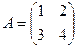

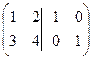
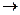
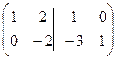
(из 2 строки вычли утроенную 1-ю, получили треугольную матрицу)

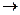
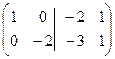(к 1-й строке прибавили 2-ю, получили диагональную матрицу)

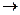
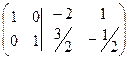(поделили 2-ю строку на ).

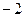Слева получили Е, справа А^-1 .

С помощью решения систем уравнений.

Например, матричное уравнение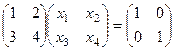

распадается на два уравнения:

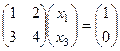и .

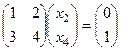Что приводит к системам уравнени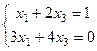й:

и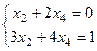

Решение первой из них 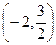, второй .

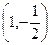Ранг матрицы.

Для прямоугольных матриц не существует понятие определителя, однако там можно выбирать квадратные подматрицы, и для них определитель вычислить можно. Если задать какие-нибудь k номеров строк и k номеров столбцов, то на пересечениях, очевидно, получится минор из k² элементов. Он может быть вырожденным либо нет. Существует минор максимального порядка, который является невырожденным. Его порядок и называется рангом матрицы.

Определение. Порядок наибольшего невырожденного минора называется рангом матрицы.

Обозначается 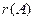. Примеры:

Матрица размера 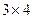ранга 2. 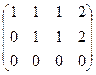. Здесь есть невырожденный минор порядка 2,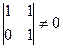

.

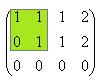Миноры 3 порядка можно рассматривать не все, достаточно только окаймляющие,то есть содержащие уже найденный минор меньшего порядка.

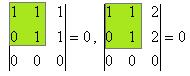
поэтому ранг не равен 3, а остаётся равен 2, так как минор 2 порядка уже найден. Миноров 4 порядка в этой матрице нет, так как всего 3 строки. Итак, 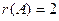. Цветом закрашен базисный минор.

А вот если в правом нижнем углу будет не 0, а 1, то ранг такой матрицы станет равен 3:

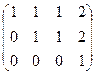
ведь теперь найдётся минор 3-го порядка, отличный от нуля:

Метод окаймлящих миноров (почему достаточно рассмотреть только их). Если, напр, 4 вектора образут систему ранга 2. Первые 2 из них линейно-независимы. Достаточно проверить системы, состоящие из 1,2,3 и 1,2,4 вектора. Если про 3-й вектор известно, что он лежит в плоскости 1-го и 2-го, и то же самое про 4-й, то все 4 в одной плоскости. Нет необходимости рассматривать системы из 1,3,4 или 2,3,4 векторов.

Ещё некоторые свойства ранга:

1) .

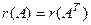2) Для прямоугольной матрицы размера : .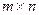

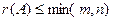Причина: минор более высокого порядка в этой матрице не существует, ведь размер вписанного квадрата не может превышать ни длину, ни ширину прямоугольника, в который вписан этот квадрат.

3) Если поменять местами 2 строки (столбца), то ранг не изменится.

4) Если умножить строку (столбец) на число, ранг не изменится.

Det умножается на k (не равный 0), свойство быть равным 0 или отличным от 0 не меняется.

(доказательства разобрать устно).

5) Элементарные преобразования, которые не меняют det.

(прибавить к строке другую, домноженную на k, отличный от 0).

Пример. Матрица ранга 1. Здесь 2 строка пропорциональна 1-й, а третья вообще нулевая:

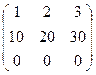
Матрица А является матрицей ранга 0 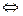она состоит только из нулей(очевидно, что если в матрице есть хоть один элемент, не равный 0, то он уже является минором 1 порядка, то есть ранг не 0, а уже 1).

Базисный минор порядка 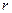может быть не единственным, их может быть и несколько. Так, например, в матрице:

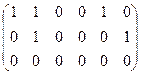
мы видим по крайней мере 2 различных минора порядка 2.