Цифровая фильтрация.

После АЦП используют процедуры обработки и фильтрации (для уменьшения шумов и дрейфов). Подбирать требуемый тип цифрового фильтра можно с использованием пакетов программ Мат Лаб (Mathlab) Мат Кад (Mathcad), LabView и др. По этому приведем лишь общие понятия, позволяющие ориентироваться в характеристиках цифровой фильтрации.

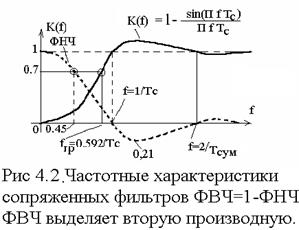5.1 Типовые параметры фильтров.

Параметрами являются граничные частоты полос пропускания и задержания (подавления), степень подавления, тип фильтра, допустимая неравномерность в полосе пропускания. Находится отклик фильтра, он однозначно связана с частотной характеристикой. При увеличении порядка отклика растет загрузка ЭВМ (время счета) и увеличивается задержка сигнала. Длительность отклика фильтра примерно равна τ = 1/∆F, где ∆F – полоса частот пропускания (по уровню 0,7). Это соотношение слабо зависит от типа используемого фильтра. (Для фильтра с характеристикой гауссова вида соотношение τ =1/∆F выполняется точно).

Следует еще привести общее соотношение между частотными характеристиками ФВЧ и ФНЧ: ФВЧ = 1 – ФНЧ_д, где ФНЧ_д – дополняющий фильтр низких частот. Это соотношение позволяет просто находить отклики ФВЧ как разность между входным сигналом и откликом ФНЧ_д, который имеет более простой вид. Приведенное соотношение не противоречиво, если 1 представить как ехр(jωτ), где τ есть время задержки фильтра. На рис 5.1представлены частотные характеристики сопряженных фильтров (для ФНЧ с прямоугольным откликом).

Эквивалентом фильтрации во временной области является операция свертки входного сигнала с откликом выбранного фильтра:

U(t)_вых = ∫ U_вх(τ)O_ф(t -τ)dτ,

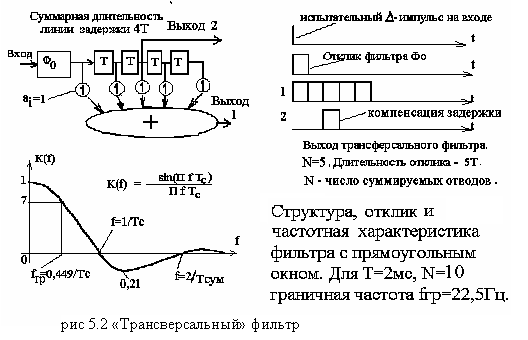
где U_вых(t)-выходной сигнал, U_вх(τ) – входной сигнал, O_ф(t- τ) – отклик фильтра, сдвинутый во времени на τ. Программа МатЛаб использует для нахождение выходного сигнала фильтра именно операцию свертки. Удобно при выборе фильтра выбирать не вид частотной характеристики, а форму его отклика. Общий вид преобразований с использованием откликов хорошо иллюстрируется при рассмотрении «трансверсального» фильтра рис 5.2.Такты ЭВМ заменены набором линий задержек. Весовые коэффициенты а_i определяют форму отклика (на рисунке они выбраны единичными), и хорошо понятен выход 2 - времени задержки фильтра. Полное значение числа отводов (или тактов) фильтра называется базой N или окном фильтра . На базе формируется весовая функция отклика. Задержка цифрового фильтра равна половине базы N. Формы весовых функций разнообразны, но если выделяется ее центральная часть с величинами, близкими к 1 (например с уровнем ≥ 0.7), то можно приближенно оценить полосу пропускания ΔF такого фильтра: ΔF ≈ 1/N_0,72T,

где N_0,7 - число отводов с весами, близкими к 1, а Т - период взятия выборки АЦП. Форма весовой функции вне центральной части определяет поведение частотной характеристики в полосе задержания. Если все весовые коэффициенты а_N заменить на коэффициенты (1-а_N),то получим сопряженный фильтр: ФВЧ вместо ФНЧ и наоборот (Рис 5.1.).

Переход в область реального времени от программы производится через величину τшага программы (выраженного во времени), что наглядно иллюстрируется "трансверсальным" фильтром. Структуры простейшего цифрового RC фильтра представлены в приложении.

6. Необходимые элементы математического анализа.

Интерполяция, аппроксимация, частотная фильтрация, распознавание, надежность процедуры распознавания с использование теории вероятности.

Когда возникли ЭВМ, достижения математиков стали доступны всем инженерам. По этому студентам надо знать важнейшие практические достижения в этой области.