Задачи фильтрации и методы ее реализации

Сигнал, несущий полезное сообщение, принимаемый в аддитивной смеси со случайной помехой, сам является случайным сигналом. Отсюда возникает проблема оптимального выделения случайного сигнала на фоне случайной помехи. Эта проблема распадается на ряд частных задач в зависимости от требований приложений результатов обработки. Можно определить наиболее характерные задачи фильтрации.

1. В силу ограниченности времени наблюдения в процессе обработки принимаемого колебания (смеси) находится не сам полезный сигнал, а его оценка, при этом ставится задача нахождения формы полезного сигнала с минимальными искажениями полезного случайного сигнала s(t).

Мерой качества фильтрации при этом может служить средний по множеству реализаций квадрат отклонения оценки сигнала 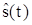, полученный на выходе системы обработки (фильтра), от истинной формы полезного сигнала, т.е. дисперсия оценки:

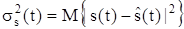. (5.24)

Критерием оптимальности отвечает минимизация оценки .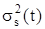

Относительно располагаемых реализаций случайного полезного сигнала можно различить два случая: а) наблюдения фиксированной длительности Т, когда обрабатываемое колебание задано (записано) на фиксированном отрезке [0,T], при этом возможно его многократное воспроизведение для обработки (встречается в условиях научного эксперимента, в разведке и т.д., б) текущее наблюдение, когда оценка полезного сигнала осуществляется в реальном текущем времени [0,t].

Кроме того, возможна в некоторых приложениях ситуация, когда отыскивается оценка на интервале времени, не совпадающем с интервалом наблюдения, т.е. при наблюдении процесса y(t) = s + n находится оценка 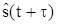, когда τ = 0, то решается задача текущей фильтрации, при τ > 0 – задача фильтрации с упреждением (предсказанием) или задача экстраполяции, при τ < 0 – задача фильтрации с запаздыванием или задача интерполяции (сглаживания).

2. При необходимости определения только наличия или отсутствия сигнала наилучшим критерием оптимальности фильтрации, а значит и постановки задачи фильтрации, является отыскание максимального отношения сигнал/помеха. Эта задача имеет самое широкое применение в системах связи, передачи информации.

При обсуждении вопросов фильтрации различают два ее вида: линейную и нелинейную фильтрацию.

При линейной фильтрации сигналы претерпевают только линейные преобразования: усиление, суммирование, дифференцирование, интегрирование. Процессы в линейной фильтрации описываются линейными дифференциальными уравнениями, имеется линейная связь между изменениями входного и выходного сигналов и справедливость принципа суперпозиции. Эти свойства присущие только линейным цепям, упрощают как реализацию, так и математическое описание линейных фильтров, что привело к выделению их в самостоятельный класс фильтров, получивших широкое применение.

Понятно, что, ограничиваясь применением только линейных фильтров, мы существенно снижаем свои возможности, т.к. в иных случаях нелинейная фильтрация может быть более оптимальной и дать лучший результат.

При нелинейной фильтрации осуществляются нелинейные преобразования сигналов (перемножение, возведение в степень и др.). Выходной сигнал нелинейного фильтра, в общем случае, определяется нелинейным дифференциальным уравнением.

Нелинейная обработка сигналов в ряде случаев позволяет получить более высокие показатели качества обработки, чем линейная, а иногда является единственно возможной формой обработки сигналов. Например, в случае, когда информационными параметрами являются фаза или частота сигнала, в силу нелинейной зависимости реализации сигнала от фильтруемого параметра может использоваться только нелинейная фильтрация. При этом оптимальными оказываются следящие фильтры (устройства фазовой или частотной автоподстройки частоты).

Литература:

[1] стр. 208-209. [2] стр. 180. [3] стр. 174.

Контрольные вопросы:

1. В чем заключается задача фильтрации сигнала?

2. Какие задачи решают оптимальные фильтры?

3. Как определяется оптимальность фильтра?

4. В чем разница между линейной и нелинейной фильтрацией?

5.10.2. Оптимальная линейная фильтрация по критерию
максимума отношения сигнал/шум (согласованные фильтры)

Комплексный спектр полезного сигнала

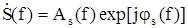. (5.25)

Обозначим передаточную функцию оптимального фильтра, обеспечивающего максимальное отношение сигнал/шум на выходе фильтра в некоторый момент времени t₀

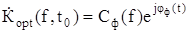. (5.26)

Значения отдельных спектральных составляющих полезного сигнала s(t) в момент t₀:

.

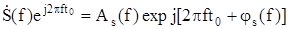Из физических соображений очевидно, что оптимальная фазочастотная характеристика фильтра φ_ф(t) соответствует сведению к нулю в момент t₀ фаз всех спектральных составляющих полезного сигнала на выходе фильтра. В этом случае обеспечивается максимальное значение выходного сигнала, поскольку все спектральные составляющие суммируются с одинаковой фазой, т.е. их амплитуды просто складываются.

,

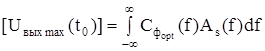для этого 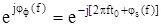, т.е.

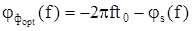. (5.27)

Дисперсия шума не зависит от фазочастотной характеристики фильтра, т.к. определяется энергетическим спектром на выходе фильтра, который не зависит от фазы спектральных составляющих.

Для определения амплитудно-частотной характеристики фильтра 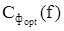, максимизирующей отношение мощностей сигнала и шума на его выходе в момент t₀, оценим вклад в каждую из этих мощностей элементарных участков спектра df.

Вклад участка спектра сигнала df в величину U_выхmax(t₀) равен:

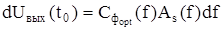
и соответствующий вклад в выходную мощность полезного сигнала:

dP_sвых .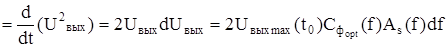

Выходная мощность шума, приходящаяся на участок спектра df:

dP_nвых .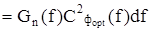

Отношение 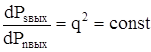по всей полосе частот и тогда

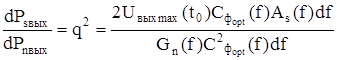
отсюда

.

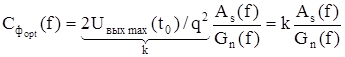Опуская несущественный масштабный коэффициент k, получаем выражение для комплексной характеристики оптимального фильтра:

,

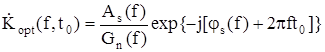
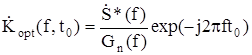где S*(f) – комплексный сопряженный спектр сигнала.

В случае, когда на выходе белый шум и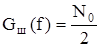

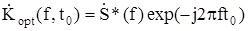. (5.28)

Таким образом, фильтр должен быть согласован (комплексно сопряжен) со спектром полезного сигнала (сомножитель 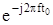не влияет на форму выходного сигнала, а только определяет задержку t₀ момента достижения максимума). Такие фильтры получили название согласованных или оптимальных линейных фильтров.

Определим максимальное отношение сигнал/шум на выходе согласованного фильтра 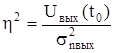при действии белого шума.

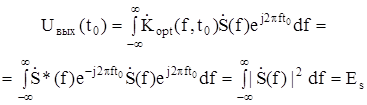
E_s – энергия полезного сигнала.

или для прямоугольного импульса E_s = A² × τ_u.

Средняя мощность шума на выходе фильтра:

.

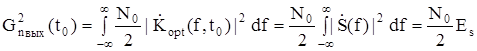При оценке энергии шума в полосе от -∞ до +∞ спектральная плотность выражается .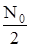

Тогда отношение по мощности:

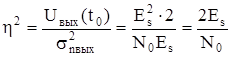. (5.29)

По напряжению отношения сигнал/шум будет:

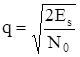. (5.30)

Это результат для белого шума (5.28), если шум не белый, то:

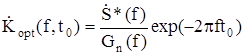. (5.31)

Отсюда видно, что для обработки смеси необходимо небелый шум привести к белому, произвести "отбеливание" шума.

Рис. 5.8

Рассмотрим для примера согласованный фильтр для сигнала вида прямоугольного видеоимпульса.

.

Спектральный состав видеоимпульса:

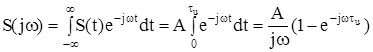. (5.32)

Комплексно-сопряженный спектр S*(jω) получаем при замене знака перед j:

.

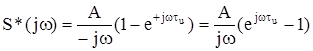Определим частотную характеристику согласованного фильтра в соответствии с выражением (5.28):

.

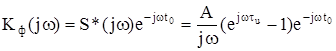Последний сомножитель определяет задержку t₀, которая означает, что искомое максимальное отношение сигнал/шум наступает только в момент t₀. Считая, что энергия сигнала существует во время от 0 до τ_u (далее она равна нулю), принимаем величину задержки отсчета на выходе фильтра равной длительности импульса, т.е. t₀ = τ_u, тогда

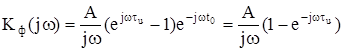. (5.33)

Получена комплексная частотная характеристика, в которой

А – амплитудное значение импульса;

1/jω – отражает частотную характеристику интеграла;

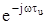- представляет задержку на τ_u.

Структурная схема согласованного с видеоимпульсом фильтра будет:

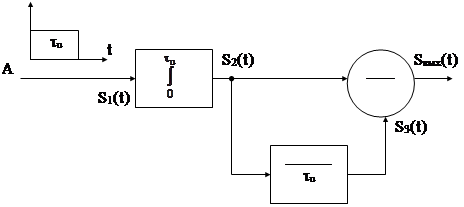Рис. 5.9

Действующее напряжение в схеме:

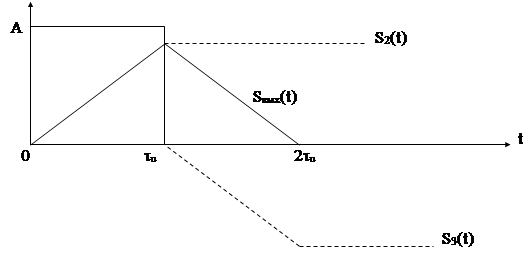
Рис. 5.10

При этом оказывается, что искаженная форма выходного сигнала имеет общую длительность в 2τ_u, максимальное значение выходного сигнала достигается в точке t₀ = τ_u. В этот момент на выходе фильтра отношение сигнал/шум будет максимальным именно в этот момент времени следует произвести отсчет сигнала на выходе фильтра.

Вместе с тем, спектральный состав видеоимпульса можно получить и в иной форме (см. лекцию 1):

S(jω) = A sin(ωτ_u/2). (5.34)

Разделив комплексный спектр на амплитудно-частотный и фазово-частотный получим графики (рис. 5.11)

Рис. 5.11

Литература:

[1] стр. 208-214. [2] стр. 180-186. [3] стр. 174-181.

Контрольные вопросы:

1. Почему согласованный фильтр называют оптимальным?

2. Почему оптимальный фильтр называют согласованным?

3. Какая форма сигнала на выходе согласованного фильтра?

4. Чему равно отношение сигнал/шум на выходе согласованного фильтра?