Критерий оптимальности Котельникова
Во многих каналах связи ошибки всех родов одинаково вредны. В этом случае в выражении (5.15) цены за ошибки a и b логично принять равными. Тогда правило решения (5.15) может быть упрощено следующим образом:
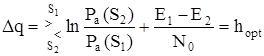 . (5.16)
. (5.16)
Выражение (5.16) и является правилом решения по критерию оптимальности Котельникова. Данный критерий был выдвинут академиком Котельниковым как часть теории систем связи, т.к. в период его разработки радиотехника сводилась, в основном, к системам связи, а такие ее разделы, как радиолокация, телеуправление и другие только зарождались.
Из выражения (5.15) и (5.16) следует, что критерий Котельникова можно считать частным случаем критерия Байеса.
Применительно к критерию Котельникова в выражении (5.11) можно, не снижая общности рассуждений, цены за ошибки a и b принять равными единице (a = b = 1). При этом функция риска примет следующий вид:
z = Pош(S1) + Pош(S2).
Таким образом, в критерии оптимальности Котельникова функция риска имеет следующий смысл: функция риска равна суммарной вероятности всех возможных ошибок. Следовательно, при обработке принятой смеси сигнала и помехи по правилу, соответствующему критерию Котельникова, минимизируется суммарная вероятность ошибок.
Данный критерий иногда называют также критерием максимума апостериорной вероятности. Действительно, в соответствии с выражением (5.3) и с учетом соотношения a = b = 1 правило решения может быть переписано так:
Pa(S1) l(S1) / Pa(S2) l(S2) = Pps(S1) / Pps(S2) 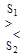 1. (5.17)
1. (5.17)
Следовательно, в соответствии с критерием Котельникова принимается решение о приеме того сигнала, который в результате обработки принятой смеси оказывается наиболее вероятным, т.е. апостериорная вероятность которого является максимальной.
Литература:
[1] стр. 170-173. [2] стр. 169-173. [3] стр. 163-168.
Контрольные вопросы:
1. В чем суть критерия оптимальности Байеса?
2. Чем отличается критерий Котельникова от критерия Байеса?
3. Что такое оптимальный порог?
Дата добавления: 2016-06-18; просмотров: 2673;











