Критерий оптимальности Байеса

Введем в рассмотрение следующую функцию вероятностей ошибок, называемую функцией потерь или функцией риска:

z = aP_ош(S₁) + bP_ош(S₂) = a P_a(S₂) P(S₁/S₂) + b P_a(S₁) P(S₂/S₁). (5.11)

Здесь a и b - коэффициенты, характеризующие цену потерь при ошибках соответствующих родов.

Оптимальной по критерию Байеса является такая обработка, которая минимизирует функцию риска. Определим правило решения, соответствующее критерию Байеса. Выразим функцию риска через функции правдоподобия. Выбор правила решения сводится к такому разбиению пространства решений на две непересекающиеся области, при котором функция риска является минимальной. Обозначим буквой А область, при попадании в которую принятой смеси y(t), принимается решение о приеме сигнала S₁(t), а буквой В - область, при попадании в которую принимается решение о приеме сигнала S₂(t). Тогда функцию риска можно выразить следующим образом:

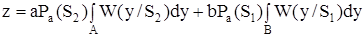, (5.12)

но 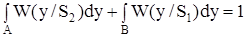, откуда

.

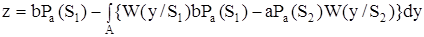Очевидно, что функция z достигает минимума при таком определении области А, при котором значение интеграла достигает максимума, максимум интеграла, в свою очередь, имеет место при условии, что в область А будут включены все положительные значения подынтегральной функции. Итак, область А определяется следующим условием:

,

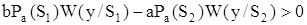откуда

l(S₁) / l(S₂) = W(y/S₁) / W(y/S₂) > aP_a(S₂) / bP_a(S₁).

Аналогично область В описывается так:

l(S₁) / l(S₂) < aP_a(S₂) / bP_a(S₁).

Если принятая смесь y(t) принадлежит области А, по принятому условию, должно приниматься решение о приеме сигнала S₁, при принадлежности к области В - о приеме сигнала S₂. В итоге правило решения, соответствующее критерию Байеса, может быть записано следующим образом:

l(S₁) / l(S₂) 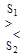aP_a(S₂) / bP_a(S₁). (5.13)

При помехе в виде аддитивного белого шума можно воспользоваться выражением (5.9) для отношения правдоподобия и записать правило решения следующим образом:

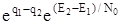
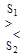aP_a(S₂) / bP_a(S₁). (5.14)

Т.к. отношение правдоподобия есть экспоненциальная, следовательно, монотонная функция аргументов q₁ и q₂, неравенства можно упростить, прологарифмировав левую и правую части неравенств (5.14). При этом правило решения преобразуется к следующему виду:

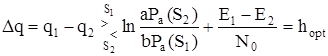. (5.15)

Выражение (5.15) в литературе часто называет функцией решения. Выражение в правой части неравенства известно и постоянно (все входящие в него элементы определяются), поэтому вычисляют как число и называют порогом сравнения – h.