Тема 9: СЛУЧАЙНЫЕ СИГНАЛЫ
Нет ничего более противного разуму и постоянству природы, чем случайность. Сам бог не может знать того, что произойдет случайно. Ибо если знает, то это определенно произойдет, а если определенно произойдет, то не случайно.
Цицерон. О девинации. (Римский философ)
Случайность противна нашему разуму, но не природе и богам. Именно для проверки теории случайных процессов боги и создали мир. Швыряться яблоками они уже перестали, со времен Ньютона в этом процессе ничего нового не наблюдалось. Но арбузные корки продолжают подсовывать - фиксируется непредсказуемая и зачастую очень даже интересная реакция.
Рудольф Гавшин. O cлучайном. (Уральский геофизик)
Содержание: 9.1. Случайные процессы и функции. Случайный процесс. Функции математического ожидания и дисперсии. Ковариационная функция. Корреляционные функции. Свойства функций автокорреляции и автоковариации. Взаимные моменты случайных процессов. Классификация случайных процессов. 9.2. Функции спектральной плотности. Каноническое разложение случайных функций. Комплексные случайные функции. Финитное преобразование Фурье. Спектр функций случайных процессов. Взаимные спектральные функции. Теорема Винера-Хинчина. 9.3. Преобразования случайных функций. Системы преобразования случайных функций. Математическое ожидание выходного сигнала. Ковариационная функция выходного сигнала. Функция взаимной ковариации входного и выходного сигналов. Спектральные соотношения. Дисперсия выходного сигнала. Функция когерентности. Преобразования случайных функций. Преобразования стационарных случайных функций. 9.4. Модели случайных сигналов и помех. Телеграфный сигнал. Белый шум. Гауссовский шум. Гауссовские случайные процессы. Литература.
9.1. Случайные процессы и функции [л31,л2,л4].
Теория вероятностей рассматривает случайные величины и их характеристики в "статике". Задачи описания и изучения случайных сигналов "в динамике", как отображения случайных явлений, развивающихся во времени или по любой другой переменной - координате, решает теория случайных процессов.
Как было принято и выше, в качестве универсальной координаты для распределения случайных величин по какой-либо независимой переменной будем использовать, как правило, переменную "t" и трактовать ее, чисто для удобства, как временную координату. Случайные распределения во времени обычно называют случайными или стохастическими процессами.
Случайный процесс Х(t) может быть описан функциональной системой случайных величин Хn = Х(tn), n = 1,2, … ,N при N Þ ¥ (соответственно Dt Þ 0), которая отличается тем, что принимаемые ею значения по координате t являются случайными. При регистрации случайного сигнала на определенном временном интервале осуществляется фиксирование единичной реализации xk(t) - выборочной функции случайного процесса X(t). С практической точки зрения эту выборочную функцию можно считать результатом отдельного эксперимента. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(xn;tn). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.
Одномерная плотность вероятностей p(x,t) случайного процесса Х(t) характеризует распределение вероятностей реализации случайной величины Х в произвольный момент времени t. Моменты времени ti, по существу, являются сечениями случайного процесса по пространству возможных состояний и плотность вероятностей p(x,t) представляет собой плотность вероятностей случайных величин Xi данных сечений. Однако одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.
Двумерная плотность вероятностей p(x1,x2;t1,t2) определяет вероятность совместной реализации значений случайных величин Х1 и Х2 в произвольные моменты времени t1 и t2 и в какой-то мере уже позволяет оценивать динамику развития процесса.
Случайные процессы и их функции характеризуются неслучайными функциями математического ожидания (среднего значения), дисперсии и ковариации:
Функции математического ожидания и дисперсиипредставляют собой соответственно математическое ожидание и дисперсию случайных величин по сечениям реализаций случайных процессов в произвольные моменты времени t:
mx(t) º M{Х(t)}º 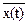 =
= 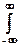 x p(x;t) dx, (9.1.1)
x p(x;t) dx, (9.1.1)
Dx(t) = M{[Х(t)-mx(t)]2} = 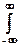 [xo(t)]2 p(x;t) dx, (9.1.2)
[xo(t)]2 p(x;t) dx, (9.1.2)
xo(t) = x(t)-mx(t).
Соответственно, функция среднего квадратического отклонения:
sx(t) = 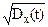 , (9.1.3)
, (9.1.3)
Математическое ожидание mx(t) называют также неслучайной составляющей случайного процесса X(t), а разность Х(t)-mx(t) - флюктуационной частью процесса. Пример неслучайной составляющей M{A(x)} случайного процесса А(х) можно видеть на рис. 9.1.3.
Ковариационная функция характеризует случайный процесс в целом.
На рис. 9.1.1 приведены примеры реализаций двух случайных процессов, которые характеризуются одной и той же функцией математического ожидания и дисперсии.
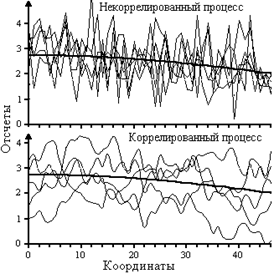 Рис. 9.1.1. Рис. 9.1.1.
|
На рисунке видно, что хотя пространство состояний обоих процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, а в пределе, во всех сечениях оба процесса могут иметь один и тот же закон распределения случайных величин. Однако динамика развития по координате t (или любой другой независимой переменной) единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, а, следовательно, в коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t1 и t2 задается функцией ковариации:
RХ(t1,t2) = M{Х(t1)Х(t2)}= 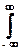
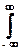 x(t1)x(t2) p(x1,t1;x2,t2) dx1dx2, (9.1.4)
x(t1)x(t2) p(x1,t1;x2,t2) dx1dx2, (9.1.4)
При анализе случайных процессов второй момент времени t2 удобно задавать величиной сдвига t относительно первого момента, который при этом может быть задан в виде координатной переменной:
RХ(t,t+t) = M{Х(t)Х(t+t)}. (9.1.4')
Функция, задаваемая этим выражением, обычно называется автоковариационной функцией случайного процесса.
Корреляционные функции. Частным случаем ковариационной функции является функция автокорреляции (ФАК), которая широко используется при анализе сигналов:
KХ(t1,t2) = 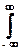
 (x(t1)-mx(t1))(x(t2)-mx(t2) p(x1,t1;x2,t2) dx1dx2. (9.1.5)
(x(t1)-mx(t1))(x(t2)-mx(t2) p(x1,t1;x2,t2) dx1dx2. (9.1.5)
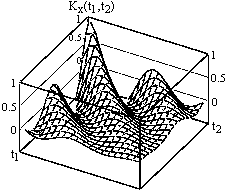 Рис. 9.1.2.
Рис. 9.1.2.
|
Для центрированных случайных процессов ФАК тождественна функции ковариации. При произвольных значениях mx корреляционные и ковариационные функции связаны соотношением:
KX(t,t+t) = RX(t,t+t) - mx2(t).
Пример функции автокорреляции приведен на рис. 9.1.2.
Нормированная функция автокорреляции (функция корреляционных коэффициентов):
rХ(t,t+t) = KХ(t,t+t) / [s(t)s(t+t)]. (9.1.6)
При t = 0 значение rХ равно 1, а ФАК вырождается в дисперсию случайного процесса:
KХ(t) = DХ(t).
Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и автокорреляции. Особой необходимости в отдельной функции дисперсии не имеется.
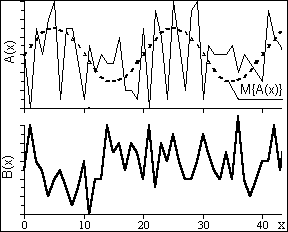 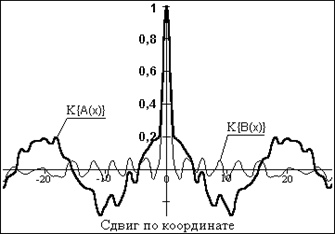 Рис. 9.1.3. Реализации случайных процессов. Рис. 9.1.4. Корреляционные функции процессов.
Рис. 9.1.3. Реализации случайных процессов. Рис. 9.1.4. Корреляционные функции процессов.
|
Примеры реализаций двух различных случайных процессов и их корреляционных функций приведены на рис. 9.1.3 и 9.1.4..
Дата добавления: 2020-02-05; просмотров: 667;











