Некоторые распределения случайных величин.
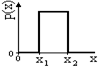 Рис. 8.3.9.
Рис. 8.3.9.
|
Равномерное распределение. Случайная величина равновероятна в интервале значений от х1 до х2 (рис. 8.3.9):
р(х) = 1/(х2-х1), х1 £ х £ х2,
= 0, х < х1, х > х2.
М{X}= (х1+х2)/2, D{X}= (x2-x1)2/12.
Для дискретной величины с N равноотстоящими друг от друга значениями:
Pi = 1/N, M{X} = (x1+x2)/2, D{X} = [(x2-x1)2/12][(N+1)/(N-1)].
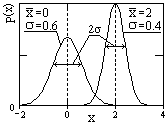 Рис. 8.3.10.
Рис. 8.3.10.
|
Распределение Гаусса (нормальное распределение). Плотность вероятностей нормального распределения случайных непрерывных величин Х задается двумя параметрами - среднего значения 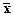 (центра распределения) и дисперсии s2:
(центра распределения) и дисперсии s2:
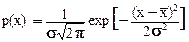 . (8.3.15)
. (8.3.15)
Пример двух распределений Гаусса при разных средних значениях и дисперсиях приведен на рис. 8.3.10.
Плотность вероятностей случайной гауссовской величины имеет только один максимум, который соответствует x = 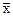 , т.е. математическому ожиданию, при этом форма распределения симметрична относительно математического ожидания. При |х| Þ ¥ ветви кривой асимптотически приближаются к нулю. Изменение математического ожидания при s = const смещает максимум распределения вдоль оси х без изменения формы кривой. Ширина плотности вероятностей распределения пропорциональна стандартному отклонению s и на уровне 0.607 от максимального значения p(x) равна 2s. Вероятность отклонений значений х от среднего значения
, т.е. математическому ожиданию, при этом форма распределения симметрична относительно математического ожидания. При |х| Þ ¥ ветви кривой асимптотически приближаются к нулю. Изменение математического ожидания при s = const смещает максимум распределения вдоль оси х без изменения формы кривой. Ширина плотности вероятностей распределения пропорциональна стандартному отклонению s и на уровне 0.607 от максимального значения p(x) равна 2s. Вероятность отклонений значений х от среднего значения 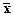 на величины, большие 3s, в нормальных распределениях равна 0.0028, что позволяет выполнять прямые и обратные прогнозные оценки:
на величины, большие 3s, в нормальных распределениях равна 0.0028, что позволяет выполнять прямые и обратные прогнозные оценки:
xmax @ 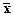 + 3s, xmin @
+ 3s, xmin @ 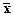 - 3s,
- 3s,
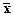 @ (xmax+xmin)/2, s @ (xmax-xmin)/6.
@ (xmax+xmin)/2, s @ (xmax-xmin)/6.
Нормальное распределение играет большую роль в теории вероятностей и в математической статистике. Основная особенность его заключается в том, что оно является предельным законом, к которому при определенных условиях приближаются другие законы распределения. В частности, независимые случайные величины Х1, Х2, ..., Хn, подчиненные каким угодно законам распределения (с весьма небольшими исключениями), при суммировании и других линейных комбинациях дают распределения, сколь угодно близкие к нормальному закону. Это позволяет нормальному распределению служить хорошей математической моделью для большинства многофакторных физических процессов. Линейные комбинации случайных гауссовских величин всегда являются гауссовскими.
Распределение Пуассона является широко распространенным распределением случайных целочисленных дискретных величин. Оно задается только одним параметром l, значение которого равно среднему значению случайных величин распределения и одновременно задает значение дисперсии распределения:
Pk = 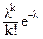 , k - целое. (8.3.16)
, k - целое. (8.3.16)
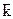 = l, Dk = l, sk =
= l, Dk = l, sk = 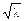 , dk = 1/
, dk = 1/ 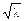 .
.
Распределение Пуассона иногда называют распределением вероятностей количества редких событий, для оценки которых оно и применяется наиболее часто, безотносительно к их физической сущности. Условия справедливости распределения Пуассона применительно к каким-либо случайным явлениям (событиям) достаточно просты:
1. Случайная величина может принимать только нулевые и целые положительные значения (как, например, число отказов аппаратуры или телефонных звонков за определенный временной интервал, число треков от альфа-частиц на площади или в объеме трекового детектора и т.п.).
2. Вероятность отдельного события на бесконечно малом пространстве счета событий, на котором ведется их регистрация (время, площадь, объем и пр.) пропорциональна величине этого пространства и при его стремлении к нулю также стремится к нулю, как бесконечно малая первого порядка, а вероятности событий более высокой кратности (2 и более событий) стремятся к нулю, как бесконечно малые более высоких порядков.
3. События в неперекрывающихся интервалах пространства счета событий статистически независимы.
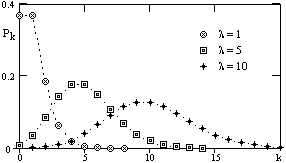 Рис. 8.3.11.
Рис. 8.3.11.
|
Пример.Средняя скорость счета фоновых гамма-квантов детектором радиометра составляет m = 1 импульс в секунду. Возможные экспозиции единичного измерения равны 1, 5 и 10 секунд. Все три условия справедливости закона Пуассона для процесса регистрации квантов выполнены. Значение l для распределения (8.3.16) будет определяться выражением l = mT, где Т - экспозиция измерения. Расчетные значения вероятностей Pk для трех различных экспозиций приведены на рис. 8.3.11. Попутно заметим, что значение l для закона Пуассона не обязано быть целочисленным.
Как видно на рис. 8.3.11, распределение Пуассона резко асимметрично при малых значениях l. По мере роста l распределение становится симметричным относительно 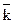 = l и при l>20 может быть аппроксимировано однопараметровым распределением Гаусса с
= l и при l>20 может быть аппроксимировано однопараметровым распределением Гаусса с 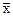 = s2 = l.
= s2 = l.
Экспоненциальное распределение. Этим законом отображается, например, распределение длительности интервалов между случайными событиями, соответствующими закону Пуассона, непосредственно из которого оно и может быть получено.
Допустим, что для рассматриваемого явления значение l распределения Пуассона определяется выражением l = nt, где n - среднее количество событий на единице интервала t (средняя скорость следования событий, если t - время). Длительность интервала между двумя последовательными событиями будет равна t+dt, если на интервале t не будет ни одного события (вероятность чего в соответствии с (8.3.16) равна Р0 = (nt)0×e-nt/0! = e-nt), а на интервале dt Þ 0 произойдет одно событие (вероятность P1 = (ndt)1×e-ndt/1! = ndt, так как e-ndt Þ 1 при dt Þ 0). События в неперекрывающихся интервалах являются статистически независимыми, а, следовательно, искомая вероятность p(t)dt интервала t будет равна произведению вероятностей Р0 и Р1, т.е. p(t)dt = e-nt×ndt, откуда получаем выражение для плотности распределения вероятностей случайной непрерывной величины t:
p(t) = n×e-nt, t ³ 0. (8.3.17)
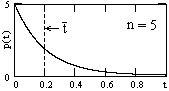 Рис. 8.3.12.
Рис. 8.3.12.
|
Пример распределения при n = 5 приведен на рис. 8.3.12. Распределение, как и положено, является нормированным:
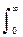 p(t) dt = 1.
p(t) dt = 1.
Среднее значение длительности интервала:
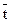 =
= 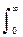 t p(t) dt = n
t p(t) dt = n 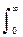 t e-nt dt = 1/n.
t e-nt dt = 1/n.
Среднее квадратическое значение:
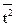 =
= 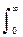 t2 p(t) dt = n
t2 p(t) dt = n 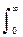 t2 e-nt dt = 2/n2.
t2 e-nt dt = 2/n2.
Дисперсия, среднее квадратическое отклонение и относительные флюктуации:
Dt = 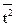 -
- 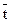 2 = 1/n2, st =
2 = 1/n2, st = 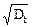 = 1/n, dt = st/
= 1/n, dt = st/ 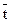 = 1.
= 1.
Как видно на рис. 8.3.12, для распределения наиболее вероятны короткие интервалы, меньшие среднего значения интервалов. Соответственно, для выдерживания среднего значения 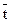 = 1/n, большее количество коротких интервалов компенсируется меньшим количеством, но длинных интервалов, в 2-3 и более раз превышающих средний интервал, что приводит к большим флюктуациям длины интервалов (среднее квадратическое отклонение равно средней длине интервалов). При работе с пуассоновскими распределениями это следует учитывать, так как длительное отсутствие регистрации событий в процессе единичной реализации какого-либо случайного процесса может вовсе не свидетельствовать об отсутствии самого процесса.
= 1/n, большее количество коротких интервалов компенсируется меньшим количеством, но длинных интервалов, в 2-3 и более раз превышающих средний интервал, что приводит к большим флюктуациям длины интервалов (среднее квадратическое отклонение равно средней длине интервалов). При работе с пуассоновскими распределениями это следует учитывать, так как длительное отсутствие регистрации событий в процессе единичной реализации какого-либо случайного процесса может вовсе не свидетельствовать об отсутствии самого процесса.
Характеристическая функция С(t) случайной величины Х с плотностью вероятностей р(х) определяется выражением:
C(v) =  p(x) exp(j2pvx) dx. (8.3.18)
p(x) exp(j2pvx) dx. (8.3.18)
Нетрудно заметить, что это выражение совпадает с обратным преобразованием Фурье функции р(х). Отсюда следует:
p(x) =  C(v) exp(-j2pvx) dv, (8.3.19)
C(v) exp(-j2pvx) dv, (8.3.19)
т.е. плотность вероятностей случайной величины может рассматриваться, как частотный спектр характеристической функции случайной величины, а последняя, в свою очередь, как координатное представление распределения случайной величины.
Через определение (или вычисление) характеристической функции упрощается нахождение моментов случайной величины любого порядка, а именно:
dnC(v)/dvn = jn  xn p(x) exp(j2pvx) dx.
xn p(x) exp(j2pvx) dx.
Принимая v = 0 и сравнивая результат с выражением (8.3.3), получаем:
mn = j-n dnC(0)/dvn = j-n C(n)(0). (8.3.20)
С помощью характеристической функции и выражений (8.3.2) можно также находить плотность вероятностей случайных величин, подвергнутых функциональным преобразованиям.
8.4. Системы случайных величины [л31,л2,л4,л15].
Свойства случайных сигналов принято описывать характеристиками совокупности случайных величин {Х1,Х2,...,Xn}, которую называют также системой или совместным распределением случайных величин. Система реализуются в процессе совместных измерений или в процессе последовательных измерений одной реализации. И в том, и в другом случае совместное распределение величин может рассматриваться как n-мерный случайный вектор Х. Теория систем случайных величин наиболее детально разработана для двух случайных величин, измеряемых по одной координате (времени, пространству и т.п.).
Пример 1.Результат накопления информации в каналах многоканального спектрометра от датчика ионизирующего излучения представляет собой совокупность (систему) случайных величин Xi (i = 1,2,...,k - номер канала спектрометра), каждая из которых распределена по закону Пуассона. Результат единичной экспозиции измерений (единичной реализации системы) - совместное распределение отсчетов xi. В совокупности эти отсчеты представляют собой k-мерный случайный вектор Х как реализацию случайного сигнала - определенного спектрального распределения излучения с математическим ожиданием отсчетов в каналах M{Xi}.
Пример 2. По стволу скважины с шагом дискретизации данных 10 см зарегистрирована цифровая диаграмма ГК - мощности экспозиционной дозы гамма-излучения пород. Последовательность цифровых отсчетов xi диаграммы (i = 1,2,...k) в силу природы радиоактивного распада представляет собой одну реализацию случайных величин Xi (k-мерный случайный вектор Х).
Пример 3. Дополнительно к мощности экспозиционной дозы в примере 2 по стволу скважины зарегистрированы цифровые диаграммы гамма-гамма-каротажа (ГГК) yi, нейтронного каротажа (НК) ni и нейтронного гамма-каротажа (НГК) zi. Эти диаграммы также могут рассматриваться как единичные реализации систем случайных величин соответственно Yi, Ni и Zi. Но одновременно однономерные совокупности случайных величин xi, yi, ni и zi (пространственные сечения) также могут рассматриваться в виде 4-х мерных систем случайных величин Xi, Yi, Ni и Zi, зарегистрированных последовательно по одной пространственной координате, равно как и в виде одной 5-ти мерной системы случайных величин X, Y, N, Z (5-ти мерный случайный вектор или 5-ти мерный случайный сигнал).
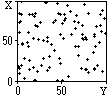 Рис. 8.4.1.
Рис. 8.4.1.
|
При рассмотрении систем случайных величин, и особенно дву- и трехмерных, удобно использовать геометрическую интерпретацию систем. Так, например, пространство системы двух случайных величин (X,Y) можно представлять себе на плоскости x0y с координатами X и Y, где каждой паре (xi,yi) реализации случайных величин соответствует точка на плоскости. На рис. 8.4.1 приведен пример такого графического отображения реализаций системы независимых случайных величин (X,Y). Аналогично в трехмерном пространстве могут отображаться трехмерные системы случайных величин.
Рассмотрение систем случайных величин будем проводить, в основном, на двумерных системах, основные положения которых легко распространяются и на многомерные системы.
Функция распределения вероятностей системы(n-мерное совместное распределение вероятностей) определяет вероятность реализации системы событий Х, как появления событий {Х1,Х2,...,Xn} в одной реализации:
P(x1,x2, ... ,xn) = P(X1 £ x1, X2 £ x2, ... ,Xn £ xn). (8.4.1)
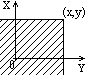 Рис. 8.4.2.
Рис. 8.4.2.
|
Геометрически (рис. 8.4.2) функция распределения системы двух случайных величин (X,Y) представляет собой вероятность реализации случайных точек в левом нижнем бесконечном квадранте (заштриховано) с вершиной в точке (x,y).
Свойства многомерной функции распределения в целом аналогичны одномерной функции и кратко могут быть описаны следующим образом:
1. 0 £ P(x1,x2, ... ,xn) £ 1, -¥ <x1< ¥, -¥ <x2< ¥ , ... , -¥ <xn< ¥.
2. P(x1,x2, ... ,xn) есть монотонно неубывающая функция по всем xi.
3. P(x1,x2, ... ,xn) = 0, если хотя бы один из аргументов равен - ¥.
4. P(x1,x2, ... ,xn) = 1, если все без исключения аргументы равны ¥.
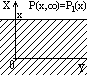 Рис. 8.4.3.
Рис. 8.4.3.
|
5. P( ¥,x2, ... ,xn) = P1(x2, ... ,xn), P(x1,¥, ... ,xn) = P2(x1,x3, ... ,xn), ... и т.д. для любых значений xi = ¥ в любых комбинациях вплоть до P(¥,¥, ... ,xn) = Pj(xn), при этом функции Pi для разных комбинаций аргументов не обязаны иметь один и тот же вид. Геометрическое отображение данного свойства для двумерной системы (X,Y) приведено на рис. 8.4.3.
Плотность вероятностей системыудовлетворяет соотношению:
p(x1,x2,...,xn) dx1 dx2 ... dxn = P{x1<X1£x1+dx1, ... ,xn<Xn£xn}. (8.4.2)
p(x1,x2,...,xn) = 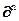 P(x1,x2, ... ,xn) /
P(x1,x2, ... ,xn) / 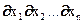 . (8.4.3)
. (8.4.3)
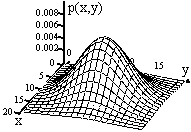 Рис. 8.4.4.
Рис. 8.4.4.
|
Плотность вероятностей двумерной системы можно изобразить геометрически в виде поверхности распределения вероятностей, пример которой приведен на рис. 8.4.4.
Свойства многомерной плотности распределения вероятностей вытекают из свойств функции распределения вероятностей и в целом аналогичны одномерной плотности вероятностей, а именно (на примере двумерной плотности вероятностей):
1. p(x,у) ³ 0, - ¥ < x < ¥, - ¥ < x < ¥. Плотность вероятностей не отрицательна.
2. 
 p(x,у) dx dy = 1. Сумма вероятностей всех возможных значений системы случайных величин (X,Y) по пространству состояний равна 1.
p(x,у) dx dy = 1. Сумма вероятностей всех возможных значений системы случайных величин (X,Y) по пространству состояний равна 1.
3. 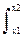
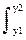 p(x,y) dx dy = P(x1<X£x2, y1<Y£y2). Двойной интеграл от плотности вероятностей по определенным интервалам случайных величин Х и Y равен вероятности реализации системы случайных величин в этом интервале значений Х и Y.
p(x,y) dx dy = P(x1<X£x2, y1<Y£y2). Двойной интеграл от плотности вероятностей по определенным интервалам случайных величин Х и Y равен вероятности реализации системы случайных величин в этом интервале значений Х и Y.
По известной n-мерной плотности вероятностей может определяться m-мерная плотность при m<n интегрированием по "лишним" координатам:
p(x1,x2,...,xm) =  ...
...  p(x1,x2,...,xn) dxm+1 ... dxn. (8.4.4)
p(x1,x2,...,xn) dxm+1 ... dxn. (8.4.4)
Условные законы распределения. Выражение (8.4.4) при известном законе плотности распределения вероятностей системы случайных величин позволяет определить плотность вероятностей любой из случайных величин, входящих в систему. Обратная задача не может решаться столь просто, поскольку известные законы распределения отдельных случайных величин не определяют связей между величинами, если последние существуют. Для решения задачи требуется задание условных законов распределения, т.е. плотности распределения вероятностей одной случайной величины при определенных значениях других случайных величин.
Случайные величины, входящие в систему, реализуются совместно. С учетом этого, условные законы распределения случайных величин можно получить переходом от условных вероятностей совместных событий (8.2.10-12) к плотности распределения вероятностей. В общем случае, условные законы распределения также могут быть многомерными, т.е. определять вероятность реализации одной из случайных величин при условии реализации определенных значений других величин системы. Однако на практике даже для многомерных систем используются, в основном, попарные двумерные зависимости. Так, для двумерных случайных систем условные плотности вероятностей величины X по значениям величины Y и величины Y по Х определяются выражениями:
p(x/y) = p(x,y)/p(y), p(y/x) = p(x,y)/p(x). (8.4.5)
Отсюда, определение плотности вероятностей двумерной системы производится по формулам:
p(x,y) = p(x)×p(y/x) º p(y)×p(x/y). (8.4.6)
При известных многомерных законах распределений анализ попарных двумерных распределений производится с использованием выражения (8.4.4).
Функции регрессии.Из выражений (8.4.5-6) следует, что в системе зависимых случайных величин математические ожидания величин также являются зависимыми, т.е. функциями средних значений одной величины от значений другой величины:
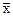 (y) = M{X/y}=
(y) = M{X/y}=  x p(x/y) dx,
x p(x/y) dx, 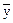 (x) = M{Y/x}=
(x) = M{Y/x}=  y p(y/x) dy. (8.4.7)
y p(y/x) dy. (8.4.7)
Уравнения
x = 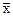 (y), y=
(y), y= 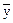 (x) (8.4.8)
(x) (8.4.8)
называются уравнениями регрессии соответственно X по Y и Y по Х. В общем случае уравнения регрессии для многомерных систем также могут быть многомерными, типа x = 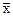 (y,z,...) и пр.
(y,z,...) и пр.
Статистическая независимость случайных величин.Для совместной системы случайных величин X случайные величины системы (X1, X2, ...) статистически независимы друг от друга, если реализация одной из величин ни каким образом не определяет и не влияет на реализацию других величин. Так, например, при игре в кости реализация в одном бросании числа на одном кубике не влияет на появление каких-либо чисел на других кубиках. Если такая зависимость появляется, то это свидетельствует о мошенничестве.
Статистически независимы, как правило, случайные величины, связанные с источниками различной физической природы. В строго корректном понимании данного термина случайные события статистически независимы тогда и только тогда, когда выполняется условие:
p(x1,x2,...,xn) = p1(x1) p2(x2) ... pn(xn). (8.4.9)
Пример.Определить независимость случайных величин Х и Y в двумерной системе по заданной плотности распределения вероятностей системы.
1. p(x,y) = 1/[p2(1+x2+y2+x2y2)]. Выражение 1+x2+y2+x2y2 может быть разделено по переменным на множители (1+х2)(1+у2), а, следовательно, p(x,y) = p(x)×p(y). Случайные величины Х и Y независимы.
2.p(x,y) = x+y, 0 £ x £ 1, 0 £ y £ 1. Cоответствующие одномерные плотности вероятностей:
p(x) = 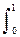 (x+y) dy = x+1/2, p(y) =
(x+y) dy = x+1/2, p(y) = 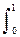 (x+y) dx = y+1/2. p(x,y) ¹ p(x)×p(y). Величины Х и Y зависимы.
(x+y) dx = y+1/2. p(x,y) ¹ p(x)×p(y). Величины Х и Y зависимы.
Условные плотности вероятностей по (8.4.5): p(x/y) = (x+y)/(y+0.5), p(y/x) = (x+y)/(x+0.5).
Моменты систем случайных величин.Вычисление моментов случайных величин с использованием многомерной плотности вероятностей может производиться как по отдельным величинам Xi, так и на любые их комбинации (смешанные моменты). Так, вычисление средних значений и дисперсий любых случайных величин, входящих в n-мерную систему, производится по формулам:
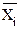 =
=  ...
...  xi p(x1,x2,...,xn) dx1dx2...dxn, (8.4.10)
xi p(x1,x2,...,xn) dx1dx2...dxn, (8.4.10)
sxi2 =  ...
...  (xi-
(xi- 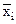 )2 p(x1,x2,...,xi) dx1dx2...dxn. (8.4.11)
)2 p(x1,x2,...,xi) dx1dx2...dxn. (8.4.11)
Для случайных дискретных величин интегрирование соответственно заменяется суммированием, а плотности распределения вероятностей на распределения вероятностей.
Ковариация и корреляция. Смешанные начальные моменты второго порядка носят название ковариационных моментов системы случайных величин. Для двумерных систем:
R12 = M{X1X2}= 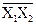 =
= 
 x1x2 p(x1,x2) dx1dx2. (8.4.12)
x1x2 p(x1,x2) dx1dx2. (8.4.12)
В общем случае, для n-мерной системы случайных величин:
Rij = M{XiXj}= 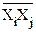 =
=  ...
...  xixj p(x1,x2,...,xn) dx1dx2...dxn, i,j = 1...n (8.4.13)
xixj p(x1,x2,...,xn) dx1dx2...dxn, i,j = 1...n (8.4.13)
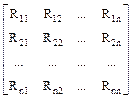 Матрица Rij
Матрица Rij
|
Значения моментов Rij образуют матрицу размером n ´ n попарной ковариации всех случайных величин, входящих в систему. С учетом того, что имеет место равенство Rij = Rji, ковариационная матрица (см. пример) симметрична относительно главной диагонали i = j, при этом ковариационные моменты на главной диагонали матрицы представляют собой средние значения квадратов случайных величин Xi, т.к. 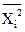 = Rij при i = j.
= Rij при i = j.
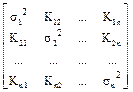 Матрица Kij
Матрица Kij
|
Смешанные центральные моменты второго порядка называют корреляционными моментами системы случайных величин. Они, как и ковариационные моменты, также образуют матрицу моментов системы, симметричную относительно главной диагонали, при этом значения моментов на главной диагонали представляют собой значения дисперсий si2 = Kij при i = j соответствующих случайных величин Xi (см. пример).
Kij = M{(Xi- 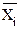 )(Xj-
)(Xj- 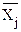 )}=
)}=  ...
...  (xi-
(xi- 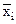 )(xj-
)(xj- 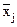 ) p(x1,x2,...xn) dx1dx2...dxn (8.4.14)
) p(x1,x2,...xn) dx1dx2...dxn (8.4.14)
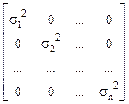 Матрица si2
Матрица si2
|
Корреляционные моменты является количественной мерой степени статистической связи (взаимной зависимости или корреляции) случайных величин Хi и Хj. Для системы случайных некоррелированных величин матрица корреляционных моментов является диагональной матрицей дисперсий с нулевыми значениями Kij при i ¹ j (см. пример матрицы si2).
Из выражений (8.4.13) и (8.4.14) следует достаточно простая связь между ковариационными и корреляционными моментами:
Kij = Rij - 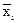 ×
× 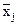 .
.
В качестве безразмерной нормированной характеристики степени корреляции случайных величин используют также понятие коэффициентов корреляции, которые также образуют симметричную относительно главной диагонали матрицу со значениями, равными 1, по главной диагонали:
rij = Kij /(sisj) = ( 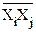 -
- 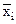
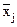 )/sisj. (8.4.15)
)/sisj. (8.4.15)
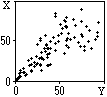 Рис. 8.4.5.
Рис. 8.4.5.
|
Значения коэффициентов корреляции заключены в пределах от -1 до +1. При r = 0 случайные величины считаются независимыми друг от друга (например, величины (Х,Y) на рис. 8.4.1), при |r| = 1 - полностью коррелированными (например, величины Х = b×Y с произвольным значением коэффициента b), во всех остальных случаях чем ближе значение |r| к 1, тем больше корреляция между случайными величинами, которая может иметь как прямой, так и обратный характер (при r<0). Величины Х и Y на рис. 8.4.5 явно коррелированны между собой с определенным коэффициентом прямой корреляции.
Попутно заметим, что если коэффициенты корреляции статистически независимых случайных величин всегда равны нулю, то обратное утверждение о статистической независимости случайных величин, если равен нулю их коэффициент корреляции, справедливо только для гауссовских распределений, а в общем случае является недостаточным. Полную гарантию статистической независимости дает только выполнение условия (8.4.9).
С учетом выражения (8.4.9) смешанные моменты статистически независимых случайных величин разделяются на произведения интегральных сомножителей. В частности, для ковариационных моментов случайных двумерных величин имеем:
M{X1X2} =  x1 p1(x1) dx1
x1 p1(x1) dx1  x2 p2(x2) dx2 = M{X1}M{X2}, (8.4.16)
x2 p2(x2) dx2 = M{X1}M{X2}, (8.4.16)
т.е. математическое ожидание произведения двух статистически независимых случайных величин равно произведению их математических ожиданий. Если математическое ожидание хотя бы одной из случайных величин будет равно нулю, то нулю становится равным и их произведение.
Пример.Плотность вероятностей задана выражением: p(x,y) = x+y, 0 £ x £ 1, 0 £ y £ 1.
Одномерные плотности вероятностей: p(x)= 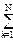 (x+y) dy =x+1/2, p(y)=
(x+y) dy =x+1/2, p(y)= 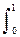 (x+y) dx = y+1/2.
(x+y) dx = y+1/2.
Математические ожидания и дисперсии:
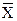 =
= 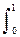 x(x+1/2) dx = 7/12, Dx =
x(x+1/2) dx = 7/12, Dx = 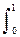 (x-7/12)2 (x+1/2) dx = 11/144.
(x-7/12)2 (x+1/2) dx = 11/144.
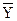 =
= 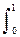 y(y+1/2) dy = 7/12, Dy =
y(y+1/2) dy = 7/12, Dy = 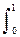 (y-7/12)2 (y+1/2) dy = 11/144.
(y-7/12)2 (y+1/2) dy = 11/144.
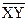 =
= 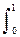
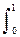 xy(x+y) dx dy = 1/3.
xy(x+y) dx dy = 1/3.
Коэффициент корреляции: rxy = ( 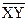 -
- 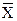
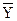 )/sxsy = (1/3 - (7/12)2)/(11/144) = -1/11.
)/sxsy = (1/3 - (7/12)2)/(11/144) = -1/11.
Замечание по терминологии. В современной технической литературе существует достаточно большая путаница по применению терминов ковариации и корреляции. Очень часто термин корреляции применяют как к центрированным, так и нецентрированным системам случайных величин и случайных процессов. В какой-то мере это можно считать допустимым, так как и то, и другое понятие применяется для характеристики корреляционной связи (взаимной зависимости) случайных величин. С другой стороны, матрицу смешанных центральных моментов второго порядка так же часто называют матрицей ковариации, и т.п.
Во избежание дальнейшей путаницы в понятиях примем за основу следующее. Однозначно понимаемым и повсеместно принятым термином теории вероятностей и математической статистики является коэффициент корреляции, который вычисляется по формуле (8.4.15) с использованием центральных моментов. А потому представляется логичным именно матрицу смешанных центральных моментов и смешанные моменты второго порядка центрированных случайных величин называть корреляционными, а смешанные начальные моменты нецентрированных случайных величин - ковариационными. Такой подход применен, например, в работе /л4/ и показал себя весьма эффективным в строгой логике математических построений.
Сумма и разность случайных величинанализируются достаточно просто с предварительным вычислением одномерных плотностей вероятностей соответствующих величин по формуле (8.4.4) или с использованием непосредственно плотностей вероятностей суммируемых случайных величин, если известны только последние и неизвестна многомерная плотность вероятностей, что чаще всего и имеет место на практике.
Средние значения сумм (разностей) случайных величин вычисляются по формулам:
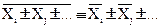 , (8.4.17)
, (8.4.17)
так как математические ожидания сумм и разностей случайных величин равны соответствующим суммам и разностям их математических ожиданий. Средние значения случайных величин вычисляются по одномерным плотностям вероятностей.
Дисперсия суммы (разности) случайных величин может быть получена с использованием выражений, следующих из (8.3.9') и (8.4.15):
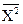 = sx2 +
= sx2 + 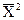 ,
, 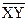 =
= 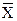
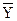 + rxy sx sy
+ rxy sx sy
Применяя эти выражения при вычислении среднего значения квадрата суммы (разности) двух случайных величин, получаем:
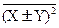 =
= 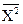 ± 2
± 2 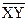 +
+ 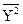 = sx2 +
= sx2 + 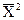 ± 2
± 2 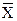
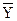 ± 2 rxy sx sy + sy2 +
± 2 rxy sx sy + sy2 + 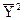 =
=
sx2 + sy2 ± 2 rxy sx sy + ( 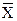 ±
± 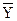 )2.
)2.
Отсюда, перенося последний член выражения в левую часть:
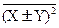 - (
- ( 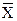 ±
± 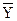 )2 º (sx±y)2 = sx2 + sy2 ± 2 rxy sx sy. (8.4.18)
)2 º (sx±y)2 = sx2 + sy2 ± 2 rxy sx sy. (8.4.18)
Если случайные величины не коррелированны, то дисперсия их суммы или разности равна сумме их дисперсий.
Плотность вероятностей суммы (разности) случайных величин по известным плотностям вероятностей суммируемых величин в общем случае определяется достаточно сложно. Задача значительно облегчается, если случайные величины статистически независимы. Рассмотрим этот случай на примере случайной двумерной величины Z=X+Y с известными плотностями вероятностей px(x) и py(y).
Совместная плотность вероятностей p(z) = p(x,y) определяет функцию распределения вероятностей P(z) = P(Z £ z) = P(X+Y £ z), причем для каждой совместной реализации имеем z=x+y и, соответственно, x=z-y и y=z-x. Отсюда, с учетом статистической независимости случайных величин X и Y, и, соответственно, p(x,y) = px(x)×py(y), для распределения вероятностей P(z) имеем:
P(z) = 
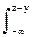 p(x,y) dx dy =
p(x,y) dx dy =  py(y)
py(y) 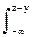 px(x) dx dy. (8.4.19)
px(x) dx dy. (8.4.19)
Продифференцируем данное выражение по z и, поскольку переменная z присутствует только в верхнем пределе второго интеграла, получим:
d P(z)/dz º p(x,y) =  py(y) px(z-y) dy º py(y) * px(z-y). (8.4.20)
py(y) px(z-y) dy º py(y) * px(z-y). (8.4.20)
Аналогично, если принять y=z-x в качестве верхнего предела во втором интеграле выражения (8.3.19), можно получить:
p(x,y) =  px(x) py(z-x) dx º px(x) * py(z-x). (8.4.20')
px(x) py(z-x) dx º px(x) * py(z-x). (8.4.20')
Таким образом, двумерная плотность вероятностей суммы случайных величин равна свертке их одномерных плотностей распределения вероятностей.
Для разности случайных величин Z=X-Y в выражении (8.3.19) верхний предел заменяется соответственно на z+y, при этом:
p(x,y) =  py(y) px(z+y) dy º
py(y) px(z+y) dy º  py(x-z) px(x) dx. (8.4.21)
py(x-z) px(x) dx. (8.4.21)
Сумма и разность нормальных распределений. Плотность вероятностей суммы Z=X+Y двух нормальных распределений случайных величин X и Y получается непосредственной подстановкой выражений гауссовских распределений (8.3.15) в (8.4.20):
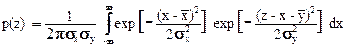
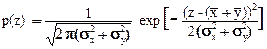 . (8.4.22)
. (8.4.22)
Аналогично для разности двух случайных величин Z=X-Y:
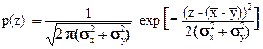 . (8.4.23)
. (8.4.23)
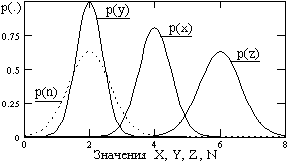 Рис. 8.4.6.
Рис. 8.4.6.
|
Как видно из полученных выражений, сумма и разность двух независимых нормально распределенных случайных величин также распределена нормально с дисперсией, равной сумме дисперсий исходных случайных величин, и со средними значениями, соответственно равными сумме и разности средних значений исходных величин. На рис. 8.4.6 в качестве примера приведены графики нормальных распределений случайных величин X ( 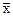 =4, sx=0.5), Y (
=4, sx=0.5), Y ( 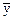 =2, sy=0.4) и Z=X+Y, N=X-Y.
=2, sy=0.4) и Z=X+Y, N=X-Y.
Эти выводы действительны для сумм и разностей произвольного количества нормально распределенных случайных величин в любых сочетаниях и результатом всегда будет случайная величина с нормальной плотностью распределения вероятностей. Это свойство называется устойчивостью закона распределения случайной величины, и оно является достаточно редким. Для гауссовских распределений это свойство сохраняется даже для коррелированных случайных величин, естественно с определением дисперсии по выражению (8.4.18). А так как функция распределения Гаусса относится к числу собственных, то функции дифференцирования, интегрирования и других линейных преобразований гауссовского распределения также являются нормальными.
Дата добавления: 2020-02-05; просмотров: 1062;











