Свойства функций автокорреляции и автоковариации.

1. Максимум функций наблюдается при t = 0. Это очевидно, т.к. при t = 0 вычисляется степень связи отсчетов с собой же, которая не может быть меньше связи разных отсчетов. Значение максимума функции ковариации равно средней мощности сигнала.

2. Функции ковариации и автокорреляции являются четными: R_X(t) = R_X(-t). Последнее также очевидно: X(t)X(t+t) = X(t-t)X(t) при t = t-t. Говоря иначе, смешанные моменты двух случайных величин X(t₁) и X(t₂) не зависят от последовательности, в которой эти величины рассматриваются, и соответственно симметричны относительно своих аргументов: R_x(t₁,t₂) = R_x(t₂,t₁), равно как и K_x(t₁,t₂) = K_x(t₂,t₁), что наглядно видно на рис. 9.1.2.

3. При t Þ ¥ значения ФАК для сигналов, конечных по энергии, стремятся к нулю, что прямо следует из физического смысла ФАК. Это позволяет ограничивать длину ФАК определенным максимальным значением t_max - радиусом корреляции, за пределами которого отсчеты можно считать независимыми. Интегральной характеристикой времени корреляции случайных величин обычно считают эффективный интервал корреляции, определяемый по формуле:

T_k =2 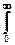|r_x(t)| dt º (2/K_x(0) 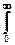|K_x(t)| dt. (9.1.7)

Отсчеты (сечения) случайных функций, отстоящие друг от друга на расстояние большее T_k, при инженерных расчетах считают некоррелированными.

Заметим, что для некоррелированных процессов при t Þ ¥ значение T_k стремится к 2, что несколько противоречит физическому смыслу радиуса корреляции, который в этом случае должен был бы стремиться к 1. С учетом последнего эффективный интервал корреляции целесообразно определять по формуле:

T_k =2 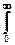|r_x(t)| dt - 1 º (2/K_x(0) 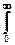|K_x(t)| dt - 1. (9.1.7')

4. Если к случайной функции X(t) прибавить неслучайную функцию f(t), то корреляционная функция не изменяется.

Обозначим новую случайную функцию как Y(t)=X(t)+f(t). Функция математического ожидания новой величины: 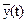= 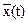+ f(t). Отсюда следует, что Y(t) - 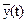= X(t) - 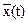, и соответственно K_y(t₁,t₂) = K_x(t₁,t₂).

5. Если случайную функцию X(t) умножить на неслучайную функцию f(t), то ее корреляционная функция R_x(t₁,t₂) умножится на f(t₁)×f(t₂). Обоснование данного свойства проводится по методике, аналогичной предыдущему пункту.

6. При умножении функции случайного процесса на постоянное значение С значения ФАК увеличиваются в С² раз.

Взаимные моменты случайных процессов второго порядка дают возможность оценить совместные свойства двух случайных процессов X(t) и Y(t) путем анализа произвольной пары выборочных функций x_k(t) и y_k(t).

Мера связи между двумя случайными процессами X(t) и Y(t) также устанавливается корреляционными функциями, а именно - функциями взаимной ковариации и взаимной корреляции, в общем случае для произвольных фиксированных моментов времени t₁ = t и t₂ = t+t:

R_XY(t,t+t) = M{(X(t)(Y(t+t)}. (9.1.8)

K_XY(t,t+t) = M{(X(t)-m_x(t))(Y(t+t)-m_y(t+t))}. (9.1.9)

Взаимные функции являются произвольными функциями (не обладают свойствами четности или нечетности), и удовлетворяют следующим соотношениям:

R_xy(-t) = R_yx(t), (9.1.10)

|R_xy(t)|² £ R_x(0)R_y(0).

Если один из процессов центрированный, то имеет место R_xy(t) = K_xy(t).

Нормированная взаимная корреляционная функция (коэффициент корреляции двух процессов), которая характеризует степень линейной зависимости между случайными процессами при данном сдвиге t одного процесса по отношению ко второму, определяется выражением:

r_xy(t) = K_xy(t)/(s_xs_y). (9.1.11)

Классификация случайных процессов. Случайные процессы различают по степени однородности их протекания во времени (по аргументу).

Нестационарные процессы. В общем случае значения функций математического ожидания, дисперсии и ковариации могут быть зависимыми от момента времени t, т.е. изменяться во времени. Такие процессы составляют класс нестационарных процессов.

Стационарные процессы. Процесс называют стационарным, если плотность вероятностей процесса не зависит от начала отсчета времени и если на интервале его существования выполняются условия постоянства математического ожидания и дисперсии, а ковариационная функция является функцией только разности аргументов t = t₂-t₁, т.e.:

m_Х(t₁) = m_Х(t₂) = m_Х = const, (9.1.12)

D_Х(t₁) = D_Х(t₂) = D_Х = const,

R_Х(t₁,t₁+t) º R_x(t₂-t,t₂) = R_Х(t) º R_Х(-t).

Последнее выражение свидетельствует о четности ковариационной (а равно и корреляционной) функции. Из него вытекает также еще одно свойство смешанных моментов стационарных процессов:

|R_x(t)| £ R_x(0), |K_x(t)| £ K_x(0) º D_x.

Среди стационарных процессов выделяют строго стационарные процессы, для которых постоянны во времени не только математическое ожидание, дисперсия и ковариация, но и все остальные моменты высших порядков (в частности, асимметрия и эксцесс).

Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. Теория стационарных случайных функций разработана наиболее полно и для ее использования обычно достаточно определения стационарности в широком смысле: случайная функция считается стационарной, если ее математическое ожидание постоянно, а ковариационная функция зависит только от одного аргумента. Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.

Эргодические процессы. Строго корректно характеристики случайных процессов оцениваются путем усреднения по ансамблю реализаций в определенные моменты времени (по сечениям процессов). Но большинство стационарных случайных процессов обладает эргодическим свойством, сущность которого заключается в том, что по одной достаточно длинной реализации процесса можно судить о всех его статистических свойствах так же как по любому количеству реализаций. Другими словами, закон распределения случайных величин в таком процессе может быть одним и тем же как по сечению для ансамбля реализаций, так и по координате развития. Такие процессы получили название эргодических.

Практическая проверка эргодичности процесса обычно производится проверкой выполнения условия Слуцкого:

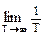
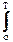K(t) dt = 0. (9.1.13)

Эргодичность является очень важным свойством случайных стационарных, и только стационарных процессов. Для эргодических процессов определение статистических характеристик усреднением по ансамблю реализаций может заменяться усреднением по множеству неперекрывающихся интервалов только одной реализации:

M{Х(t)} » m_Х,N(t) = (1/N) 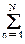Х(t_n), (9.1.14)

D_Х(t) = M{Х(t) - m_Х,N(t)]²} » s_Х²(t) = (1/N) 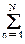( Х_n(t) - m_Х,N(t_n))², (9.1.15)

R_Х(t) = M{Х(t)Х(t+t)} » R_Х,N(t) = (1/N) 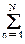Х(t_n)Х(t_n+t), (9.1.16)

где N- интервал усреднения и корреляции для числовых рядов. Так как определение функций производится по ограниченным статистическим данным одной реализации и является только определенным приближением к соответствующим фактическим функциям процессов, целесообразно называть эти функции статистическими. Заметим, что как это следует из (9.1.16), вычисление ковариационной функции подобно свертке (с делением на интервал корреляции) и может записываться символически:

R_Х,N(t) = (1/N) Х(t) _* Х(t+t).

Свойства эргодичности могут проявляться только по отношению к двум первым моментам случайного процесса, что вполне достаточно для использования соответствующих методик исследования процессов. На практике оценку эргодичности обычно производят по корреляционной функции. Если корреляционная функция процесса стремится к нулю при возрастании значения аргумента (t), то процесс относится к числу эргодических, по крайней мере относительно моментов первого и второго порядков.

Пример.Случайная функция задана выражением Z(t) = X(t)+Y, где X(t) - стационарная эргодичная функция, Y - случайная величина, некоррелированная с X(t). Эргодична ли функция Z(t) ?

m_z(t) = m_z(x)+m_y, K_z(t) = K_x(t)+D_y.

Функция Z(t) стационарна, но не эргодична, так как при t Þ ¥ имеет место K_z(t) Þ D_y.

9.2. Функции спектральной плотности [л31,л4,л32].

Каноническое разложение случайных функций. Введем понятие простейшей случайной функции, которая определяется выражением:

X(t) = X×j(t), (9.2.1)

где Х - обычная случайная величина, j(t) - произвольная неслучайная функция. Математическое ожидание простейшей случайной функции:

m_x(t) = M{Xj(t)}= j(t)×M{X}= j(t)×m_x, (9.2.2)

где m_x - математическое ожидание случайной величины Х. При m_x = 0 математическое ожидание m_x(t) также равно нулю для всех t и функция (9.2.1) в этом случае называется элементарной случайной функцией. Корреляционная функция элементарной случайной функции определится выражением:

K_x(t₁,t₂) = M{X(t₁)X(t₂)}= j(t₁)j(t₂)×M{X²}= j(t₁)j(t₂)×D_x. (9.2.3)

где D_x - дисперсия случайной величины Х.

Центрированную случайную функцию ⁰X(t) можно представить суммой взаимно некоррелированных элементарных случайных функций:

⁰X(t) = 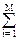X_i×j_i(t), (9.2.4)

Из взаимной некоррелированности элементарных случайных функций следует взаимная некоррелированность величин X_i. Математическое ожидание и корреляционная функция случайной функции ⁰X(t):

M{⁰X(t)}= M{ 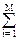X_i×j_i(t)}= 0.

K_x(t₁,t₂) = M{⁰X(t₁) ⁰X(t₂)}= M{ 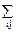X_i×j_i(t₁)X_j×j_j(t₂)}= 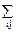j_i(t₁)j_j(t₂)M{X_iX_j}.

В силу взаимной некоррелированности парных значений X_iX_j имеет место M{X_iX_j}= 0 при i ¹ j, и все члены суммы в последнем выражении равны нулю, за исключением значений при i = j, для которых M{X_iX_j}= M{X_i²}= D_i. Отсюда:

K_x(t₁,t₂) = 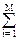j_i(t₁)j_i(t₂)D_i. (9.2.5)

Произвольная нецентрированная случайная функция соответственно может быть представлена в виде

X(t) = m_x(t) + ⁰X(t) = m_x(t) + 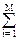X_i×j_i(t), (9.2.6)

с математическим ожиданием m_x(t) и с той же самой корреляционной функцией (9.2.5) в силу свойств корреляционных функций, где ⁰X(t) - флюктуационная составляющая случайной функции X(t). Выражение (9.2.6) и является каноническим разложением функции X(t). Случайные величины X_i называются коэффициентами разложения, функции j_i - координатными функциями разложения. При t₁ = t₂ из (9.2.5) получаем функцию дисперсии случайной функции X(t):

D_x(t) = 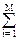[j_i(t)]²×D_i. (9.2.7)

Таким образом, зная каноническое разложение (9.2.6) функции X(t), можно сразу определить каноническое разложение (9.2.5) ее корреляционной функции, и наоборот. Канонические разложения удобны для выполнения различных операций над случайными функциями. Это объясняется тем, что в разложении зависимость функции от аргумента t выражается через неслучайные функции j_i(t), а соответственно операции над функцией X(t) сводятся к соответствующим операциям математического анализа над координатными функциями j_i(t).

В качестве координатных функций разложения, как и при анализе детерминированных сигналов, обычно используются гармонические синус-косинусные функции, а в общем случае комплексные экспоненциальные функции exp(jwt). С учетом последнего предварительно рассмотрим особенности представления случайных функций в комплексной форме.

Комплексные случайные функции. В общем случае случайный процесс может описываться комплексной случайной функцией:

Z(t) = X(t) + jY(t), (9.2.8)

где X(t) и Y(t) - действительные случайные функции. Соответственно, математическое ожидание комплексной функции:

m_z(t) = m_x(t)+j×m_y(t). (9.2.9)

Заметим, что комплексное представление случайных функций не более чем удобная для анализа математическая форма их отображения, которая, с использованием выражений Эйлера, всегда может быть переведена в форму вещественных функций. Функции дисперсии, ковариации и корреляции должны представлять собой однозначные и неслучайные вещественные характеристики случайных процессов и функций, независимо от формы их математического представления. Это условие будет выполняться при использовании в выражениях моментов второго порядка операций умножения комплексных функций с комплексно сопряженными функциями. Так, выражение для вычисления ковариационной функции имеет следующий вид:

R_z(t₁,t₂) = M{Z(t₁)× 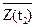}= M{[X(t₁)+jY(t₁)][(X(t₂)-jY(t₂)]}=

= M{X(t₁)X(t₂)+Y(t₁)Y(t₂)+j×[Y(t₁)X(t₂)-X(t₁)Y(t₂)]} =

= R_x(t₁,t₂) + R_y(t₁,t₂) + j×[R_yx(t₁,t₂) - R_xy(t₁,t₂)]. (9.2.10)

Если действительные и мнимые части комплексной функции некоррелированы, то R_yx = R_xy = 0 и последний член выражения (9.2.10) также равен нулю.

Аналогичное выражение имеет место и для корреляционной функции. При t₁ = t₂ = t для функции дисперсии комплексной случайной величины имеем:

D_z(t) = M{|Z(t)-m_z(t)|²} = D_x(t) + D_y(t), (9.2.11)

Все приведенные выражения в общем случае могут использоваться для любых комплексных случайных функций с любым физическим смыслом переменной t.

Финитное преобразование Фурьеслучайных функций. По аналогии с функциями детерминированных сигналов, отдельно взятая на интервале 0-Т реализация x_k(t) стационарного случайного процесса ⁰X(t) может быть представлена в виде ряда Фурье:

x_k(t) = 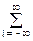V_x,k(w_i) exp(jw_it), (9.2.12)

V_x,k(w_i) = (1/T) 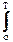x_k(t) exp(-jw_it) dt, (9.2.13)

или, в односторонней тригонометрической форме:

x_k(t) = A_x,k(0)/2 + 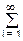(A_x,k(w_i) cos(w_it) + B_x,k(w_i) sin(w_it)), (9.2.12')

A_x,k(w_i) = (2/T) 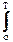x_k(t) cos(w_it) dt, (9.2.13')

B_x,k(w_i) = (2/T) 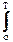x_k(t) sin(w_it) dt. (9.2.13'')

где w_i = i×Dw - частоты спектра, Dw = 2p/T - шаг по частоте. Выражения (9.2.13) обычно называют спектральными характеристиками реализаций. Из сравнения выражений (9.2.4) и (9.2.12) нетрудно сделать заключение, что выражения (9.2.12) относится к числу канонических разложений случайных функций, при этом спектральная характеристика V_x,k(w) = (A_x,k(w) - jB_x,k(w))/2, а равно и ее составляющие A_x,k(w) и B_x,k(w), также являются случайными функциями частоты - единичными реализациями случайных функций V_x(w), A_x(w) и B_x(w). Соответственно, и частотное распределение амплитуд и фаз составляющих гармонических колебаний случайного процесса ⁰X(t) представляет собой случайные функции с соответствующими неслучайными функциями дисперсий.

Если функция ⁰X(t) является дискретной последовательностью случайных величин ⁰X(n×Dt) в интервале по n от 0 до N, то, как это и положено для дискретных преобразований Фурье, расчет спектральных характеристик выполняется в Главном частотном диапазоне (до частоты Найквиста w_N = p/Dt), с заменой в выражениях (9.2.13) интегрирования на суммирование по n и с соответствующим изменением пределов суммирования в выражениях (9.2.12). Данное пояснение сохраняется и на все дальнейшие выкладки.

Спектральные характеристики единичных реализаций случайных процессов интереса, как правило, не представляют и на практике используются довольно редко. Спектральная характеристика случайной функции ⁰X(t), как ансамбля реализаций, может быть определена осреднением функций (9.2.12-13) по реализациям, в результате которого мы получим те же самые функции (9.2.12-13), только без индексов k. При этом, в силу центрированности стационарной случайной функции ⁰X(t), мы должны иметь:

M{X(t)} = 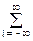M{V_x(w_i)} exp(jw_it) = 0, (9.2.14)

Последнее будет выполняться при условии M{V_x(w_i)} = 0, т.е. математическое ожидание значений спектральной характеристики центрированного стационарного случайного процесса должно быть равно нулю на всех частотах. Другими словами, спектральной характеристики центрированного стационарного случайного процесса не существует. Существуют только спектральные характеристики его отдельных реализаций, которые и используются, например, для моделирования этих реализаций.

Для произвольных нецентрированных случайных процессов X(t), при записи последних в форме X(t) = m_x(t) + ⁰X(t), будем соответственно иметь преобразование Фурье:

m_x(t) + ⁰X(t) ó m_x(w) + V_x(w) = m_x(w),

т.е., по существу, функцию спектра (или спектральной плотности) неслучайной функции математического ожидания случайного процесса, естественно, в пределах той точности, которую может обеспечить выборочный ансамбль реализаций.

С учетом вышеизложенного, под спектрами случайных процессов (или спектральной плотностью при интегральном преобразовании Фурье) повсеместно понимается не преобразования Фурье собственно случайных функций, а преобразования Фурье корреляционных функции случайных процессов.

Спектр функций случайных процессов.При представлении корреляционной функции на интервале 0-Т, шаг по спектру функции устанавливается с учетом четности корреляционной функции Dw = p/T, w_i = i×Dw, а спектр определяется обычно непосредственно по косинусам в односторонней форме:

K_x(t) = D_x(0)/2 + 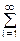D_x(w_i) cos(w_it), (9.2.15')

D_x(w_i) = (2/T) 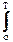K_x(t) cos(w_it) dt, (9.2.16')

где D_x(w_i) в соответствии с (9.2.5) - дисперсии случайных величин V_x(w_i), а равно и A_x(w_i) и B_x(w_i), в разложениях (9.2.12). В комплексной форме, как обычно:

K_x(t) = 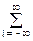D_x(w_i) exp(jw_it), (9.2.15)

D_x(w_i) = (1/T) 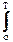K_x(t) exp(-jw_it) dt, (9.2.16)

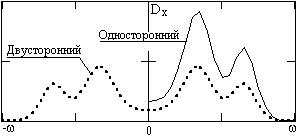Рис. 9.2.1. Спектры случайных функций.

Спектры случайных функций всегда ограничены (D(w) ¹ ¥) и неотрицательны (D(w) ³ 0), при двустороннем представлении всегда четные (D(-w) = D(w)). Пример спектров в одно- и двустороннем представлении приведен на рис. 9.2.1.

Дисперсия стационарного случайного процесса X(t) может определяться по формуле (9.2.15) при t = 0:

D_x = 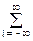D_x(w_i), (9.2.17)

т.е. дисперсия стационарного случайного процесса равна сумме дисперсий всех случайных гармоник ее спектрального разложения.

Обобщенной характеристикой спектра случайного процесса служит эффективная ширина спектра, определяемая по формуле:

B_k = (Dw/D_max) 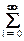D_x(w_i) = Dw×D_x/D_max, (9.2.18)

где D_max - максимальное значение функции D_x(w_i). Отметим, что ширина спектра является практической характеристикой случайного процесса и вычисляется, как правило, для реальных частот по одностороннему спектру процесса. При вычислении по двустороннему спектру, где значение D_max соответственно в два раза меньше, чем в одностороннем спектре, величина B_k завышается в два раза, если суммирование осуществлять по всему спектру. Поэтому пределы суммирования в выражении (9.2.18) не изменяются вне зависимости от того, какой вид спектра используется.

При использовании предельного перехода T Þ ¥ и соответственно интегралов Фурье в выражениях (9.2.15), двусторонние функции дисперсий D(w_i) заменяются функциями S(w), а односторонние - функциями G(w), которые называют соответственно дву- и односторонними функциями спектральной плотности случайных процессов. Такое же индексирование в научно-технической литературе применяют и для спектров ковариационных функций, а зачастую и для дискретных преобразований корреляционных функций вместо D(w_i), хотя последнее применительно к корреляционным функциям более точно отражает физическую сущность величин. Но оно может считаться вполне приемлемым для сохранения общности математических описаний.

Эффективная ширина спектра для функций спектральной плотности случайных процессов:

B_k = 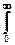G_x(f) df /G_x(f)_max = 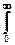S_x(f) df /S_x(f)_max = K_x(0) /S_x(f)_max. (9.2.18')

Соотношение неопределенности связывает эффективную ширину спектра B_k с эффективным интервалом корреляции T_k. Для его определения найдем произведение B_kT_k случайного процесса с использованием формул (9.1.7) и (9.2.18'):

B_kT_k = 2 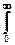|K_x(t)|dt /S_x(f)_max. (8.2.19)

Оценка этого произведения и приводит к соотношению неопределенности:

B_kT_k ³ 1/2. (9.2.20)

Следовательно, с уменьшением эффективной ширины спектра увеличивается эффективный интервал корреляции случайного процесса, и наоборот.

Взаимные спектральные функции.Статистическая связь двух случайных процессов X(t) и Y(t) оценивается по функциям взаимной корреляции K_xy(t) или K_yx(t). Функции взаимной корреляции в общем случае являются произвольными и соответственно функции взаимного спектра представляют собой комплексные выражения:

S_xy(w_i) = (1/T) 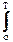K_xy(t) exp(-jw_it) dt, (9.2.21)

при этом:

S_xy(-w) = S_xy^*(w) = S_yx(w).

Квадратурным аналогом нормированной взаимной корреляционной функции или функции коэффициентов корреляции двух процессов (9.1.11) в спектральной области является функция когерентности, которая определяется выражением:

g_xy²(w) = |S_xy(w)|²/(S_x(w)S_y(w)), (9.2.22)

и для любых w удовлетворяет неравенствам

0 £ g_xy²(w) £ 1. (9.2.23)

Функция когерентности обычно используется при анализе линейных систем преобразования входной функции X(t) в выходную функцию Y(t) (рассмотрено ниже).

Теорема Винера-Хинчина. Рассмотрим сигнал q(t), представляющий собой одну реализацию случайного стационарного эргодического процесса длительностью Т. Для сигнала q(t) может быть определен спектр Q(w). Если сдвинуть на t реализацию процесса, то получим спектр Q(w)exp(jwt). Для вещественных сигналов Q(w) = Q*(w) равенство Парсеваля по энергии взаимодействия двух сигналов

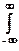x(t) y*(t) dt = 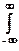X(f) Y*(f) df.

может быть записано в следующей форме:

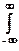q(t)q(t+t) dt = (1/2p) 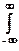Q(w)Q*(w) exp(jwt) dw.

Поделим обе части данного равенства на Т и перейдем к пределу при Т Þ ¥, при этом в его левой части мы увидим выражение для функции ковариации, а в правой части - преобразование Фурье спектра мощности сигнала:

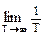
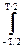q(t)q(t+t) dt =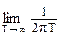 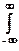|Q(w)|² exp(jwt) dw,

R(t) = (1/2p) 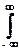W(w) exp(jwt) dw. (9.2.24)

Отсюда следует, что ковариационная функция случайного стационарного эргодического процесса представляет собой обратное преобразование Фурье его спектра мощности, и наоборот:

W(w) = 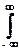R(t) exp(-jwt) dt. (9.2.25)

В этом состоит суть теоремы Винера-Хинчина. Функции W(w) и R(t) являются четными, а соответственно в тригонометрической форме:

R(t) = 2 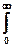W(f)cos(2pft) df, W(f) = 2 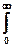R(t)cos(2pft) dt.

Так как корреляционные функции стационарных процессов являются частным случаем ковариационных функций, то эти выражения действительны и для ФАК, а следовательно спектральные функции случайных процессов, рассмотренные выше как преобразования Фурье корреляционных функций, являются спектрами мощности флюктуирующей составляющей процессов. С этих позиций дисперсия случайных процессов представляет собой среднюю мощность его флюктуаций

K(t=0) = s² = (1/2p) 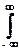W(w) dw,

т.е., равна суммарной мощности всех его частотных составляющих процессов.

В заключение данного раздела отметим, что спектральные плотности процессов и спектры плотности мощности, это одно и то же понятие. Оба термина используются достаточно широко в научно-технической литературе. Учитывая то обстоятельство, что понятие мощности по своему смыслу больше связано с энергетическими понятиями, а понятие спектральной плотности - с анализом сигналов и систем, при дальнейшем рассмотрении случайных сигналов и процессов будем использовать, в основном, понятие спектральной плотности или (для дискретных величин) спектров случайных сигналов и процессов.

9.3. Преобразования случайных функций [л31,л2,л32].

Системы преобразования случайных функций.Пусть имеется система преобразования с одним входом, на который поступает (подается) входная случайная функция X(t) - функция воздействия или возбуждения, и с одним выходом, с которого снимается выходная функция Z(t) - – отклик или выходная реакция системы. Система осуществляет преобразование X(t) Þ Z(t) и описывается определенным системным оператором трансформации Т - функцией, алгоритмом, набором правил преобразования входного сигнала в выходной. Символическое обозначение операции преобразования:

Z(t) = T[X(t)].

При выполнении преобразования конкретных реализаций случайного процесса может использоваться также более информативное символическое отображение операции преобразования:

z(t) = h(t) _* x(t-t),

где h(t) - математическая функция импульсного отклика системы на единичное входное воздействие. Последнее выражение, по существу, представляет собой краткую запись операции свертки, которой реализуется линейное преобразование. В интегральной форме:

z(t) = 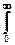h(t)×x(t-t) dt.

Импульсный отклик определяет соответствующую частотную передаточную характеристику системы: h(t) ó H(w).

Для неслучайных (детерминированных) входных сигналов соотношение между выходными и входными сигналами всегда однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса (случайного сигнала) тоже существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии, корреляционной функции и пр.).

Линейные и нелинейные системы составляют два основных класса систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом.

Основные системные операции линейных систем, из которых могут быть сформированы любые линейные операторы преобразования, это операции скалярного умножения, сдвига и сложения сигналов:

s(t) = c ´ a(t), s(t) = a(t-Dt), s(t) = a(t)+b(t).

Для нелинейных систем выделим важный тип безинерционных операций нелинейной трансформации сигнала, результаты которой зависят только от его входных значений. К ним относятся, например, операции квадратирования и логарифмирования сигнала:

y(t) = [s(t)]², y(t) = log[s(t)].

Система считается линейной, если ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).

Принцип аддитивности требует, чтобы реакция на сумму двух входных сигналов была равна сумме реакций на каждый сигнал в отдельности:

T[a(t)+b(t)] = T[a(t)]+T[b(t)].

Принцип однородности или пропорционального подобия требует сохранения однозначности масштаба преобразования при любой амплитуде входного сигнала:

T[c ´ a(t)]= c ´ T[a(t)].

Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.

Примеры линейных операций преобразования:

1. Умножение на заданную функцию: Z(t) = f(t)×Y(t).

2. Дифференцирование: Z(t) = dX(t)/dt.

3. Интегрирование: Z(t) = 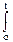X(v) dv.

Линейные системы могут быть неоднородными, если они осуществляют какое-либо линейное однородное преобразование с прибавлением (вычитанием) заданной функции, т.е. операцию вида Z(t) = T[X(t)] = T_o[X(t)] + f(t).

Двухвходовая система описывается системным оператором Т, который связывает два входных воздействия, соответственно X(t) и Y(t), с выходной реакцией Z(t). Система считается линейной, если принципы аддитивности и однородности выполняются для обоих входов, т.е.:

Z(t) = T[c×X(t), c×Y(y)] = c×T[X(t),Y(t)],

Z(t) = T[X₁(t)+X₂(t), Y₁(t)+Y₂(t)] = T[X₁(t),Y₁(t)]+T[X₂(t),Y₂(t)].

Двухвходовая система может применяться, например, для суммирования двух случайных процессов с разными коэффициентами усиления их значений.

При выполнении линейного преобразования Z(t) = T[X(t)] обычно ставится задача определения характеристик распределения Z(t) по известным характеристикам X(t).

Математическое ожидание выходного сигнала:

m_z(t) = M{Z(t)} = M{T[X(t)]}.

Из теории линейных систем: Линейный оператор можно выносить за знак математического ожидания. Отсюда следует:

m_z(t) = T[M{X(t)}] = T[m_x(t)], (9.3.1)

т.е. для определения функции математического ожидания выходного сигнала Z(t) достаточно выполнить преобразование тем же системным оператором функции математического ожидания входного сигнала X(t):

m_z(t) = h(t) _* m_x(t-t). (9.3.2)

Ковариационная функция выходного сигнала:

R_z(t₁,t₂) = M{Z(t₁)Z(t₂)}= M{T₁[X(t₁)]}T₂[X(t₂)]},

где Т₁ и Т₂ - один и тот же оператор Т по переменным соответственно t₁ и t₂, что позволяет вынести его за знак математического ожидания, сохраняя переменные:

R_z (t₁,t₂) = T₁T₂[M{X(t₁)X(t₂)}] =T₁T₂[R_x (t₁,t₂)], (9.3.3)

т.е. при известной функции ковариации входного сигнала функция ковариации выходного сигнала находится двойным преобразованием тем же оператором по двум аргументам.

При определении функции R_z(t) следует учесть порядок преобразования. Для произведения выходных сигналов z(t) и z(t+t) линейной системы можно записать:

z(t)×z(t+t) = 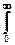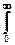h(a)h(b) x(t-a) x(t+t-b) da db.

Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в подынтегральном выражении

M{x(t-a) x(t+t-b)} = -R_x(t-a-t-t+b) = R_x(t+a-b),

получим:

R_z(t) = 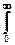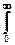h(a)h(b) R_x(t+a-b) da db º R_x(t) _* h(t+a) _* h(t-b). (4.3.4)

Таким образом, функция ковариации выходного сигнала равна функции ковариации входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом системы, что сохраняет четность ковариационной функции выходного сигнала. Аналогичное заключение действительно и для корреляционных функций.

Заметим, что для свертки импульсных откликов, производя замену t-b = t, мы имеем равенство:

h(t+a) _* h(t-b) = h(t+a+b) _* h(t) = h(t) _* h(t+g) = R_h(t),

где R_h(t) - функция ковариации импульсного отклика системы. Отсюда:

R_z(t) = R_x(t) _* R_h(t). (9.3.5)

т.е. функция ковариации выходного сигнала равна свертке функции ковариации входного сигнала с функцией ковариации импульсного отклика системы. Это означает появление в случайном сигнале на выходе системы определенной корреляционной зависимости, вызванной инерционностью системы, причем радиус корреляции выходного сигнала обратно пропорционален верхней частоте, пропускаемой системой.

Функции взаимной ковариации входного и выходного сигналов определяются аналогично:

R_zx (t₁,t₂) = T₁[R_x(t₁,t₂)], R_xz(t₁,t₂) = T₂[R_x(t₁,t₂)]. (9.3.6)

Для функции R_xz входного и выходного сигналов имеем:

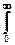x(t)×z(t+t) dt =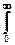 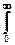h(a) x(t) x(t+t-a) da dt.

R_xz(t) = 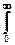h(a) R_x(t-a) da º R_x(t) _* h(t-a). (9.3.7)

т.е. функция взаимной ковариации входного и выходного сигналов равна свертке функции ковариации входного сигнала с функцией импульсного отклика системы.

Другая взаимно ковариационная функция R_yx может быть получена из соотношения:

R_zx(t) = R_xz(-t) º R_x(t) _* h(t+a). (9.3.8)

Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике h(t) = 0 при t<0 функция R_xz(t) также является односторонней и равна 0 при t<0, а функция R_zx соответственно равна 0 при t>0.

Спектральные соотношения,которые характеризуют систему в целом по отношению к преобразованию случайных сигналов, это соотношения спектральных плотностей случайных сигналов (спектров мощности) на входе и выходе.

Применяя преобразование Фурье к выражениям (9.3.5), для спектра мощности выходного сигнала получаем:

S_z(f) = S_x(f) |H(f)|². (9.3.9)

Спектр мощности случайного сигнала на выходе системы равен спектру мощности входного сигнала, умноженному на квадрат модуля частотной характеристики фильтра. С учетом четности корреляционных функций спектр мощности выходного сигнала также является четной действительной функцией и содержит только амплитудную характеристику системы.

Аналогично, для взаимного спектра мощности сигналов на основе выражений (9.3.7-8) имеем:

S_xz(f) = S_x(f) H(f). (9.3.10)

S_zx(f) = S_x(f) H(-f). (9.3.10')

Взаимный спектр сигналов при одностороннем импульсном отклике является комплексным и содержит как амплитудную, так и фазовую характеристику системы.

Отметим, что с использованием выражения (9.3.10) можно производить определение частотной характеристики и импульсного отклика системы:

H(f) = S_xz/S_x Û h(t).

Дисперсия выходного сигналаможет быть определена с использованием формул (9.3.4,9) по функциям корреляции:

s_z ² = K_z(0) = 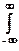S_x(f) |H(f)|² df º K_x(0) 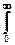h²(t) dt = s_x² 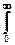h²(t) dt, (9.3.11)

Если сигнал нецентрированный и значение дисперсии <