Пример расчета фильтра низких частот Баттеруорта.

Начиная с этого параграфа, будем сопровождать рассмотрение теории последовательным расчетом конкретного фильтра низких частот с применением приводимых формул. Для расчета примем следующие исходные параметры фильтра:

- Шаг дискретизации данных Dt = 0.0005 сек.

Частота Найквиста f_N = 1/2Dt = 1000 Гц, ω_N = 6.283·10³ рад.

- Граничная частота полосы пропускания: f_p = 300 Гц, w_p = 1.885·10³ рад.

- Граничная частота полосы подавления: f_s = 500 Гц, w_s = 3.142·10³ рад.

- Коэффициенты неравномерности: А_р = А_s = 0.1.

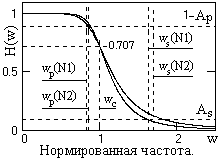Рис. 6.1.2.

Расчет дополнительных параметров:

1. Значение d по формуле (6.1.3) или по ее эквиваленту

d = A_p 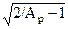/(1-A_p): d= 0.484.

2. Деформированные частоты по формуле (6.1.4):

w_dp = 2.038·10³ рад.

w_ds = 4·10³ рад.

3. Порядок фильтра по формуле (6.1.6): N = 4.483.

Для пояснения дальнейшего порядка расчетов при четном и нечетном порядке фильтра, принимаем N1=4, N2=5.

4. Частота среза фильтра по формуле (6.1.7):

w_dc(N1) = 2.443·10³ рад (389 Гц),

w_dc(N2) = 2.356·10³ рад (375 Гц).

5. По формуле H(w) = 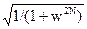, w = ω/ω_dc, для контроля строим графики передаточных функций (рис.6.1.2).

Функция |H(W)|² – представляет собой энергетический спектр сигнала (спектральную плотность мощности) и не имеет фазовой характеристики, т.е. является четной вещественной, образованной из двух комплексно сопряженных функций H(W) и H*(W), при этом порядок фильтра N определяет число полюсов функции H(W) и комплексно сопряженных с ними полюсов функции H*(W).

Преобразование Лапласа. Переводим функцию |H(W)|² на координатную ось пространства преобразования Лапласа при p = jW, для чего достаточно подставить W = p/j:

|H(р)|² = 1/[1+(p/j)^2N]. (6.1.8)

Полюсы функции находятся в точках нулевых значений знаменателя:

1+(p/j)^2N = 0, p = j 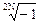. (6.1.9)

Отсюда следует, что полюсы располагаются на единичной окружности в p-плоскости, а их местоположение определяется корнями уравнения (6.1.9). В полярных координатах:

p_n = j exp(jp(2n-1)/2N), n = 1,2, ... ,2N. (6.1.10)

p_n = j cos[p(2n-1)/2N] - sin[p(2k-1)/2N]. (6.1.10')

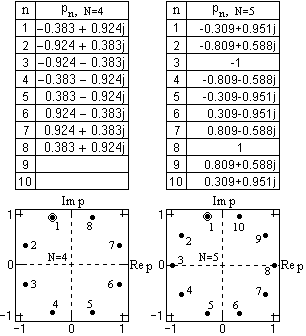Рис. 6.1.2.