РЕЖИМИ РУХУ МЕХАНІЗМУ

Робота механізму (або машини) має три характерні періоди руху:

а) період розбігу;

б) період усталеного руху;

в) період вибігу.

За період розбігу (пуску машини) швидкість руху початкової ланки зростає від нуля (v₀ = 0) до деякої середньої (робочої) швидкості (v = v_р). Рівняння руху механізму в енергетичній формі набуває вигляду

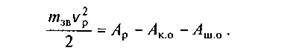
Оскільки то для періоду пуску механізму справедлива така нерівність:

З цього випливає, що в період пуску механізму робота рушійних сил має бути більшою за суму робіт сил корисного і шкідливого опору. Надлишок роботи A_р витрачається на збільшення кінетичної енергії механізму, тобто збільшення швидкості рухомих мас.

Часто для скорочення часу пуску машини знімають з неї корисне навантаження (Ако = 0). Рух машини без корисного навантаження називають холостим ходом машини.

При усталеному русі машини швидкість початкової ланки головного вала) механізму чи машини коливається навколо середнього значення, яке відповідає робочій швидкості цієї ланки. Проміжок часу, по закінченні якого положення, швидкості й прискорення початкової ланки механізму набувають початкового значення, називають періодом зміни кінетичної енергії механізму або циклом t_ц усталеного руху.

Швидкості початкової ланки на початку і в кінці циклу усталеного руху рівні між собою v₀ = v_p). Тоді рівняння руху набуває вигляду

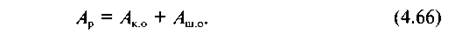
Отже, при усталеному русі механізму (машини) робота рушійних сил за один цикл дорівнює сумі робіт корисного і шкідливого опору. У середині циклу ця рівність може не зберігатись, а тому мають місце коливання швидкості початкових ланок механізму. Очевидно, коли А_р > А_ко + А_шо, рух механізму буде прискорений і, навпаки, коли А_р < А_ко + А_шо, рух сповільнений, тому в обох випадках умова v_p = const буде порушена.

При вибігу (зупинці) машини насамперед треба зупинити подачу рушійної енергії машини (відключити двигун), тобто A_p = 0. Кінцевим станом машини буде спокій, при якому швидкість початкової ланки v = 0, а початкова швидкість v_o = v_р. Для цього випадку рівняння руху машини набуває вигляду

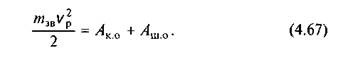
З рівняння (4.67) видно, що зупинка машини буде досягнута тільки тоді, коли вся нагромаджена машиною кінетична енергія рухомих мас поглинається роботою сил корисного і шкідливого опору.

На практиці для скорочення часу зупинки машини дуже часто штучно збільшують роботу сил шкідливого опору за допомогою установки гальм.

Таким чином, у період розбігу кінетична енергія машини збільшується за рахунок надлишку роботи рушійних сил над роботою сил опору (А_р > А₀); у період усталеного руху кінетична енергія на початку і в кінці кожного циклу (періоду) однакова (А_p = А₀) нарешті, у період вибігу кінетична енергія повністю поглинається роботою всіх сил опору.

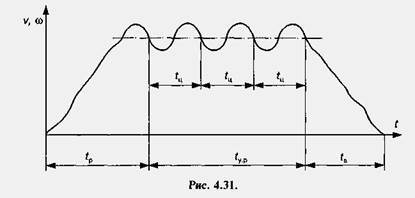
На рис. 4.31 показано приклад залежності швидкості руху початкової ланки механізму від часу . Час усталеного руху залежить від часу одного циклу t_ц і кількості циклів k (t_ур = kt_ц). Кількість циклів визначається технологічним процесом, який виконує машина. Слід зазначити, що цикл роботи механізму (машини) не завжди відповідає одному оберту початкової ланки. Так, наприклад, у чотиритактному двигуні внутрішнього згоряння протягом циклу колінчастий вал двигуна робить два оберти.

Багато машин, механізмів і приладів (вантажопідіймальні машини, екскаватори, реле, контактори і т. п.) не працюють у режимі усталеного руху, їх рух, як правило, складається з розбігу й вибігу.

1.2. МЕХАНІЧНИЙ КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ

З рівняння руху механізму для періоду усталеного руху видно, що А_р = А_ко + А_шо, тобто вся енергія рушійних сил, яка витрачається в машині, поділяється на дві частини: одна частина йде на перемагання сил виробничих (корисних) опорів, друга — на перемагання шкідливих опорів (сил тертя, опору середовища). Механізм або машина вважається тим досконалішими, чим більша частина енергії (за однакових інших умов), що підводиться до них, йде на перемагання корисних опорів. Ефективність використання енергії в машині характеризується так званим механічним коефіцієнтом корисної дії (ККД).

Механічним ККД з називають відношення роботи сил корисного опору до роботи рушійних сил за цикл усталеного руху, тобто

У реальних машинах механічний ККД завжди менший за одиницю. Це пояснюється тим, що робота сил корисного опору завжди менша за роботу рушійних сил. Дійсно, з рівняння (4.66) видно, що А_ко = А_р - А_шо, а оскільки робота сил шкідливого опору не дорівнює нулю (А_шо ≠ 0), то А_ко < А_р і η < 1.

Залежність (4.68) можна записати також у такому вигляді:

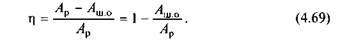
Відношення роботи сил шкідливого опору до роботи рушійних сил прийнято називати механічним коефіцієнтом втрат ψ. Відповідно до цього (4.69) можна записати так:

З (4.69) випливає, що механічний ККД може дорівнювати нулю, якщо робота рушійних сил дорівнює роботі всіх невиробничих опорів, які є в механізмі. За такої умови рух механізмів можливий, але без виконання будь-якої корисної роботи. Такий рух механізму називають холостим рухом. ККД не може бути меншим від нуля, оскільки для цього необхідно, щоб відношення робіт А_шо І А_р було більше від одиниці, тобто А_шо > А_р. У таких випадках настає самогальмування машини або механізму.

Отже, ККД машини або механізму може змінюватися в межах

Тоді з рівнянь (4.70) і (4.71) випливає, що коефіцієнт втрат змінюється в межах 0 < ψ < 1.

Слід зауважити, що механічний коефіцієнт корисної дії і коефіцієнт втрат не дають повної характеристики машини, а також інформації про її продуктивність, безпеку праці, вартість, якість продукції, яку вона випускає. Вони характеризують тільки ефективність використання енергії. ККД і коефіцієнт втрат придатні тільки для порівняння машин і пристроїв однакового призначення. У деяких машинах корисне навантаження дуже мале (наприклад, у поліграфічних і текстильних машинах, машинах швейної промисловості тощо), тому й ККД невеликий.

ККД і коефіцієнт втрат можна виразити і через відношення відповідних потужностей.

Під час руху машини ККД і коефіцієнт втрат не залишаються сталими, тому що під час руху машини змінюються зусилля, які діють на ланки машин, а значить, змінюються сили тертя і робота сил шкідливого опору (робота сил корисного опору також може змінюватися). На практиці, як правило, обмежуються визначенням середнього значення ККД для якого-небудь проміжку часу, найчастіше для одного циклу періоду усталеного руху. Такий ККД називають цикловим. При обчисленні ККД для даного положення механізму дістаємо миттєвий коефіцієнт корисної дії.

Для кожної машини існує деяка найвигідніша швидкість, при якій її ККД досягає максимального значення. Вищий ККД мають механізми і машини з чисто обертовим рухом ланок — ротаційні машини. Машини зі зворотно-поступальним рухом ланок — поршневі машини, механізми періодичної дії, мають здебільшого низький ККД через несприятливу дію динамічних сил (сил інерції).

1.3. КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ МАШИНИ

Як правило, сучасні машини складаються з багатьох механізмів, ККД яких відомі або його можна порівняно легко знайти. Проте загальний ККД машини залежить не тільки від ККД окремих механізмів, що входять до її складу, але й від способу з'єднання цих механізмів у машині. Відрізняють три способи з'єднання механізмів у машині: послідовне, паралельне і змішане.

Послідовне з'єднання механізмів. Нехай є машина, яка складається з з послідовно з'єднаних механізмів (рис. 4.32), кожен з яких має відповідно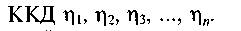

Загальний ККД такої машини визначається за формулою

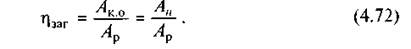
Перший механізм приводиться в рух рушійними силами, що ви­конують роботу А_р. Оскільки корисна робота А₁ першого механізму буде роботою рушійних сил для другого механізму і відповідно у всьому ланцюгу механізмів корисна робота кожного попереднього механізму буде роботою рушійних сил для кожного наступного механізму, то коефіцієнт корисної дії кожного механізму обчислюється так:

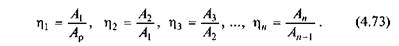
Якщо перемножити між собою ліві та праві частини (4.73), дістанемо

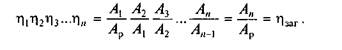
Отже, загальний механічний ККД послідовно сполучених механізмів (або машин) дорівнює добуткові механічних ККД окремих механізмів (або машин),

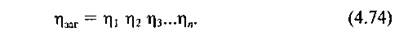що утворюють одну машину (або машинний агрегат), тобто

З формули (4.74) видно, що чим складніша машина, тим більші втрати енергії і тим менший ККД. Причому загальний ККД машини при послідовному з'єднанні механізмів завжди менший за найменший ККД механізмів, які входять до його складу 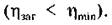Це свідчить про те, що при послідовному

з'єднанні механізмів необхідно дуже старанно виготовляти кожний механізм, кожний вузол машини, інакше не можна домогтися високого ККД машини.

Паралельне з'єднання механізмів. На рис. 4.33 показано схему машини з паралельним з'єднанням механізмів. Робота рушійних сил А_р, яка підводиться до машини, розподіляється між окремими механізмами відповідно А₁, А₂, А₃, ..., А_n, які є для кожного механізму рушійними роботами, а значить,

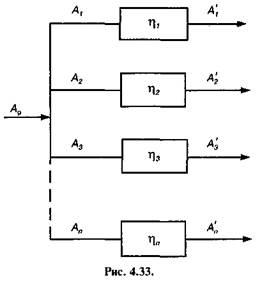
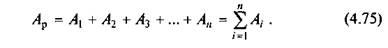
Кожний механізм відповідно виконує корисну роботу:

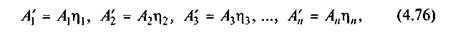
де η_i— ККД i-го механізму.

Загальна корисна робота всієї машини дорівнює сумі робіт усіх механізмів, тобто

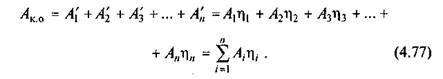
Тоді на основі (4.68) загальний ККД машини при паралельному з'єднанні механізмів має вигляд

З формули (4.78) випливає, що механічний ККД машини при паралельному з'єднанні механізмів залежить не тільки від ККД окремих механізмів, але й від характеру розподілу роботи рушійних сил між механізмами. Очевидно, чим більша частина всієї затраченої роботи поступатиме в механізм з найбільшим ККД, тим значення ККД усієї машини буде більшим, і, навпаки, ККД машини буде тим меншим, чим більша частина Ар надходитиме в механізм з найменшим ККД.

Цікаві окремі випадки ККД машини при паралельному з'єднанні механізмів. Зокрема, якщо роботу рушійних сил А9 розподілити рівномірно між механізмами 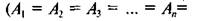= А), то ККД машини (4.78) матиме вигляд

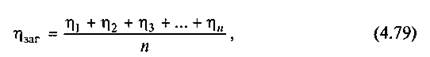
де n — число механізмів.

З формули (4.79) видно, що загальний ККД машини при паралельному з'єднанні механізмів дорівнює середньому значенню ККД механізмів, які входять до складу машини. Очевидно, що η_заг при паралельному з'єднанні механізмів не може бути меншим за найменший і більшим за найбільший ККД складових механізмів (η_min≤η_заг ≤η_max ). При паралельному з'єднанні низький ККД одного механізму менше впливає на значення ККД машини, ніж при послідовному з'єднанні механізмів.

Якщо у випадку, який розглянуто залежністю (4.79), прийняти ККД усіх механізмів однаковими (η₁= η₂ = η₃ = ... = η₄ = =η_м загальний ККД машини дорівнюватиме ККД окремого механізму (η_заг = η_м).

При складному (змішаному) з'єднанні механізмів для визначення ККД машини користуються загальною формулою (4.68). Остаточні формули ККД машини залежать від схеми сполучення механізмів, в якій завжди можна виділити послідовні та паралельні ланцюги з'єднаних між собою механізмів.

4.14. ЗАГАЛЬНІ МЕТОДИ ДОСЛІДЖЕННЯ РУХУ МЕХАНІЗМУ

Для визначення закону руху початкової ланки механізму, яка визначає рух усіх інших ланок, використовують рівняння руху (4.57), (4.58) або (4.63), (4.64). Розв'язуючи їх відносно швидкості руху початкової ланки, встановлюємо характер зміни її руху залежно від часу. Для цього здебільшого використовують диференціальні рівняння (4.63), у ліві частини яких входить зведений момент сил М_зв, що є сумою зведених моментів рушійних сил М_р і сил опору М₀, тобто М_зв = М_р + М₀. Як було показано (див. параграф 4.3), ці моменти можуть бути функціями узагальненої координати φ або її першої похідної 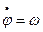, або, нарешті, часу t.

Якщо розглянути можливі комбінації цих функцій, то можна встановити такі види рівнянь, в яких моменти М_р і М₀ є функціями однієї й тієї самої змінної .

Перший вид рівнянь має вигляд

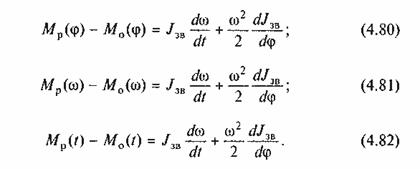
У рівняннях (4.80) — (4.82) моменти М_р рушійних сил і моменти М₀ сил опору в кожному з рівнянь є функціями або φ, або ω, або t. Проте часто трапляються випадки, коли М_р і М₀ є функціями різних змінних. Тоді дістанемо рівняння другого виду

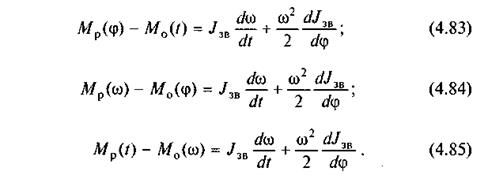
Рівняння (4.80)—(4.85) у загальному випадку є нелінійними диференціальними рівняннями, розв'язати які можна тільки наближеними методами.

Можна побачити, що тільки рівняння (4.80) може бути розв'язане, і причому в квадратурах, а не в скінченному вигляді.

Дійсно, якщо М_р = М_р(φ) і, М_о = М_о(φ) то згідно з рівнянням (4.62) рівняння (4.80) можна записати в такій формі:

звідки маємо

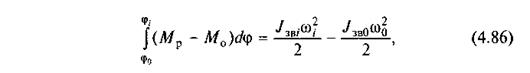де 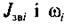— зведений момент інерції і кутова швидкість ланки

зведення у положенні і; 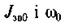— зведений момент інерції і кутова швидкість ланки зведення в початковому положенні. Рівняння (4.86) є рівнянням руху механізму у формі рівняння кінетичної енергії.

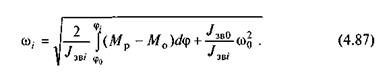З рівняння (4.86) визначається кутова швидкість у положенні і:

З цієї формули випливає, що якщо задані функції Мр =

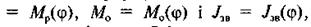то для визначення кутової швидкості ω, необхідно ще мати задане значення кутової швидкості ω₀. Якщо дослідження руху механізму починаються з моменту пуску його в хід, то кутова швидкість (ω₀ = 0 і формула (4.87) набуває вигляду

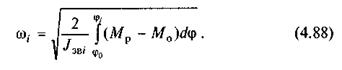
З формул (4.87) і (4.88) можна визначити значення кутової швидкості ланки зведення у функції її кута повороту, тобто ω= ω(φ).

Для визначення часу t руху механізму можна скористатися умовою

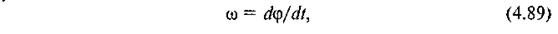
звідки дістанемо

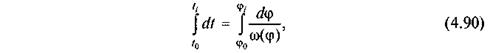
або

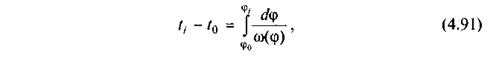
і далі

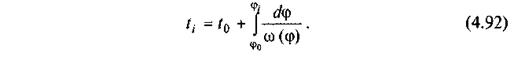
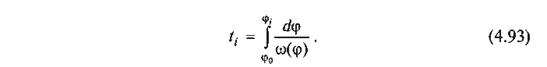Якщо дослідження руху механізму ведеться з початку пуску його в хід, то t₀ = 0 і рівняння (4.92) набуває вигляду

З формул (4.92) або (4.93) можна визначити час і руху механізму як функцію кута ц повороту ланки зведення, тобто t=t(φ). Таким чином, маємо дві функції: ω = ω (φ) і t = t (φ). Якщо виключити з них кут φ, можна дістати функцію ω = ω (t) — залежність кутової швидкості ω від часу t. Кутове прискорення ε ланки зведення визначається із співвідношення

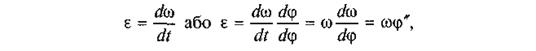
де 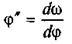— аналог кутових прискорень ланки зведення.

В окремих випадках, коли зведений момент інерції I_зв сталий, формули (4.86) і (4.87) набувають вигляду

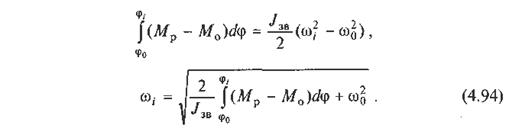
Якщо задано не зведені моменти, а зведені сили F_p = F_p(s), F₀ = F₀(s) і зведена маса m_зв = m_зв (s), де s — переміщення (шлях) точки зведення, то рівності, що здобуті при розв'язанні рівняння руху, будуть аналогічні рівнянням (4.86) і формулам (4.87), (4.92).

В окремих випадках рівняння (4.81) і (4.82) можна розв'язати в квадратурах, якщо зведені моменти інерції сталі (I_зв= = const). Тоді рівняння (4.81) матиме вигляд

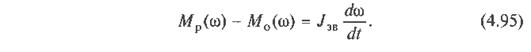
Оскільки моменти М_р = M_р(ω) і М₀ = М₀(ω) задані і відомий момент інерції I_зв, то рівняння (4.95) можна записати в такому вигляді:

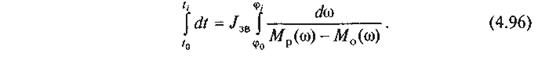
З рівняння (4.96) визначаємо час t руху механізму як функцію кутової швидкості, тобто t = t(ω). Якщо проінтегруємо ліву частину, то дістанемо

Рівняння (4.82) при I_зв = const зводиться до вигляду

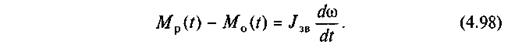
Оскільки моменти М_р = М_р(t) і М₀ = M₀(t) - задані і відомий момент інерції I_зв, то з рівняння (4.98) маємо

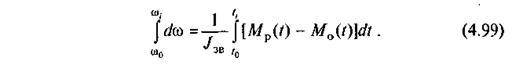
З цього рівняння визначаємо кутову швидкість ω, руху ланки зведення у функціях часу t:

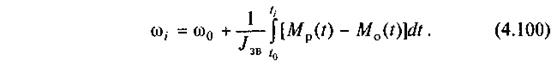
Одержати розв'язок рівнянь (4.83)—(4.85) у скінченному вигляді можна для окремих випадків, коли функції, які знаходяться в лівій частині цих рівнянь, досить прості.

У загальному випадку, як про це вже йшлося вище, рівняння (4.80)—(4.85) можуть бути проінтегровані наближеними методами. Таким методом, зокрема, може бути метод, запропонований Г. Г. Барановим, який полягає в тому, що кут повороту φ ланки зведення розбивається на досить малі інтервали ∆φ, які беруться за крок інтегрування. У кожному інтервалі ∆φ задані функції зведених моментів рушійних сил М_р і сил опору М₀ вважаються сталими, а зведений момент інерції I_зв змінюється лінійно.

Позначимо ліві частини рівнянь (4.80)—(4.85) узагальнено у вигляді М(φ, ω, t), оскільки моменти M_р і М₀ можуть бути функціями кута повороту φ , кутової швидкості ω і часу t .

Тоді ці рівняння можна записати в загальному вигляді так:

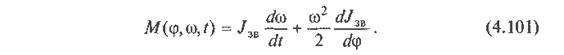
Оскільки

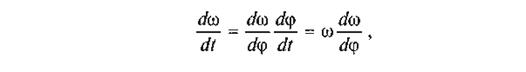
рівняння (4.101) можна записати в такому вигляді:

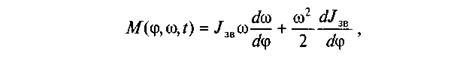
або

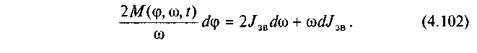
Замінюємо в рівнянні (4.102) dφ кроком інтегрування 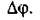Тоді величину dω приросту швидкості можна замінити різницею 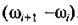, а величину dJ_3B приросту зведеного моменту інерції — різницею 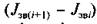, де i та i + 1 — два положення ланки зведення, що відповідають початку і кінцю інтервалу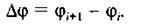

З урахуванням викладеного рівняння (4.102) матиме вигляд

Розв'язуючи це рівняння відносно кутової швидкості щ,+1, дістанемо

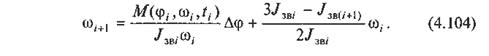
Знаючи значення для 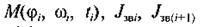і ω_i, з формули

(4.104) при вибраному кроці інтегрування ∆φ , можна визначити кутову швидкість ω_i+1. Виконуючи крок за кроком обчислення кутової швидкості ω, дістаємо функцію ω = ω (φ).

Для визначення часу t руху ланки зведення можна використати умову

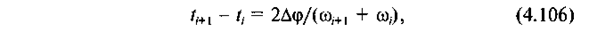Замінимо в цьому рівнянні dt на різницю t_i+l - t_i , dφ — на крок ∆φ інтервалу і кутову швидкість ω — на її середнє значення 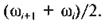У цьому разі можна записати

звідки визначаємо час в положенні i+ 1:

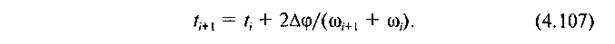
Такий метод наближеного інтегрування можна використати як при аналітичному, так і при графічному зображенні всіх функцій, що входять у рівняння (4.80)—(4.85).