Тертя в поступальних кінематичних парах

ТЕРТЯ В МЕХАНІЗМАХ

Під час руху одного тіла відносно іншого між поверхнями, що стикаються, виникає взаємодія, яка перешкоджає переміщенню цього тіла, а якщо воно знаходиться в стані спокою, — його відносному зміщенню. Це явище називається тертям, а сили опору — силами тертя. Отже, тертям називають опір, що виникає при переміщенні одного тіла відносно іншого. Поверхні, якими стикаються між собою тіла, називаються тертьовими.

Виникнення тертя пояснюється двома основними причинами. По-перше, поверхні тертя не абсолютно гладкі, а мають нерівності, які при стиканні поверхонь створюють опір руху Ff (рис. 6.1). По-друге, між тілами, які стикаються поверхнями, виникають сили молекулярної взаємодії, для подолання яких також необхідно прикласти силу. Як показують експериментальні дослідження, тертя є складний комплекс механічних, фізичних і хімічних явищ, причому ті чи інші явища переважають залежно від умов, за яких проходить процес тертя.

Тертя є одним із найпоширеніших явищ природи і відіграє дуже важливу роль у техніці. Цілий ряд задач механіки, деталей машин, спеціальних технічних дисциплін не можна розв'язати без знань законів тертя. На використанні сил тертя грунтується робота багатьох машин і механізмів (пасової і фрикційної передач, транспортних машин, прокатних станів, фрикційних муфт, гальм тощо). Великі сили тертя виникають при обробці металів різанням.

Тертя відіграє в машинах як корисну, так і шкідливу роль. З одного боку, завдяки тертю рухаються тіла; з другого — тертя є причиною зношування деталей машин і приладів, значних витрат енергії. Підраховано, що близько 1/3 світових енергетичних ресурсів даремно витрачаються на роботу, пов'язану з тертям.

Відомо, що перші дослідження явища тертя проводив ще Леонардо да Вінчі. Детальне дослідження законів тертя почав французький механік і фізик Г. Амонтон (1663—1705) і протягом усього століття ці дослідження поглиблювалися. В 1781 р. ПІ. Кулон опублікував працю "Теорія простих машин з точки зору їх частин...", в якій розвинув теорію тертя, сформулював основні закони тертя. Експериментальне дослідження тертя продовжували і послідовники Кулона. Проте треба зауважити, що ця складна наукова проблема і до нашого часу повністю не розв'язана. Тому на практиці все ще користуються наближеними емпіричними законами, які були відкриті Амонтоном і Кулоном. Якщо треба мати більшу точність розрахунків, то доводиться визначати силу тертя експериментально для кожної пари тертьових поверхонь і конкретних умов тертя.

Власне кажучи, вивчення всіх особливостей теорії тертя виходить за межі курсу теорії механізмів і машин. Тут розглядатимемо лише ті елементи цієї теорії, які необхідні, щоб точніше визначити вплив тертя на реальні значення сил, що діють на тіла, встановити умови їх рівноваги, врахувати сили тертя при розв'язанні тих чи інших інженерних задач, в яких неможливо ними знехтувати.

Види тертя

Залежно від характеру відносного переміщення тіл, що стикаються, відрізняють два види тертя: ковзання і кочення. Інколи розглядають ще один вид тертя — так зване тертя вертіння. При терті ковзання одні і ті самі поверхні одного тіла стикаються з різними поверхнями іншого тіла. При терті кочення різні поверхні одного тіла послідовно стикаються з різними поверхнями іншого тіла.

Прикладами тертя ковзання можуть бути тертя лиж по снігу, пили по дереву, різця по металу, підошви взуття по землі, цапфи вала по втулці підшипника тощо. Тертя кочення має місце при перекочуванні коліс автомобіля по землі або вагона по рейках, у шарикових або роликових підшипниках, фрикційних передачах тощо.

Для зменшення сил тертя використовують різні мастила. Залежно від їх наявності між тертьовими поверхнями розрізняють два основних види тертя: сухе тертя (без мастильних матеріалів) і рідинне тертя (з мастильними матеріалами). При сухому терті між тертьовими поверхнями

 

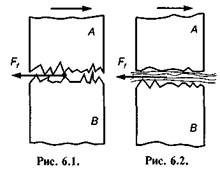тіл відсутнє будь-яке мастило. При рідинному терті тертьові поверхні тіл повністю розділені шаром мастила (рис. 6.2) і тертя твердих частин тіла замінено тертям окремих шарів мастила. Мастило може бути твердим, рідким або газоподібним.

Крім цього, інколи ще розрізняють проміжні види тертя: граничне, напівсухе і напіврідинне. При граничному терті на тертьових поверхнях є тонкі адсорбовані маслянисті плівки. Напівсухе і напіврідинне тертя не мають між собою чіткої границі: якщо перевершує сухе тертя (більша частина поверхні контакту не покрита мастилом), то вважають, що тертя напівсухе, і навпаки, якщо перевершує рідинне тертя, то маємо напіврідинне тертя.

Тертя ковзання

Щоб виявити основні закономірності тертя ковзання, можна провести ряд дослідів на досить простому приладі (трибометрі), який схематично зображений на рис. 6.3. На пластину 1, розташовану в заглибленні горизонтального стола, ставимо тіло 2 вагою G. Силу тиску тіла 2 на пластину можна змінювати шляхом зміни його ваги (за допомогою установки гир). Нормальна реакція пластини: N = -G. До тіла 2 прив'яжемо нитку і, перекинувши її через блок 3, підвісимо на її кінці чашку з гирями вагою Q. Щоб зменшити можливість перевертання тіла, нитку прив'яжемо ближче до його основи, і тоді тіло 2 залишається в стані спокою доти, доки модуль сили F = Q не досягне деякого значення, яке цілком визначене для даної пари тертьових поверхонь і даної сили тиску між ними. Це свідчить про те, що на тіло 2, крім нормальної реакції N, з боку пластини 1 діє ще інша реакція Ffi яка за модулем дорівнює горизонтальній силі F і направлена в протилежний від неї бік. Ця реакція, що лежить у дотичній площині, і є сила тертя.

Максимального значення сила тертя Fmm досягає в той момент, коли тіло почне рухатись.

Звідси можна зроби­ти такі висновки: а) сила тертя ковзання виникає тільки при наявності зсувної сили;

б) модуль сили тертя ковзання при рівновазі тіла може набувати різних значень, які не перевищують максимальні, тобто Ff < -Fmax. Цю най 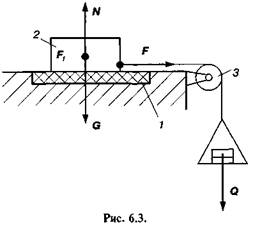більшу силу тертя називають статичною або силою тертя спокою.

Сила тертя, яка перешкоджає ковзанню тіла під час його руху, називається силою тертя руху, або динамічною силою тертя. Як показують досліди, сила тертя руху менша від статичної сили тертя. З практики відомо, що легше підтримувати початий рух, ніж зрушити тіло з місця.

На основі численних дослідів Амонтоном і Кулоном встановлено такі (наближені) закони [4].

1. Сила тертя при однакових інших умовах не залежить від
розмірів тертьових поверхонь. Цей закон можна обгрунтувати за
допомогою таких міркувань. Якщо, наприклад, площа тертьових
поверхонь збільшується, то збільшується і кількість нерівностей
поверхонь, які зчіплюються, але зменшується тиск на одиницю
площі, і сила опору рухові залишається попередньою. Проте
треба мати на увазі, що цей закон наближено справедливий
лише до деяких значень тиску тіла на площину, поки тертьові
поверхні не дуже малі.

2. Максимальне значення сили тертя спокою прямо
пропорційне нормальному тиску (нормальній реакції) одного тіла
на інше в момент початку їх відносного руху, тобто

де /о — коефіцієнт тертя спокою, який можна виразити відношенням

 

Коефіцієнт тертя спокою f0 — величина безрозмірна і є відношенням максимальної сили тертя /^ до нормальної реакції N. Сила нормального тиску дорівнює вазі тіла тільки тоді, коли поверхня ковзання горизонтальна площина і на тіло не діють інші сили, крім сили його ваги. Якщо тіло лежить на похилій площині (рис. 6.4), то нормальна реакція N=Gcosα, де α — кут нахилу площини. Якщо ж на тіло 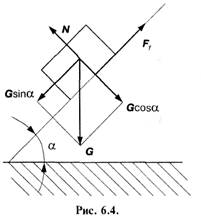крім сили тяжіння діють ще інші сили, то за силу нормального тиску на поверхню треба брати нормальну складову рівнодіючої всіх прикладених до нього сил.

3. Модуль сили тертя в стані рівноваги (спокою) не більший від максимальної сили тертя спокою, тобто

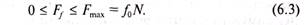
4. Коефіцієнт тертя спокою залежить від матеріалу тіл, що
стикаються, і фізичного стану тертьових поверхонь, тобто від
величини і характеру шорсткості, наявності мастила, вологості,
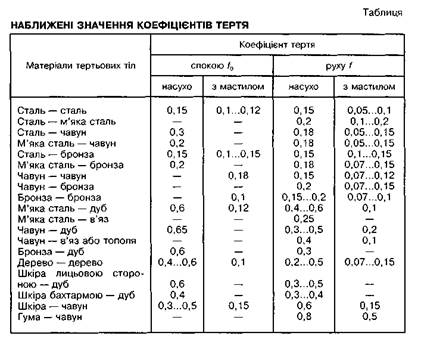
температури та інших умов. Наближені значення коефіцієнтів
тертя спокою наведено в таблиці [76]. Детальніші відомості про
коефіцієнти тертя можна знайти в різних технічних довідниках.
Матеріали, які мають високий коефіцієнт тертя, називають
фрикційними (шкіра, гума, текстоліт, азбест тощо) і, навпаки,
низький коефіцієнт тертя, -- антифрикційними (бронза, бабіт,
сірий чавун, капрон і деякі інші види пластмас).

5. Сила тертя під час руху менша сили тертя в спокої.
Досліди показують, що для того щоб вивести тіло зі стану
спокою, треба при інших однакових умовах прикласти іншу
силу, ніж для підтримки руху. Для більшості матеріалів сила
тертя в русі залежить від швидкості одного тіла відносно іншого
і, як правило, зменшується зі збільшенням цієї швидкості,
прямуючи до певної межі. У деяких випадках, як наприклад,
при терті шкіри по сталі або чавуну, коефіцієнт тертя зростає із
збільшенням швидкості.

6. Сила тертя зростає із збільшенням часу попереднього
контакту тертьових поверхонь. Це,напевно, слід пояснити дефор-

мацією стичних поверхонь, деякою дифузією молекул тертьових тіл, а значить, збільшенням їх молекулярних зв'язків.

Модуль сили тертя під час руху можна визначити за формулою, аналогічною (6.1), підставивши в неї замість коефіцієнта тертя спокою fu коефіцієнт тертя руху/, тобто

Значення коефіцієнта тертя руху наведено також у таблиці.

При наближених інженерних розрахунках часто не роблять різниці між коефіцієнтами тертя спокою і руху, а користуються значеннями коефіцієнтів тертя руху.

Аналіз висунутих Амонтоном і Кулоном положень, зроблений іншими дослідниками, показав, що ці положення можна вважати вірними тільки для певних тертьових матеріалів і деяких границь швидкості і навантажень. Так, на основі ряду експериментів було встановлено [4], що залежність сили тертя від нормального тиску виражається рівністю

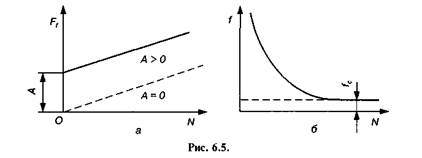
У цьому рівнянні fс є коефіцієнт тертя руху, який для розглядуваних тіл вважаємо сталим, і А — деяка стала сила тертя, яка залежить не від тиску N, а від схильності стичних поверхонь до попереднього зчеплення. Отже, хоч залежність сили тертя від нормального тиску лінійна, закон зміни сили тертя і функції нормального тиску виражається у вигляді прямої, що не проходить через початок координат (рис. 6.5, а).

Стала А характеризує зчіплюваність стикових поверхонь і вказує на необхідність прикладання додаткової сили для подолання попереднього зчеплення стикових поверхонь.

Розділивши обидві частини рівності (6.5) на N, дістанемо

Тут / = Ff / N коефіцієнт тертя, графічне зображення якого показано на рис. 6.5, б, має вигляд гіперболи. Отже, коефіцієнт тертя, взагалі кажучи, залежить від нормального тиску. У технічних розрахунках, як правило, користуються рівнянням Амонтона— Кулона в найпростішій його формі (6.4), нехтуючи зчіплюваністю поверхонь, де під коефіцієнтом тертя розуміють деяке його середнє значення, яке визначається експериментальне і береться сталим. У цьому випадку залежність сили тертя від нормального тиску графічно виражається прямою лінією, що проходить через початок координат (на рис. 6.5, б — штрихова лінія).

Досліди також вказують, що коефіцієнт тертя / змінюється при зміні навантаження на одиницю площі дотику. Отже, основні положення про сили сухого тертя в уточненій формі можна сформулювати так [ 1, 4]:

а) коефіцієнт тертя можна вважати сталим, а сили тертя — прямо пропорційними нормальному тиску тільки в певному діапазоні швидкостей і навантажень;

б) сили тертя завжди направлені в бік, протилежний
відносним швидкостям;

в) тертя спокою в початковий момент руху в більшості випадків дещо більше за тертя руху;

г) із збільшенням швидкості руху сила тертя здебільшого
зменшується, наближаючись до деякого сталого значення;

д) із зростанням питомого тиску сила тертя переважно
збільшується;

е) із збільшенням часу попереднього контакту сила тертя
збільшується.

Кут і конус тертя

Розглянемо ще раз взаємодію тіла, що спирається на негладку поверхню (рис. 6.6, а). Якби поверхні тіл були абсолютно гладкі, то це була б ідеальна в'язь (зв'язок), дія якої на тіло зводилась би лише до нормальної реакції N. Якщо ж опорна поверхня шорстка, то при дії рушійної (активної) сили F з'являється ще й сила тертя, яка лежить у дотичній площині і напрямлена в протилежний силі F бік, яка намагається зсунути тіло. Найбільша сила тертя має знаходиться на грані між спокоєм та рухом і дорівнює за модулем Ff = Fmax = /TV. Отже, на тіло з боку опорної поверхні діють дві реакції: нормальна N і дотична (сила тертя Ту). Додавши ці реакції за правилом паралелограма· дістанемо повну опорну реакцію R, яка утворює з нормальною реакцією TV деякий кут ц.

Найбільший кут ц, на який через тертя відхиляється від нормалі повна реакція R опорної поверхні, називається кутом тертя.

З рис. 6.6 маємо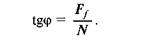

Але, як видно з формули (6.4),

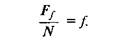
Отже,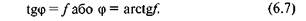

Тангенс кута тертя дорівнює коефіцієнту тертя ковзання. Інакше кажучи, кутом тертя називається кут, тангенс якого дорівнює коефіцієнту тертя ковзання.

Якщо тіло будемо переміщати відносно опорної поверхні в різні боки, то лінія дії реакції R опише конічну поверхню (рис. 6.6, б), яка називається конусом тертя. Отже, конусом тертя називають поверхню, яку описує повна реакція в разі з обертання навколо нормальної реакції. Якщо коефіцієнт тертя під час руху тіла в різних напрямках однаковий, то повна реакція поверхні відхиляється від нормальної в усіх напрямках на однаковий кут тертя φ і конус тертя буде круглим з кутом при вершині А, який дорівнює 2φ. Коли ж коефіцієнт тертя в різних напрямках різний (наприклад, у разі руху по дереву вздовж і поперек волокон), то конус тертя буде некруглим.

Для руху тіла необхідно, щоб рівнодіюча зовнішніх сил, що прикладені до нього, проходила за межами конуса тертя. Якщо ж рівнодіюча зовнішніх сил розташована всередині конуса тертя, то якою б вона великою не була, рух тіла неможливий, оскільки рушійна сила в цьому випадку завжди буде менша від сили тертя.

Нехай усі зовнішні сили, що діють на тіло, включаючи і його вагу, зводяться до однієї рівнодіючої сили 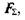яка проходить через точку А дотику тіла з поверхнею і утворює з нормаллю до поверхні кут б (рис. 6.6, <?). Перенесемо цю силу по лінії дії в точку А і розкладемо її на дві складові: 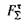, яка лежить у дотичній площині, і 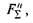направлену по нормалі до поверхні.

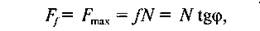Тоді згідно з формулами (6.4) і (6.1) максимальне значення сили тертя запишеться так:

 

де φ — кут тертя; N — модуль нормальної реакції, який, очевидно, дорівнює модулю нормального тиску 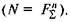Модуль сили 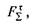яка намагається рухати тіло на поверхні, виразиться

формулою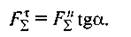

Для того щоб тіло залишалось на поверхні в рівновазі, необхідно витримати умови 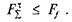Підставивши в цю умову

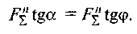значення 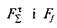, дістанемо

 

Звідси остаточно знайдемо умову рівноваги тілана площині:

Якщо збільшувати модуль сили 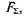залишаючи той же напрямок, то пропорційно збільшуватиметься не тільки модуль 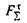рушійної сили, а й модуль сили тертя 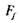, бо збільшується нормальний тиск 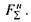Тіло стане рухатися лише тоді, коли рушійна

складова 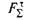рівнодіючої зовнішніх сил буде більшою від сили

тертя, а для цього необхідно так змінити напрямок сили 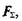щоб кут α був більшим від кута φ , тобто сила 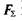проходила за межами конуса тертя (на рис. 6.6, в показано штриховою лінією). Отже, конус тертя визначає деяку область рівноваги спокою тіла під дією прикладених сил.

Тертя в поступальних кінематичних парах

За своєю конструкцією поступальні кінематичні пари бувають плоскі (рис. 6.7, а), клинові (рис. 6.7, 6) та циліндричні (рис. 6.7, в). У свою чергу, вони поділяються на горизонтальні та похилі.

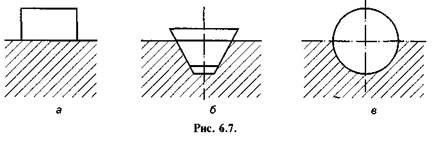
Основні закономірності тертя ковзання в плоских горизон­тальних поступальних кінематичних парах ми вже розглянули. Надалі розглядатимемо тертя ковзання в інших випадках.

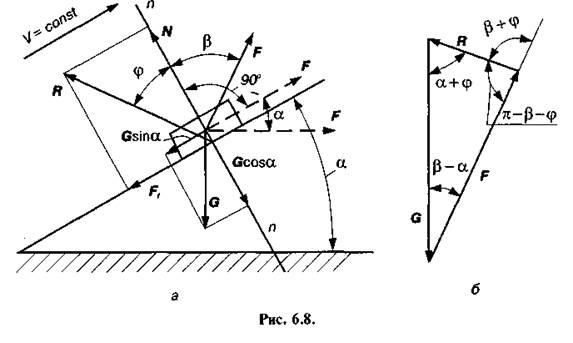
Тертя на похилій площині. Розглянемо загальний випадок рівномірного руху тіла вгору по похилій площині (рис. 6.8, а), яка утворює кут ос з горизонтом. Тіло вагою G приводиться в рух силою F, яка утворює з нормаллю з—з до похилої площини кут в.

При рівномірному русі тіла вгору по похилій площині на нього, крім сил F і G, діятиме нормальна реакція площини N і сила тертя Ff, яка напрямлена в протилежний від руху тіла бік. Замінимо сили N і Ff рівнодіючою R, що утворює з нормальною реакцією кут тертя ц (6.7).

Розглянемо умову рівноваги тіла під дією прикладених сил (F, G, R), на основі якої можна записати векторне рівняння

Тоді, побудувавши згідно з рівнянням (6.9) план сил (рис. 6.8, б), запишемо пропорцію

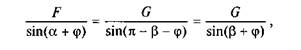
з якої знаходимо силу F, яка забезпечує рівномірний рух тіла по похилій площині та напрямлена під кутом в до нормалі з—з,

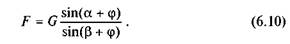
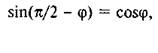Якщо сила F паралельна похилій площині 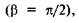то

 

 

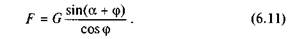
а значить,

 

 

Коли ж сила /"горизонтальна 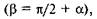то дістанемо

 

 

 
 

Остання формула широко використовується в інженерних розрахунках.

Якщо тіло рухається рівномірно вниз по похилій площині, то сила тертя Ff буде направлена в протилежний бік (вгору), а значить, повна реакція R — Ff+ N буде відхилена від нормалі п—п на кут (-ц). Тоді залежності (6.10)—(6.12) набувають вигляду

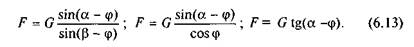
Характерно, що якщо кут нахилу площини менший від кута тертя (б < ц), то сила F (6.13) має знак мінус. Отже, у цьому разі для рівномірного руху тіла вниз по похилій площині треба замінити напрямок сили: сила F має "стягувати" тіло з похилої площини, бо інакше тіло перебуватиме в стані спокою. Площина, в якої кут нахилу б менший від кута тертя φ, називається самогальмівною.

Якщо б = φ , то сила F дорівнює нулеві. Це і є граничний випадок самогальмування.

Питання про рух повзуна по похилій площині з прискорен­ням можна вивчити на підставі аналогічних міркувань, коли до всіх діючих сил приєднати силу інерції тіла.

ККД похилої площини.Нехай тіло А під дією горизонтальної сили F переміститься вгору по похилій площині з положення І в положення II (рис. 6.9).

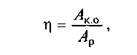ККД, як відомо, ви значається за формулою

де Ако — робота сил корисного опору; Ар — робота рушійних сил.

Якщо тіло рухається вгору по похилій площині, сила F напрямлена в бік руху і є рушійною силою, а значить, 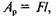сила G буде силою опору, а тому 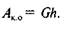Тоді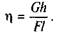

Враховуючи, що 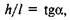де кут б — кут підйому похилої площини, а 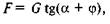дістанемо

Якщо тіло рухається вниз по похилій площині, сила G буде рушійною силою, a F — силою опору, а тому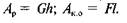

 
 

Тоді 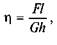або, взявши до уваги, щ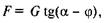о маємо

Із залежності (6.14)видно, що якщо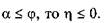

Похила площина, в якої 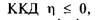є самогальмівною.

Самогальмування можливе і при русі тіла вгору по похилій площині. Для визначення кута нахилу самогальмування пло­щини необхідно покласти з = 0. З формули (6.13) випливає, щопри tga = 0 або Перший 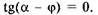розв'язок не

має 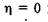змісту, оскільки при tga = 0 при a = 0, а значить, сила F ніякої корисної роботи не виконує (Gh = 0) — вона тільки долає силу тертя. Якщо

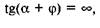то дістаємо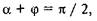

або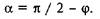

Таким чином, похила площина при підійманні тіла вгору самогальмівна, якщо кут підйому б дорівнює π / 2 - φ.

ККД є функція кута підйому площини з = з(б). З умови, що ККД дорівнює нулю при 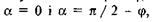треба припускати, що в проміжку між вказаними значеннями кута б ККД має найбільше значення.

Значення ат, при якому з максимальний, можна знайти відомим способом, дослідивши залежності (6.14) або (6.15) на ек­стремум. Якщо ці рівняння продиференціювати і прирівняти нулю: 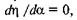то одержимо рівняння, з яких легко визначити ат.

При русі тіла вгору по похилій площині маємо

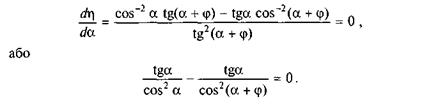
Замінивши тангенси відношенням sin і cos та привівши складові до спільного знаменника, після відповідних перетворень дістанемо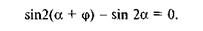

Це рівняння задовольняється тільки за умови, що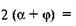

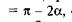оскільки 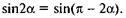Отже, максимальний ККД відповідає куту підйому

Якщо тіло рухається вниз по похилій площині, аналогічно дістаємо максимальне значення ККД при

Можна показати, що в разі піднімання повзуна по похилій площині, в якої кут підйому менший від кута ц, ККД завжди менший від 0,5. Справді, вже при α=φ рівняння (6.14) набуває такого вигляду:

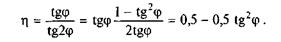
Отже, у цьому випадку з завжди менше від 0,5.

Виведені формули застосовуються для наближеного визначення ККД гвинтових та черв'ячних механізмів (передач). У разі передачі руху від черв'яка до колеса застосовується формула (6.14), а при передачі від колеса до черв'яка — формула (6.15). Усі наслідки, що випливають з цих формул для похилої площини, залишаються в силі для гвинтових і черв'ячних механізмів.

Тертя в клиновій поступальній парі.У деяких випадках по­верхня стикання повзуна і напрямної має в поперечному перерізі вигляд двогранного кута, або жолоба (рис. 6.10, а). Таку пару називають клиновою.

Нехай тіло 7, на яке діє вертикальна сила Q, під дією сили F рухається рівномірно вздовж горизонтальної напрямної 2. Повзун притискається до напрямної боковими поверхнями, на яких виникає сила тертя, що перешкоджає руху. Для того щоб тіло рухалось рівномірно в напрямній, повинна дотримуватися умова 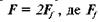— величина сили тертя, 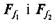що виникає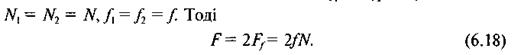

на кожній грані повзуна, причому 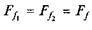, оскільки

Реакції нй, Н2 визначають з трикутника сил (рис. 6.10, б), якщо скористатися рівнянням Q + /V, + /V2 = 0. Враховуючи, що нй
 
 

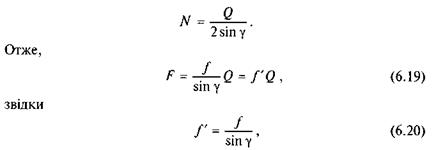= Н2 = Н, з

 

плану сил маємо

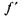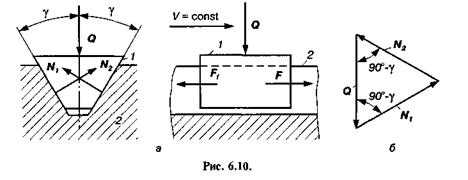
де — зведений (умовний) коефіцієнт тертя клинової пари. Оскільки завжди кут г менший 90°, то 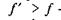— коефіцієнта

тертя плоскої поступальної пари. Цю властивість клинової пари широко використовують у техніці для збільшення сили тертя при передачі руху (наприклад, у пасових і фрикційних передачах, гвинтових з'єднаннях).

У всіх випадках, коли має місце тертя в клиновій парі, можна користуватися формулами для плоскої поступальної пари, в


які замість коефіцієнта тертя / і кута тертя ц підставляємо зве­дений коефіцієнт /' і зведений кут тертя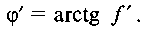

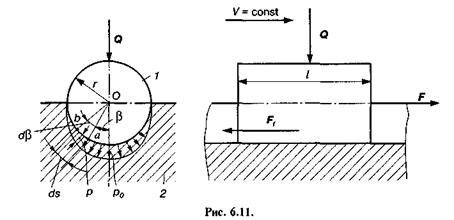
Циліндрична поступальна пара.Для визначення сили тертя Ff в такій парі (рис. 6.11) розглянемо елементарну частину ab = ds = = rdβ циліндричної поверхні циліндра / (повзуна). Тоді елементарна сила тертя для цієї частини визначається так: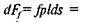

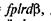
де с — питомий тиск на виділеному елементі напрямної; / — довжина повзуна; г — радіус циліндричної напрямної.

Повна величина сили тертя визначається за формулою

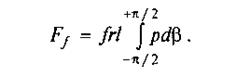
Досліди показують, що зміна тиску с підкоряється закону косинуса, тобто 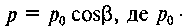— тиск (нормальна реакція) на

лінії дії сили Q. Тоді


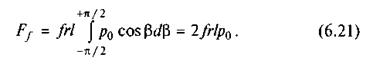
Зв'язок питомого тиску ра з величиною зовнішнього навантаження Q можна одержати, записавши рівняння проекцій на вертикаль:

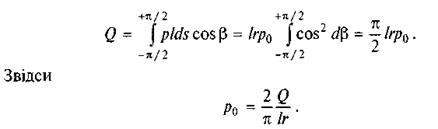
Підставляючи це значення у формулу (6.21), знаходимо силу тертя

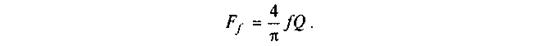
Позначивши 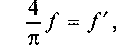зведений коефіцієнт тертя в

циліндричній поступальній парі, остаточно одержимо

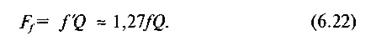
Із формули (6.22) видно, що сила тертя повзуна в циліндричній напрямній на 27 % більша від сили тертя в плоскій поступальній парі, але, враховуючи простоту виготовлення, циліндричні поступальні пари досить широко використовуються в техніці.

 

 
<== предыдущая лекция | следующая лекция ==>
ВИЗНАЧЕННЯ ЗВЕДЕНОГО МОМЕНТУ ІНЕРЦІЇ МЕХАНІЗМУ. | ТЕРТЯ У ГВИНТОВИХ КІНЕМАТИЧНИХ ПАРАХ

Дата добавления: 2016-06-15; просмотров: 5469;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.069 сек.