Интерполяционная формула Лагранжа

Пусть функция f(x) задана в (n + 1)узлах, произвольно расположенных на отрезке [a;b]:y₀ = f(x₀), y₁ = f(x₁), … y_n = f(x_n).

Требуется найти интерполирующий алгебраический многочленL_n(x), степени не выше n, удовлетворяющий условию (1.3.1-2), такой, что:

L₀ = y₀, L₁ = y₁, …, L_n = y_n. (1.3.2-1)

Будем искать L_n(x) вида:

L_n = Q₀(x)y₀ + Q₁(x)y₁ + … + Q_n(x) y_n, (1.3.2-2)

где Q_i(x) – коэффициенты, зависящие только от узлов , i=0,1,…,nи текущего значения х.

Для того чтобы выполнялись условия интерполяции (1.3.2-1), требуется, чтобы коэффициенты Q_i(x)удовлетворяли условию:

Действительно, чтобы L(х₀)=y₀, необходимо, чтобы в (1.3.2-2)

Q₀(x₀) = 1,Q₁(x₀) = 0, …, Q_n(x₀)=0.

В то же время в других узлах интерполяции первое слагаемое формулы 1.3.2-2, связанное с y_i, должно быть равно нулю, то есть:Q₀(x_i) =0,i = 1, 2, … , n.

Этим требованиям отвечает коэффициент вида:

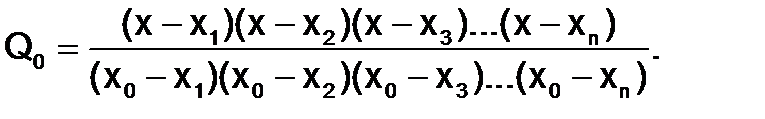(1.3.2-3)

Поскольку в числителе Q₀(x) записано произведение разностей со всеми узлами кроме х₀, то Q₀(x) обращается в ноль при х = х_i ; i = 1, 2, … , n. В то же время при х = х₀числитель и знаменатель дроби взаимно сокращаются и Q₀(x₀)=1.

Для того чтобы L_n(x₁) = y₁, коэффициенты в (1.3.2-2) должны принять значения:

Q₁(x₁) = 1; Q₀(x₁) = 0…Q_n(x₁) =0.

Чтобы в других узлах коэффициент Q₁(x), связанный с y_i, принял значение ноль,нужно, чтобы Q₁(x_i) = 0, i = 0, 2, 3, …, n. Тогда произведение разностей в числителе обращается в ноль во всех узлах, кроме х₁, а при х = х₁коэффициент равен 1.

Обобщая сказанное выше, получим выражение для Q_i(x):

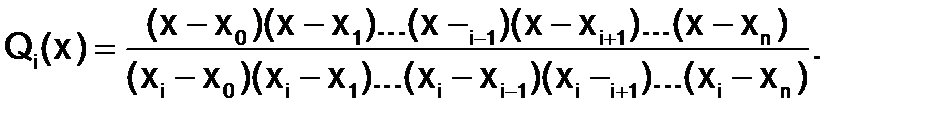(1.3.2-4)

Для интерполяционного многочлена Лагранжа это выражение будет следующее:

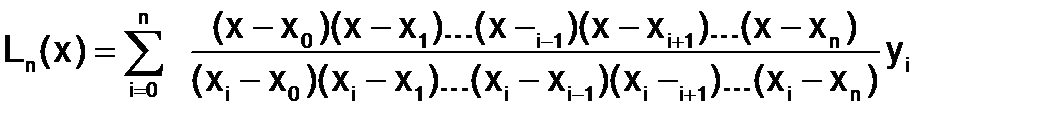. (1.3.2-5)

Несмотря на громоздкость (1.3.2-5), одним из преимуществ формулы Лагранжа является возможность ее записи непосредственно по заданной таблице значений функции. Для этого следует учесть следующее правило: формула содержит столько слагаемых, сколько узлов в таблице; каждое слагаемое – это произведение дробного коэффициента на соответствующее значение y_i; числитель коэффициента при y_i содержит произведение разностей х со всеми узлами кроме 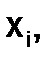а знаменатель полностью повторяет числитель при х= .

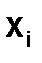Используя приведенные правила, получим формулы Лагранжа для двух узлов (n=1) - линейная интерполяция:

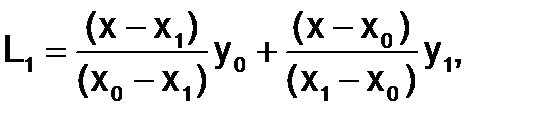
для трех узлов (n=2) - квадратичная интерполяция:

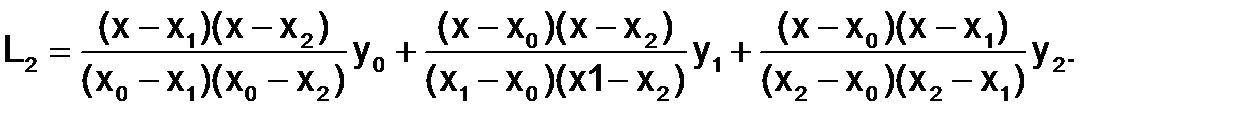(1.3.2-6)

Оценку погрешности формулы Лагранжа определяют исходя из приближенного равенства

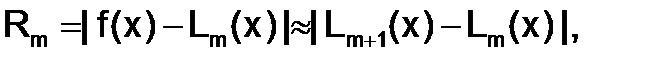
где m– число узлов, используемое в формуле.

Для того, чтобы уменьшить погрешность интерполяции, используется прием перенумерации узлов исходной таблицы, последовательно выбирая в качестве х₀, 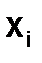, х₂ и т.д. узлы, наиболее близко расположенные к искомой точке х, по возможности симметрично относительно точки х₀. Такой прием позволяет уменьшить степень интерполяционного полинома для достижения требуемой точности (не использовать все заданные узлы).

Схемы алгоритма интерполяции с помощью формул Лагранжа приведены на
рис. 1.3.2-1 и1.3.2-2.

Рис. 1.3.2-1. Схема алгоритма интерполяции по формуле Лагранжа

Рис. 1.3.2-2. Схема алгоритма процедуры-функции LX() вычисления многочлена

Лагранжа к-ой степени в точке xl

Пример 1.3.2-1.Пусть функцияy = f(x) задана таблично:

Требуется с использованием формулы Лагранжа вычислить значение f(x) в точке x = 1.45.

Перенумеруем узлы:

x₀ = 1.4 y₀ =-0.24

x₁ = 1.6 y₁ = -0.24

x₂ = 1.2 y₂ = -0.16

х₃ = 1.8 y₃ = -0.16

x₄ = 1.0 y₄ = 0.0 .

Для приближенного вычисления значения функции воспользуемся формулами линейной и квадратичной интерполяции:

При n + 1 = 2 используем узлы x₀ и x₁

.

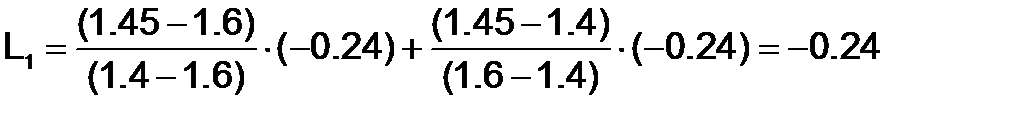При n +1 = 3используем узлы x₀ , x₁ иx₂

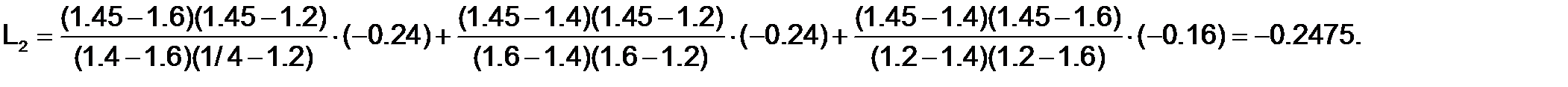
Для оценки погрешности используем соотношение

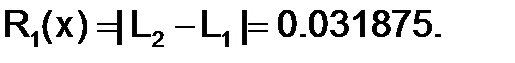
Если полученная величина соответствует заданной погрешности (например,e=0.1), то вычисления прекращают. Если e<R_n, то количество узлов увеличивают.Вычисления повторяют до тех пор, пока не выполнится условие R_n≤e.

Если, в соответствии с условиями поставленной задачи, требуется найти значения функции не в одной, а в нескольких точках, то рекомендуется провести преобразования формулы и получить многочлен в явном виде (Пример 1.3.1-1).

Если в формуле были использованы все точки, заданные таблицей, то оценить погрешность не представляется возможным.