Примеры составления программ

Пример 4.2.1. Программа решения уравнений методом деления отрезка пополам.

Задание: решить уравнение ex - 10x = 0.

PROGRAM del;

USES Crt;

LABEL 1,2;

VAR a, b, x0, eps, r1, r2: Real;

{ a, b - Начало и конец интервала }

{ x0 - Корень уравнения }

{ eps - Точность расчета }

k: Integer;

fin, fout: Text;

FUNCTION f(x:real): Real; { Исследуемая функция }

BEGIN

f:=exp(x)-(10*x);

END;

BEGIN

ClrScr; { Очистка текстового экрана }

assign(fin,'otrezok.in'); { Файл данных }

assign(fout,'otrezok.out'); { Файл вывода }

reset(fin);

read(fin,a,b,eps);

close(fin);

(* Р А С Ч Е Т *)

k:=0; 1:k:=k+1;

x0:=(a+b)/2;

IF f(x0)=0 THEN GOTO 2;

IF abs(b-a)<eps THEN GOTO 2;

r1:=f(x0);

r2:=f(a);

IF (r1*r2)<0 THEN b:=x0

ELSE a:=x0;

GOTO 1;

2: writeln('Число делений пополам: ',k);

writeln('Корень уравнения: ',x0:7:4);

writeln('Точность расчета: ',eps:7:6);

(* Запись в файл *)

rewrite(fout);

writeln(fout,'Число делений пополам: ',k);

writeln(fout,'Корень уравнения: ',x0:7:4);

writeln(fout,'Точность расчета: ',eps:7:6);

close(fout);

readln;

END.

ФАЙЛ исходных данных:

0.0 1.0 1.0E-08 a, b - Начало и конец интервала eps - Точность расчета

ФАЙЛ с результатами

Число делений пополам: 28

Корень уравнения: 0.1118

Точность расчета: 0.000000001

Пример 4.2.2. Программа решения уравнения с использованием метода Ньютона.

Уравнение x3- 2x2 + 1.3x = 0.

PROGRAM newton;

LABEL m1, m2;

VAR x, x0, eps:real;

a1, a2:text;

k:integer;

FUNCTION f(x0:real):real;

BEGIN

f:=x*x*x-2*x*x+1.3*x-0.2;

END;

FUNCTION f1(x0:real):real;

BEGIN

f1:=3*x*x-4*x+1.3;

END;

BEGIN

assign (a1,'dat17-2');

reset(a1);

read(a1,x0,eps);

k:=0;

m2: x:=x0;

x0:=x-f(x)/f1(x);

k:=k+1;

IF abs(x-x0) <= eps THEN GOTO m1

ELSE GOTO m2;

m1: assign(a2,'res-17-2');

rewrite(a2);

writeln(a2,'корень уравнения',x,k);

close (a2);

END.

Пример 4.2.3. Программа решения уравнения методом итераций.

PROGRAM met;

LABEL m1, m2;

VAR x, x0, eps:real;

a1, a2:text;

k:integer;

FUNCTION f(x0:real):real;

BEGIN

f:=(-x0*x0*x0+2*x0*x0+0.24)/1.3;

END;

FUNCTION f1(x0:real):real;

BEGIN

f1:=-3*x0*x0+4*x0+1.3;

END;

BEGIN

assign (a1,'dat-21'); reset(a1);

read(a1,x0,eps);

k:=0;

REPEAT

x:=x0;

writeln (x0);

x0:=f(x); k:=k+1;

UNTIL abs(x-x0) < eps ;

m1: assign(a2,'res-21'); rewrite(a2);

writeln(a2,'корень уравнения',x,k);

close (a2);

END.

4.3. Приближенное решение обыкновенных дифференциальных уравнений первого порядка

При решении научных и инженерно-технических задач часто бывает необходимо математически описать какую-либо динамическую систему. Лучше всего это делать в виде дифференциальных уравнений (ДУ) или системы дифференциальных уравнений. Наиболее часто такая задача возникает при решении проблем, связанных с моделированием кинетики химических реакций и различных явлений переноса (тепла, массы, импульса) – теплообмена, перемешивания, сушки, адсорбции, при описании движения макро- и микрочастиц.

Обыкновенным дифференциальным уравнением (ОДУ) n-го порядка называется следующее уравнение, которое содержит одну или несколько производных от искомой функции y(x):

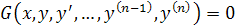
где обозначает производную порядка n некоторой функции y(x), x – это независимая переменная.

Решением обыкновенного дифференциального уравнения называется такая функция y(x), которая при любых х удовлетворяет этому уравнению в определенном конечном или бесконечном интервале. Процесс решения дифференциального уравнения называют интегрированием дифференциального уравнения.

Общее решение ОДУ n-го порядка содержит n произвольных констант C1, C2, …, Cn

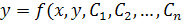
Частное решение ОДУ получается из общего, если константам интегрирования придать некоторые значения, определив некоторые дополнительные условия, количество которых позволяет вычислить все неопределенные константы интегрирования.

Точное (аналитическое) решение (общее или частное) дифференциального уравнения подразумевает получение искомого решения (функции y(x)) в виде выражения от элементарных функций.

Численное решение ДУ (частное) заключается в вычислении функции y(x) и ее производных в некоторых заданных точках x₁,x₂,…,x_N,лежащих на определенном отрезке.

Метод Эйлера

Простейшим численным методом решения обыкновенных дифференциальных уравнений является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки:

,

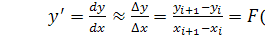где y_i+1 – это искомое значение функции в точке x_i+1.

Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить y_i+1, если известно y_i в точке х_i:

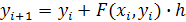
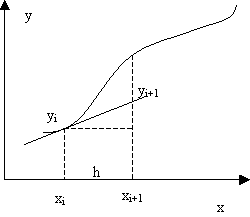
Рис.4.1. Графическая иллюстрация метода Эйлера

Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=xi. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:

Пример 4.3.1 Рассчитать кинетику гомогенной химической реакции, используя метод Эйлера.

VAR ca0, cb0, cc0, cd0, k1, k2, k3, k4, t0, tk, h, ca, cb, cc, cd: Real;

{Описание переменных концентрации, констант скорости, время реагирования, шага}

f1, f2 :Text;

{Файловые переменные}

BEGIN

assign(f1,'al_ar.in');

{Файл ввода данных}

assign(f2,'al_ar.out');

{Файл вывода расчетов}

reset(f1);

readln(f1,ca0,cb0,cc0,cd0,k1,k2,k3,k4,t0,tk,h);

{ Ca0, Cb0, Cc0, Cd0 - Концентрации веществ для t0 }

{ k1, k2, k3, k4 - Константы скорости для каждой реакции }

{ t0, tk - Начальное и конечное время реагирования }

{ Ca, Cb, Cc, Cd - Переменные для расчета концентраций }

close(f1);

ca:=ca0; cb:=cb0; cc:=cc0; cd:=cd0;

rewrite(f2);

writeln(f2,'Метод Эйлера');

writeln(f2,'Время Концентрация');

writeln(f2,' А B С D ');

REPEAT

ca:=ca0+h*((-1*(k1+k4))*ca0+k3*cd0);

cb:=cb0+h*(k1*ca0-k2*cb0);

cc:=cc0+h*k2*cb0;

cd:=cd0+h*((k4*ca0)-(k3*cb0));

writeln(f2,' ',t0:8:4,' ',ca:8:4,' ',cb:8:4,' ',cc:8:4,' ',cd:8:4,' ');

ca0:=ca; cb0:=cb; cc0:=cc; cd0:=cd; t0:=t0+h;

UNTIL t0>=tk;

writeln(f2,' ',t0:8:4,' ',ca:8:4,' ',cb:8:4,' ',cc:8:4,' ',cd:8:4,' ');

close(f2);

END.

Метод Рунге-Кутта

Дальнейшее улучшение точности решения ОДУ первого порядка возможно за счет увеличения точности приближенного вычисления интеграла в выражении.

Воспользовавшись формулой Симпсона, можно получить еще более точную формулу для решения ОДУ первого порядка – широко используемого в вычислительной практике метода Рунге-Кутта.

В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [x_i+1 x_i].

,

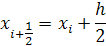тогда можно переписать так:

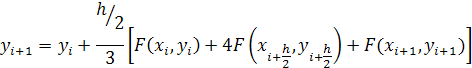
Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции y_i+h/2 и y_i+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений

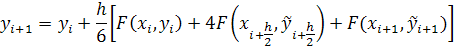
При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутта различного порядка точности.

Алгоритм Рунге-Кутта третьего порядка (погрешность порядка h³):

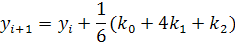
где

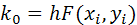
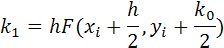
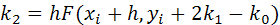
Алгоритм Рунге-Кутта четвертого порядка (погрешность порядка h⁴):

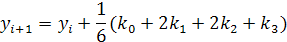
где

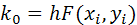
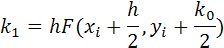
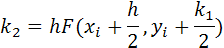
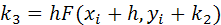
Пример 4.3.2 Рассчитать кинетику гомогенной химической реакции, используя метод Рунге-Кутта.

VARca, cb, cc, cd, ca0, cb0, cc0, cd0, k1, k2, k3, k4, t0, tk, h:real;

{Ca, Cb, Cc, Cd - Концентрации веществ до реакции }

{k1, k2, k3, k4 - Скорости для каждой из реакций}

{t0, tk - Начальное и конечное время реагирования}

{h - шаг}

x, q1, q2, q3, q4, q5, q6, q7, q8, q9, q10, q11, q12, q13, q14, q15, q16:real;

{Qn - Коэффициенты Рунге-Кутты}

f1, f2:text;

BEGIN

assign(f1,'runge.in');{Файл с данными}

assign(f2,'runge.out'); {Файл с результатами }

reset(f1); read(f1,ca0,cb0,cc0,cd0,k1,k2,k3,k4,t0,tk,h);

close(f1);

cc:=cc0;ca:=ca0;cb:=cb0;cd:=cd0; x:=t0;

rewrite(f2);

Writeln(f2,' Метод Рунге - Кутта');

writeln(f2,' Время Концентрация ');

writeln(f2,'A B С D ');

REPEAT

q1:=h*((-1)*(k1+k4)*ca0+(k3*cd0));

q2:=h*((-1)*(k1+k4)*(ca0+q1/2)+(k3*(cd0+q1/2)));

q3:=h*((-1)*(k1+k4)*(ca0+q2/2)+(k3*(cd0+q2/2)));

q4:=h*((-1)*(k1+k4)*(ca0+q3)+(k3*(cd0+q3)));

q5:=h*((k1*ca0)-(k2*cb0));

q6:=h*((k1*(ca0+q5/2))-k2*(cb0+q5/2)));

q7:=h*((k1*(ca0+q6/2))-(k2*(cb0+q6/2)));

q8:=h*((k1*(ca0+q7))-(k2*(cb0+q7)));

q9:=h*(k2*cb0);

q10:=h*(k2*(cb0+q9/2));

q11:=h*(k2*(cb0+q10/2));

q12:=h*(k2*(cb0+q10));

q13:=h*((k4*ca0)-(k3*cb0));

q14:=h*((k4*(ca0+q13/2))-(k3*(cb0+q13/2)));

q15:=h*((k4*(ca0+q14/2))-(k3*(cb0+q14/2)));

q16:=h*((k4*(ca0+q15))-(k3*(cb0+q15)));

ca:=ca0+((q1+q2+q3+q4)/6);

cb:=cb0+((q5+q6+q7+q8)/6);

cc:=cc0+((q9+q10+q11+q12)/6);

cd:=cd0+((q13+q14+q15+q16)/6);

writeln(f2,' ',x:8:4,' ',ca:8:4,' ',cb:8:4,' ',cc:8:4,' ',cd:8:4,' ');

ca0:=ca; cb0:=cb; cc0:=cc; cd0:=cd;

x:=x+h;

UNTIL x>=tk;

writeln(f2,' ',x:8:4,' ',ca:8:4,' ',cb:8:4,' ',cc:8:4,' ',cd:8:4,' ');

close(f2);

END.