Механическое истолкование производной

Мгновенная скорость в механике определяется как предел отношения приращения перемещения к приращению времени 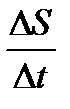при Dt ® 0, т.е. v = S¢(t)

Таким образом, производная перемещения по времени в механике характеризует скорость движения тела. Это есть механическое истолкование производной.

Уравнение касательной

Производная линейной функции y = kx + b равна угловому коэффициенту k. Производная функции y = f(x) в любой точке равна угловому коэффициенту касательной функции в этой точке, т.е. производная характеризует скорость изменения функции. Это есть геометрическое истолкование производной (рис. 3.1).

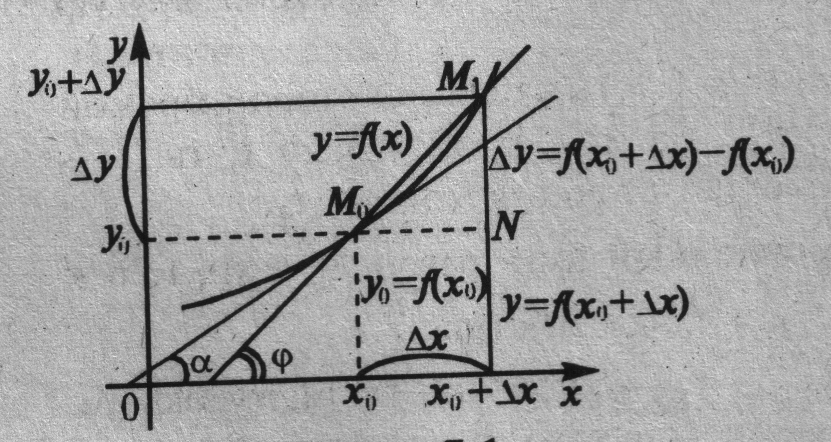
Рис. 3.1. Геометрическое истолкование производной

Производная применяется для нахождения уравнения y(x) касательной функции f(x) в заданной точке x = x₀ :

y = f¢(x₀)x + b, f(x₀) = f¢(x₀)x₀ + b, b = – f¢(x₀)x₀ + f(x₀).

В итоге получается уравнение y(x) касательной функции f(x) в заданной точке x = x₀ :

y = f(x₀) + f¢(x₀)(x – x₀).

@ Задача 3. Найти уравнение касательной функции f(x) = x² в точке x₀ = – 1.

Решение: Находим f(x₀) = (– 1) ² = 1, потом f¢(x) = 2x и

f¢(–1) = 2(– 1) = –2, после чего y = 1 – 2(x + 1) = – 2x – 1.

Предельный анализ

Предельный анализ – это раздел экономики, где используется дифференциальное исчисление. Основные понятия предельного анализа, это предельный доход, предельные издержки, предельная производительность и т.д.

Предельный доход R¢(Q) – это изменение суммарного дохода при изменении объема реализации на единицу.

Предельные издержки C¢(Q) – это изменение полных издержек, при изменении объема продукции на единицу.

Предельная склонность к потреблению C¢(Y) – это производная потребления по национальному доходу.