Область определения функции
Математический анализ и дифференциальные уравнения
Функции
Функция
Величина y называется функцией переменной величины x, если каждому из возможных значений x, соответствует одно или несколько определенных значений y.
þ Обозначение: y = f(x) («игрек равно эф от x»)
При этом переменная x называется аргументом (независимым переменным), а у - функцией (зависимым переменным).
! Примеры: Функциями являются зависимости температуры, скорости движения и высоты брошенного вверх тела от времени.
Если каждому значению аргумента отвечает одно значение функции, то функция называется однозначной; если два или больше значений, то - многозначной.
! Примеры: В каждый момент времени сутки температура в данной местности принимает одно единственное значение (однозначная функция); каждой высоте, на которой брошенное вверх тело может находится, соответствуют два определенных значений времени (одно при поднятии, другое при спуске) (двузначная функция).
Область определения функции
Множество всех значений X (xÎX), которые может принимать аргумент функции x, называется областью определения этой функции.
Множество всех значений Y (yÎY), которые может принимать функция f(x), называется областью значений этой функции.
! Примеры: Областью определения функции y = x² является интервал (– ¥; ¥), а областью значений функции – интервал [0; ¥).
@ Задача 1. Найти область определения функции 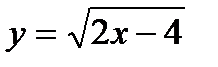 .
.
Решение: Область определения функции находится как решение неравенства 2x – 4 ³ 0 Þ x ³ 2, т.е. x Î [2; ¥).
@ Задача 2. Найти область определения функции 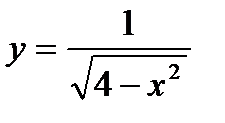 .
.
Решение: Область определения функции находится как решение неравенства 4 – x² > 0 Þ – 2 < x < 2, т.е. x Î (–2; 2).
Дата добавления: 2016-06-15; просмотров: 2125;











