Производная функции
Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a, b), и пусть x – какая-то точка этого промежутка. Дадим аргументу приращение Dx, тогда функция получит приращение, равное Dy = f(x + Dx) – f(x). Если функция непрерывная и приращение аргумента бесконечно малая величина, то приращение функции тоже бесконечно малая величина.
Предел, к которому стремится отношение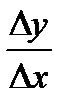 
при Dx® 0, называется производной функции:
.
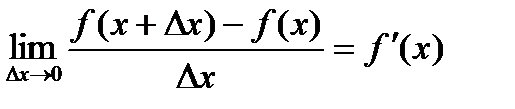þ Обозначение: f¢(x) («эф штрих икс»), y¢ («игрек штрих»)
! Примеры производных линейной функции y = x и квадратичной функции y = x2.
.
.
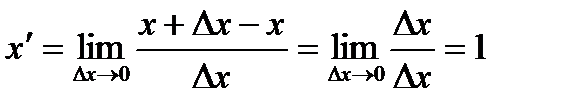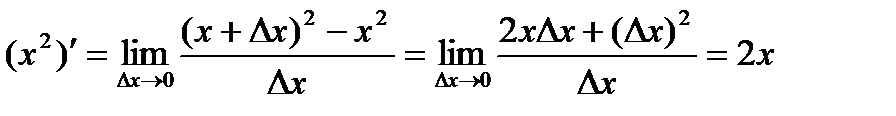Производная степенной функции равна произведению степени на степенную функцию, у которой показатель на единицу меньше:
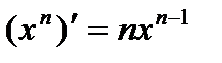. (1)
Производные функций y = x, y = x2 являются частными случаями формулы (1), при n = 1; 2. Производные 1¢ = 0,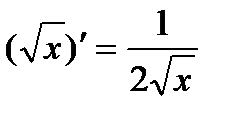 
, 
, 
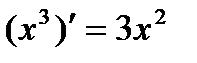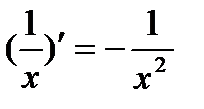тоже являются частными случаями формулы (1), при n = 0; ½; 3; – 1.
! Пример: Производная тригонометрической функции y = sinx равна
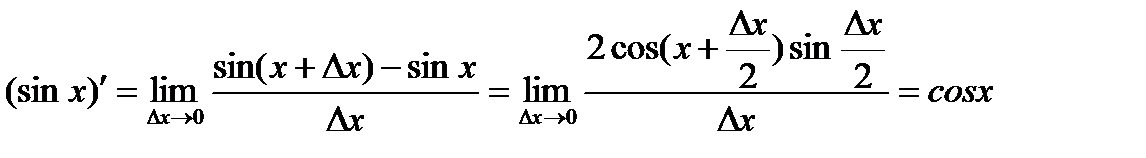. (2)
Таким же образом находится производная функции cosx:
(cosx)¢ = – sinx. (3)
! Пример: Производная экспоненциальной функции y = ex равна
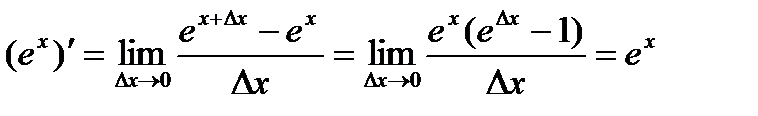. (4)
Дата добавления: 2016-06-15; просмотров: 1716;
Поиск по сайту
Узнать еще
- I. Общие принципы структурно-функциональной организации клетки и её компоненты. Плазмолемма, её структура и функции.
- II. Митохондрии (строение и функции)
- II. Признаки, ресурсы и функции власти.
- III. Функции отдела по делам ГОЧС и ВМР
- III. Функции политологии. Возрастание роли политических знаний в жизни общества.
- Table 1. Функции ГИС для лесного хозяйства и лесоустройства
- А.Н.Леонтьев ПВ – это профессиональное общение педагога, имеющее определенные функции, направленное на оптимизацию учебной деятельности
- Абсолютная и относительная погрешности функции
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
