Дослідження руху механізмів методом Віттенбауера

Цей метод випливає з відомої залежності кінетичної енергії механізму.

У цій формулі J_зв ^_ зведений момент інерції, а w - кутова швидкість ланки зведення механізму (машини). Залежність (4.55) можна записати так:

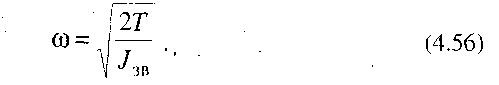
Таким чином, кутову швидкість ланки зведення у кожному поло­женні механізму можна визначити, знаючи відношення його кінетичної енергії до зведеного моменту інерції, взятих для цього ж положення. Інак­ше кажучи, треба мати залежність T = T(J_ЗВ), яка встановлює зв'язок між кінетичною енергією Т і зведеним моментом інерції J_зв. Цю задачу зруч­но розв'язувати графічно. Спочатку будують діаграми кінетичною енергії Т =T( 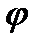) і зведеного моменту інерції J_зв =J_зв 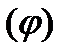залежно від кута пово­роту ланки зведення, потім, на основі цих діаграм, будують діаграму T = T(J_ЗВ), виключивши спільний параметр 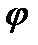. Якщо побудова діаграми J_зв = J_зв( 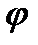) не складає труднощів (це питання ми розглянули вище п.4.7). то для побудови діаграми Т = T( 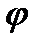) необхідно мати діаграми зведених мо­ментів рушійних сил М_р =М_р ( 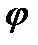) і сил опору М₀ =М₀( 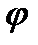). Такі діаграми

будують на основі механічних характеристик двигунів і робочих машин. Практично це досить складні задачі, які, як правило, розв'язуються з пев­ними припущеннями.

Нехай задано діаграми зведених моментів рушійних сил М_р = М_р( 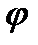) і сил опору М₀ = М₀(ф) у функції кута повороту початкової ланки (рис. 4.17, а) [1]. Маючи такі діаграми, можна знайти роботи рушій­них сил і сил опору на вибраному інтервалі за допомогою наступних фор­мул:

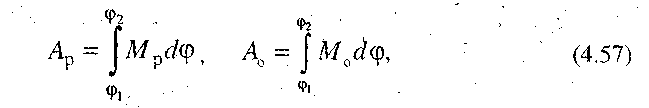
де кут 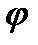- кут повороту ланки зведення. Величина цих робіт виражається у масштабі площею, що обмежена відповідною кривою М_р=М_р ( 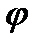) чи М₀ = М₀( 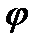), віссю ф і крайніми ординатами вибраного інтервалу ,

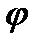Приріст кінетичної енергії механізму за будь-який проміжок часу, що виражається рівнянням

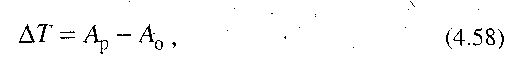
дорівнює різниці площі кривих М_р=М_р ( 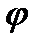) і М₀ =М₀( 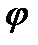), помноженій на відповідні масштаби моментів 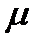_м і кута повороту .

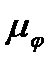Отже, зміна кінетичної енергії завжди пропорційна площі, яка знаходиться між кривими моментів рушійних сил і сил опору (на рис. 4.17,а ці площі заштриховані). Цим площам треба приписувати знак „+" або „-" залежно від того, яка робота буде більша: моменту рушійних сил чи моменту сил опору. Підрахувавши величину площі вказаних вище площадок, можна побудувати діаграму T=T( 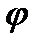) зміни кінетичної енергії ланки зведення у функції кута повороту 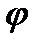(рис. 4.17,6). Побудову почнемо з першого ін­тервалу 1-2. Обчислюємо площу (1 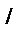2'2"1") у квадратних міліметрах. Нехай ця площа дорівнює S₁₂ , мм², тоді приріст кінетичної енергії на цьому ін­тервалі буде

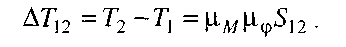
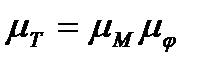Оскільки механізм почав рухатися з положення, що відповідає точці 1, то, очевидно, що початковий запас кінетичної енергії Т₁ дорівнює нулю і повний запас кінетичної енергії механізму в положенні 2 виразиться вели­чиною Т₂ = T₁₂. Цю величину відкладаємо у вигляді відрізка 2-2' у масш­табі на ординаті, проведеній у точці 2 (рис. 4.17, б). Маємо

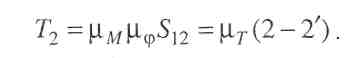
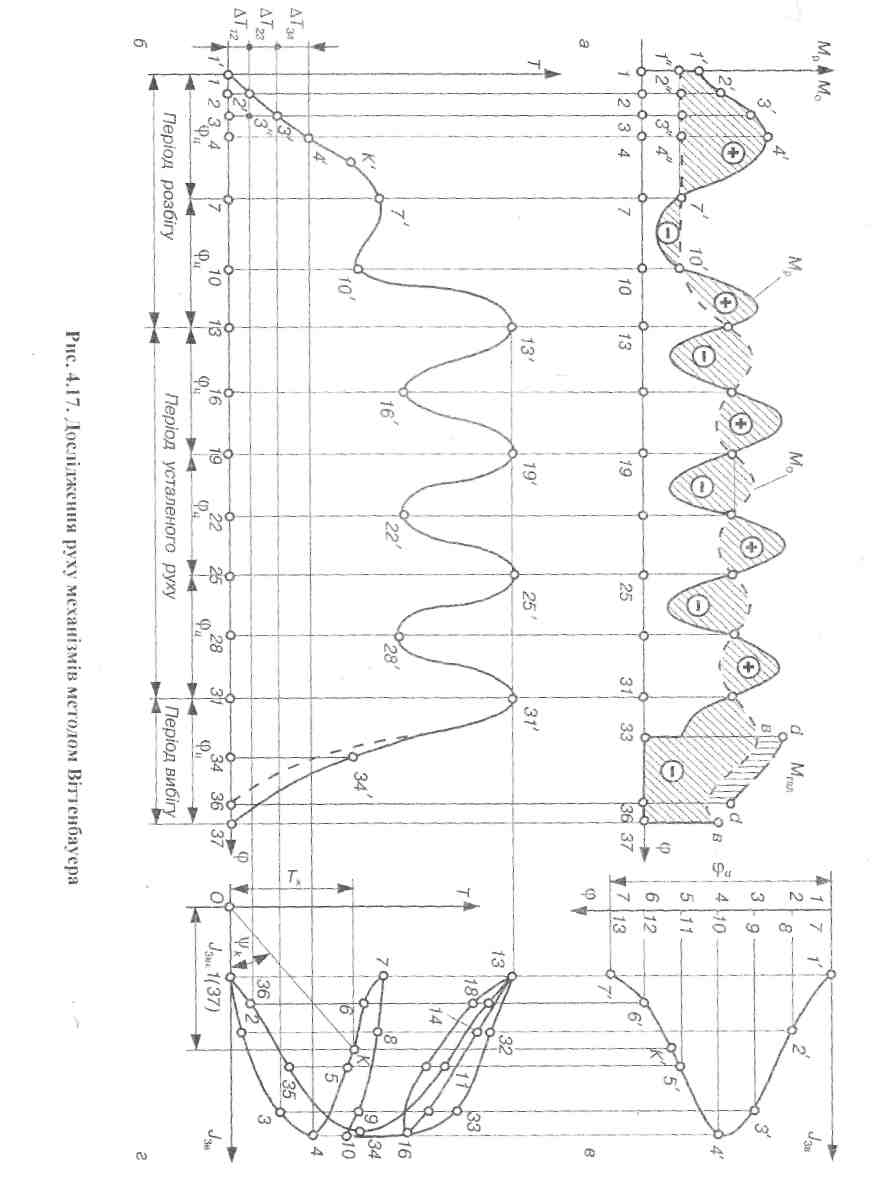
Далі обчислюємо наступну площу S₂₃ = (2"2'3'3"), мм². На підставі попе­реднього маємо Т₂₃ =Т₃—Т₂ = 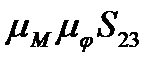= 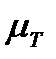(3-3), тобто приріст кіне­тичної енергії на ділянці 2-3 виражається площею (2"2'3'3") мм , помноженою на добуток масштабів \і_м і ц_ф . Знайдену величину T₂₃ відкладаємо на ординаті в точці 3 у вигляді відрізка З"-З' у масштабі 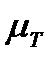, додаючи його до попереднього відрізка - (3-3')=(2-2')+(3"-3') і т.п. Ординати діаграми кінетичної енергії збіль­шуються до положення 7, де в точці 7' вона має вершину, що відповідає одному з максимумів кінетичної енергії. Далі на ділянці 7-10 крива опускається, оскільки заштрихована площа, що міститься між цими точками осі абсцис, має знак "-" (М₀ > М_р). Починаючи з точки 10, крива кінетичної енергії підіймається до по­ложення 13, де ця крива знов має вершину у точці 13' і т.п. На ділянці 13-31, де діаграма описує усталений рух, крива повторюється через кожний цикл руху механізму, що відповідає куту 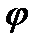_ц, причому ордината її досягає то свого макси­муму, то свого мінімуму. У положенні 31 ордината кривої Т = T( 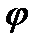) має останній максимум, після чого спадає завдяки наявності на ділянці 33-37 тільки сил опору, а на ділянці 31-33 М₀ > М_р . Точка 37 відповідає моменту зупинки механізму, тобто повному вичерпанню кінетичної енергій нагромадженої в період розгону. Очевидно, що витрати цієї енергії можна прискорити, ввівши додаткові опори (га­льма). На рис. 4.17, а, б гальмівний момент М_гал і кінетична енергія Т відповідно зображені штриховими лініями.

Отже, за весь час роботи механізму від точки 1 до точки 37 приріст кіне­тичної енергії дорівнює нулю, тобто сума всіх заштрихованих площадок із знаком „+" повинна дорівнювати сумі площадок із знаком „-", оскільки в момент пуску механізму і в момент його зупинки швидкість ланки зведення дорівнює нулю Така сама рівність повинна мати місце і за час усталеного руху (13-31), оскільки у цьому випадку швидкість ланки зведення механізму через кожний цикл повер­тається до попереднього значення. На рис. 4.17, а умовно показано три повних цикли 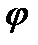_ц усталеного руху. Практично число цих циклів може бути різним зале­жно від часу безперервної роботи машини.

Діаграму зведених моментів інерції досить побудувати тільки для одного циклу 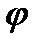_ц роботи механізму (рис. 4.17, в), оскільки J_зв є функцією положень механізму 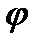(див. п. 4.7). Для зручності наступної побудови кривої Віттенбауера діаграму J_ЗВ=J_ЗВ( 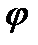) повернуто на 90°.

Маючи діаграми T= Т( 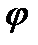) і J_Зв ⁼ Jзв( 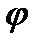),будуємо діаграму T = T(J_ЗВ) (рис. 4.17,г), для цього на осі ординат відкладаємо значення кі­нетичної енергії, що визначаються відрізками 1-1, 2-2', 3-3' і т.д. діаграми Т =T( 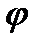), а по осі абсцис - значення зведеного моменту інерції, що визна­чається відрізками 1-Г, 2-2', 3-3' і т.д. діаграми J_ЗВ=J_ЗВ( 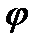).Знайдені точки 1, 2, 3 і т. п. у системі координат Т - J_зв послідовно з'єднуємо плав­ною кривою, дістаємо криву кінетичної енергії Т у функції зведеного момен­ту інерції, тобто залежність Т = T(J_ЗВ) . Цю криву називають кривою Віт­тенбауера за ім'ям австрійського вченого, який вперше розглянув цей метод.

За допомогою кривої Віттенбауера легко встановити залежність куто­вої швидкості ланки зведення у функції кута повороту ер. Для цього вибере­мо на кривій Т = T(J_зв) будь-яку точку К і з'єднаємо цю точку з точкою 0 - початком координат (рис. 4,17, г). Позначимо кут, утворений прямою 0K з віссю абсцис, через 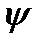_к, Оскільки по осі абсцис відкладено зведений мо­мент інерції I_звК у масштабі 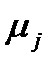, а по осі ординат - кінетичну енергію Т_к у масштабі 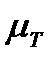які відповідають точці К, то очевидно, що відношення цих ве­личин дасть тангенс кута 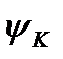нахилу кривої ОК до осі J_зв , тобто:

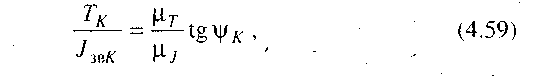
де J_зв=0К₁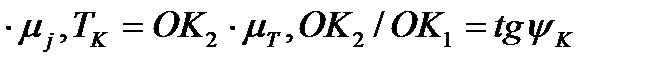

Тоді швидкість ланки зведення в положенні, яке визначається точ­кою К, знаходимо за формулою (4.56), тобто

Аналогічно визначають швидкості ланки зведення в інших поло­женнях механізму. Використовуючи ці значення, можна побудувати графік кутової швидкості w ланки зведення у функції кута 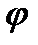(див. рис. 4.14),тобто графік w= w( ).

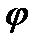Графік часу t руху у функції кута може бути побудований, якщо використати умову w =d 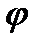/dt, оскільки будь-який проміжок часу від початку руху до даного моменту часу t_і дорівнює:

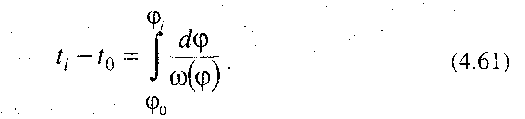
Інтеграл у правій частині формули (4.61) можна визначити графіч­но, якщо побудувати графік величини w( 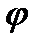) у функції кута 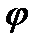, оскільки відома функція w=w( 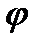). За графіками w = w( 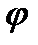) і t= t( 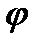) можна побуду­вати графік w=w( 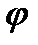). Кутове прискорення є ланки зведення визначається графічним диференціюванням функції w= w(t).

Знаючи кутову швидкість w і кутове прискорення 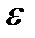ланки зведен­ня, можна визначити швидкості, прискорення і сили інерції окремих ланок, а також виконати силовий розрахунок механізму в умовах нерівномірного обертового руху ланки зведення.

Таким чином, за допомогою кривої Віттенбауера можна повністю дослідити рух машинного агрегата при силах, що залежать від положення ланки зведення.

Питання для самоперевірки

1. Основні задачі динамічного дослідження механізмів. 2. Поняття про силу. Які сипи відно­сяться до рушійних, сі які до корисного і шкідливого опору⁹ 3. Запишіть формули дія визначення роботи і потужності сили (моменту). 4. Що розуміють під механічною характеристикою машини ⁹ 5. Як визна­чити величину й напрямок сичи (моменту) інерції? 6. Які задачі силового розрахунку механізмів і його практичне значення? 7. З якою метою в систему діючих сил вводять сипи (моменти) сип інерції? Прин­цип Даламбера. 8. Яку систему називають статично визначеною? Яка система є статично визначеною в механізмах? 9. Яка послідовність силового розрахунку механізмів? 10. Що наперед відомо про напря­мок, величину і точку прикладання реакцій в поступальній, обертовій парах V класу та вищій парі IVкла­су (без врахування сил тертя). 11. Методика силового розрахунку структурних груп і механізму І класу. Поняття про зрівноважувальну сипу (момент). Яким способом можна визначити зрівноважувальну си­лу. Сформулюйте правило важеля М.Є.Жуковського. 12. Що розуміють під зведеною сипаю (момен­том) і зведеною масою (моментом інерції). 3 яких умов їх визначають. Чи можна використати прави­ло важеля М.Є.Жуковського для визначення зведеної сили. 13. Чому зведена маса (або момент інерції), наприклад, для важільного механізму змінюється із зміною положення ланки зведення, а для зубчастого механізму сили. Чи змінюється зведена маса при зміні швидкості ланки зведення. 14. Запишіть рів­няння руху машини в формі інтегралу енергії та диференціальній формі. На підставі якого закону одер­жують ці рівняння? 15. Періоди руху машини. Що називають холостим ходом машини? Запишіть рів­няння руху для кожного з періодів. 16. Дайте визначення механічного ККД і коефіцієнта втрат. Чи може механічний ККД реальної машини бути більшим або рівним одиниці. Чим відрізняється миттєвий ККД від циклового. 17. Чим характеризується ефективність використання енергії в машинах. 18. Як визначити ККД машини, якщо відомі ККД окремих механізмів, що входять до її складу? 19. Як визначи­ти методом Віттенбауера дійсну швидкість руху ланки зведення?

Розділ 5