Побудова положень ланок механізму і траєкторій окремих точок

<7 8 91011 12 13 >

Для розв'язання задачі про положення ланок механізму (планів механізму) задаються кінематична схема механізму (розміри всіх його ланок) і закон руху початкової (початкових) ланки. У практиці інженерних розрахунків при кінематичному дослідженні механізмів, як правило, приймають рух початкової ланки лінійним, тобто рівномірним (w₁ =const або s₁ = const). Такий рух, як правило, вимагається умовами роботи механізму і приблизно таким він здійснюється на практиці. Це допущення не порушує загальності методів дослідження, тому що при нерівномірному русі вони залишаються в силі. Крім цього, при кінематичному дослідженні всі ланки механізму умовно вважають абсолютно твердими тілами, тобто розміри ланок незмінні, а зв'язки між ними ідеальні (в кінематичних парах відсутні зазори), всі ланки виготовлені абсолютно точно. Такі допущення дозволяють значно спростити методи дослідження механізмів, а одержані при цьому результати у багатьох випадках мало відрізняються від дійсних.

Побудову положень ланок плоский механізмів можна здійснити методами засічок, кругових шаблонів і геометричних місць.

Метод засічок. Побудову положень ланок цим методом розглянемо на прикладі кривошипно-повзунного механізму, кінематична схема і закон

руху кривошипа ОА ( w₁ =соnst) якого задані (рис. 3.1).

Побудову здійснюватимемо в певному масштабі. Для цього скористуємося масштабним коефіцієнтом,під яким розуміють відношення фізичної величини (шляху, швидкості тощо) до довжини відрізка, який цю величину зображає на кресленні (рисунку). Масштабний коефіцієнт, який у подальшому Будемо називати „масштабом", позначимо літерою m з індексом тієї величини, яка зображена графічно. Наприклад, при зображенні лінійних розмірів механізму масштаб буде визначатися за формулою

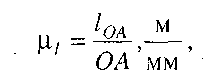
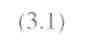
де 1_0А - дійсна величина кривошипа ОА, м; ОА - довжина відрізка ОА, мм, який зображує його на рис. 3.1.

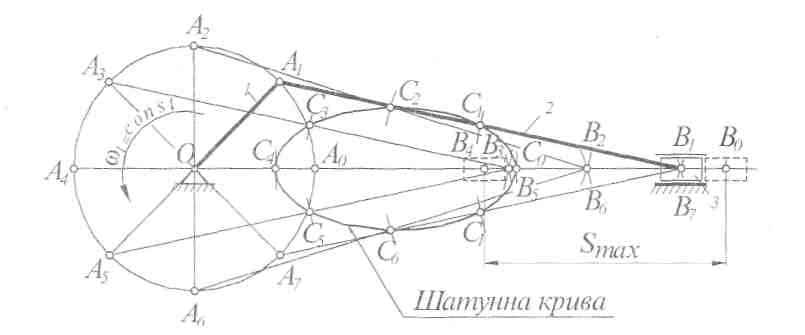
Рис. 3.1. Побудова положень ланок механізму і траєкторії точки С

Щоб знайти методом дугових засічок положення всіх точок і ланок механізму, необхідно послідовно розглянути рух кожної ланки від початкової до вихідної, у такому порядку, як вони приєднуються до механізму. Кривошип ОА здійснює рівномірний обертовий рух (w₁=соnst) навколо нерухомого центра О. Шатун АВ здійснює складний рух: центр шарніра А рухається по колу радіуса ОА, центр шарніра В - по прямій разом із повзуном, який зв'язаний із шатуном АВ і рухається вздовж нерухомої напрямної. За початкове положення механізму виберемо таке, за якого кривошип і шатун витягнуться в одну лінію ОА₀В₀. У центральному кривошипно-повзунному механізмі ця лінія збігається з напрямком руху центра шарніра В. Далі, поділимо траєкторію точки А на довільно вибране число рівних частин, наприклад 8, як це показано на рис. 3.1, точки поділу позначимо А₀,А₁,А₂,...,А₇ у напрямку обертання кривошипа. Тобто перехід з одного положення в інше здійснюється за час T/8, де Т - період обертання кривошипа (Т=60/п, с; п - частота обертання кривошипа, хв^_1).

Положення точки В знайдемо методом дугових засічок, враховуючи, що довжина шатуна А В протягом руху залишається незмінною. Для цього з одержаних точок А₀,A₁,A₂,...,A₇ радіусом АВ зробимо дугові засічки на траєкторії точки B, у результаті чого знайдемо положення центрів шарніра В - В₀,В₁,В₂,...,В₇ . З'єднавши точки А_i і B_i, відрізками A_i,B_i_,одержимо положення шатуна АВ і повзуна В (i=0, 1, 2, ..., 7).

Таким самим способом побудуємо траєкторію точки С, яка лежить на шатуні АВ (див. рис. 3.1). Для цього з точок А_i зробимо на відповідних положеннях шатуна A_i B_i дугові засічки радіусом АС. З'єднавши послідовно одержані точки С_i плавною кривою, одержимо траєкторію точки С. Через те, що точка С лежить на шатуні, її траєкторію називають шатунною кривою. Форма цієї кривої залежить від положенні точки С на шатуні АВ. Шатунні криві широко використовуються в сучасній техніці для виконання певних рухів виконавчими органами різних механізмів і машин, при проектуванні механізмів з вистоями, заданими передаточними функціями тощо.

Якщо до складу механізму входять кілька груп, то побудова їхніх планів здійснюється аналогічно. Спочатку будують ряд положень кривошипа ОА, потім ланок першої приєднаної групи і, визначивши положення точки під'єднання другої групи, дуговими засічками знаходять положення ланок другої приєднаної групи. Побудову планів положень механізму закінчують побудовою положень ланок останньої групи.

Початковим положенням кривошипа ОА вибирають таке положення, за якого одна з вихідних ланок (у нашому випадку повзун В) займатиме одне з крайніх (мертвих) положень.

Побудова діаграм переміщення.При дослідженні механізмів часто недостатньо знайти тільки форму шляху - траєкторію руху точки; треба ще знати характер зміни величини пройденого шляху залежно від часу або кута повороту кривошипа (узагальненої координати). Для цього будують діаграми лінійних s=s(t) або кутових B=B(t) переміщень, якщо ланка здійснює коливальний рух.

Розглянемо побудову діаграми переміщень повзуна В (рис. 3.2) для кривошипно-повзунного механізму, схема якого зображена на рис. 3.1.

Якщо рух початкової ланки прийнято рівномірним, то це означає, що за рівні проміжки часу кривошип повертатиметься на однакові кути; переміщення повзуна будуть вимірюватися відрізками В₀В_i, де і = 0, 1, 2,..., п - положення механізму.

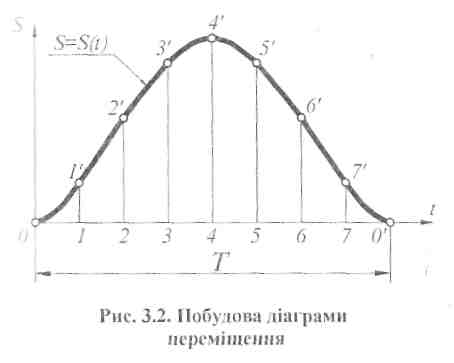
Рис. 3.2. Побудова діаграми переміщення

Будують прямокутну систему координат (див. рис. 3.2): на осі абсцис відкладають відрізок l = 0 - 0', який зображає в масштабі m_t=Т/l, с/мм, період Т (час) одного обороту кривошипа ОА (або кут ф₁ =2П); на осі ординат - лінійні переміщення повзуна В у масштабі m_s=S_m_ах/[S_m_ах], де S_m_ах - максимальний хід повзуна В, м; [S_m_ах] - відрізок, мм, на діаграмі, який зображує цей хід. У нашому випадку [S_m_ах] = 44'.

Відрізок l ділять на таку кількість відрізків 0-1, 1-2,...,7-0', на яку розбита траєкторія точки А (у даному випадку на 8). Точки 0,1,2,...,7 відповідають моментам часу, коли механізм займатиме відповідно положення 0, 1, 2,...,7. Тоді на відповідних ординатах відкладають у вибраному масштабі m_s, м/мм, переміщення точки В від крайнього положення В₀ за певні проміжки часу. Якщо масштаби довжини на рис. 3.1 і переміщень на рис. 3.2 рівні, то відрізки 1-1’, 2-2',...,7-7' на діаграмі будують відповідно рівні відрізкам В₀В₁ В₀B_2……,В₀ B₇ на плані механізму. Одержані точки 0, 1’, 2',...,7' з'єднують плавною кривою, яка і буде діаграмою переміщень повзуна В - s=s(t).

Якщо ланка здійснює коливальний рух, то, як правило, будують діаграму кутових переміщень залежно від часу або кута ф₁. Масштаб кутових переміщень виражається аналогічно: m_B=B_m_ах / [Bmах] де Bmах - максимальний кут розмаху ланки, рад або град., [B_m_ах] - максимальна ордината, мм, яка зображує на діаграмі цей кут.

Метод кругових шаблонів наведено в підручнику [13], геометричних місць (фіктивних положень) - [1, 11].

<7 8 91011 12 13 >

Дата добавления: 2016-06-15; просмотров: 4101;