Структурна класифікація плоских механізмів

У сучасному машинобудуванні особливо широко поширені плоскі механізми, ланки яких входять до пар IV і V класів. Розглянемо принци­пи їхньої структурної класифікації.

Структурна класифікація механізмів, основи якої були закладені Л. В. Ассуром і далі розвинуті І. І. Артоболевським, В. В. Добровольським та іншими радянськими вченими, є однією з найраціональніших класифі­кацій плоских механізмів. Перевагою цієї класифікації є те, що вона пов'язується з методами кінематичного, силового та динамічного дослід­ження механізмів.

В основу структурної класифікації механізмів покладено основний принцип утворення механізмів, який полягає у тому, що будь-який меха­нізм можна одержати шляхом приєднання до механізму І класу структур­них груп, умовою існування яких є рівність (2.10) або (2.11).

Якщо врахувати, що в плоских механізмах переважно використо­вуються кінематичні пари V класу, а кінематичні пари IV класу, що вхо­дять до складу плоского механізму, можна замінити парами V класу (див. п. 2.5), тому залежність (2.10) можна переписати так:

3n-2p₅ = 0,

звідки

р₅= п. (2.12)

Оскільки числа ланок і пар можуть бути тільки цілими, то умову (2.12) задовольнятимуть тільки такі сполучення чисел ланок і кінематич­них пар, що входять у групу:

Характерно, що до складу структурної групи може входити тільки парне число ланок.

Вибираючи різні сполучення цих чисел, які відповідають умові (2.12), можна дістати групи різного виду. Всі добуті таким способом групи можна поділити на класи. Як це буде показано далі, поділ груп на класи зумовлений методами кінематичного і силового аналізів, властивими групам кожного класу.

Структурні групи і механізми ІI класу. Як видно з наведе­ного вище, найпростішою групою буде група, яка складається з двох ланок і трьох кінематичних пар V класу (рис. 2.28, а). Така група дістала назву структурної групи (групи Лссура) II класу II порядку, або двоповідкової групи.Порядок групи визначається кількістю елементів пар, якими група приєднується до основного механізму. У групі, що зображена на рис. 2. 28, а, вільні елементи мають дві пари (В і О), якими група може приєднуватися до інших ланок.

Групи II класу бувають п'яти видів залежно від кількості оберто­вих і поступальних пар та їхнього взаємного розташування. Назвемо гру­пу, яка має дві ланки і три обертові пари, I видом групи II класу.

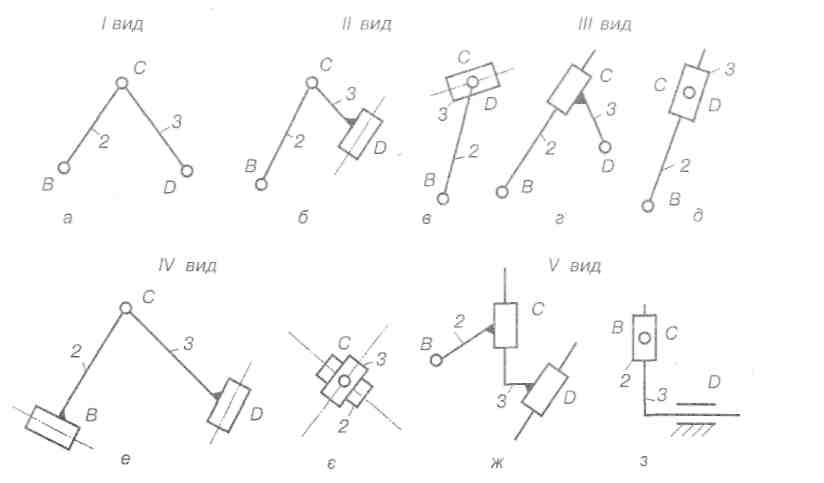
Рис. 2.28. Структурні групи II класу

Усі інші види груп II класу можна одержати заміною окремих обертових пар поступальними. Якщо одну з крайніх обертових пар замі­нити поступальною, одержимо групуII виду(рис. 2.28, б, в). Група, зображена на рис. 2. 28. в, є частковим випадком групи, зображеної на рис. 2.28, б, у якій довжина відрізка CD=0. III видгрупи II класу зображено на рис. 2.28, г, д (на рис. 2.28, д СD=0). Тут поступальною замінено середню обертову пару. Якщо замінити дві крайні обертові пари поступальними, то одержимо групу II класу IV виду(рис. 2.28, є, є). На рис. 2.28, є відрізки ВС=СП~0. І, нарешті, у групі V виду(рис. 2.28, ж, з) поступальними замі­нені крайня і середня обертові пари (на рис. 2.28,з ВС=0). При заміні всіх обертових пар поступальними одержимо клиновий механізм (W = 1).

На рис. 2.29 і 2.30 показано приклади найпростіших механізмів, у яких використовуються групи II класу всіх п'яти видів.

а б в

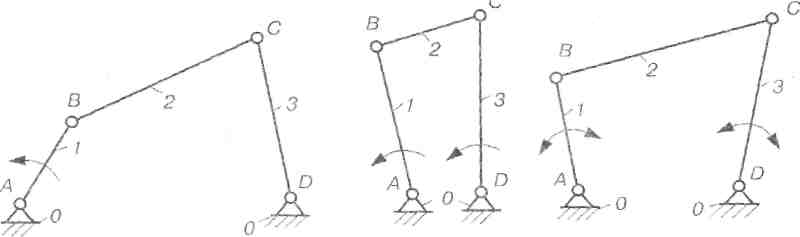
Рис 2.29. Чотириланкові механізми, одержані з використанням структурної групи ІI класу І виду

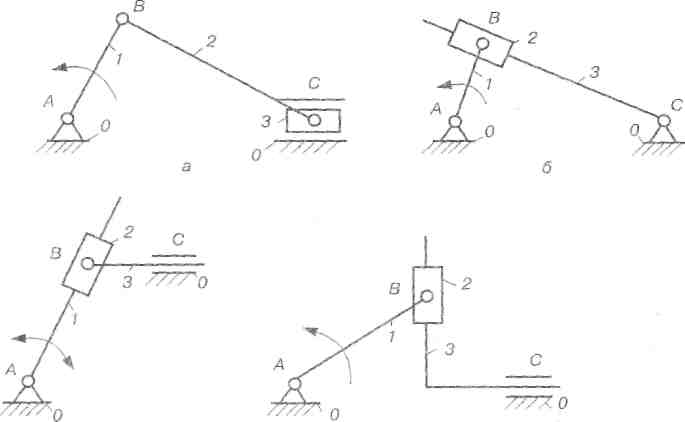
Рис. 2.30. Чотириланкові механізми, одержані з використанням інших видів структурних груп II класу

На рис. 2,29, а зображено шарнірний чотириланковий механізм АВСD з ланками: 0 - стояк, 1 - кривошип, 2 - шатун, 3 - коромисло. Лан­ка 1, яка повертається на 360° навколо нерухомої осі, називається кри­вошипом.Ланка 2, яка утворює кінематичні пари тільки з рухомими лан­ками, називається шатуном.Ланка 3, яка здійснює коливальний рух, -коромислом.Шарнірний чотириланковий механізм, залежно від розмірів ланок, може бути трьох видів: кривошипно-коромисловий(рис. 2.29, а), двокривошипний(ланки 1, 3 здійснюють повний поворот, рис. 2.29, б), двокоромисловий(ланки 1, 3 коливаються, рис. 2.29, в).

Прикладом механізму, де використовується група II класу II виду є кривошипно-повзунний (або коромислово-повзунний) механізм (рис. 2.30, а); III виду - кривошипно-кулісний механізм (рис. 2.30, б); IV виду - тангесний механізм (рис. 2.30, в); V виду - синусний механізм (рис. 2.30, г).

Механізми, до складу яких входять тільки групи II класу, нази­ваються механізмами II класу.Більшість механізмів, які застосовують­ся у сучасній техніці, належать до механізмів цього класу.

Структурні групи і механізми III класу. Розглянемо друге мож­ливе сполучення кількостей ланок і кінематичних пар, що утворюють структурну групу (n=4, Р₅=6). Неважко побачити, що для цього сполучен­ня можна дістати три типи кінематичних ланцюгів, структурні принципи утворення яких різні.

Перший кінематичний ланцюг (рис. 2.31, а) складається з ланки З (базисної), яка входить у три кінематичні пари з ланками 2, 4, 5 (повідки). Та­кий кінематичний ланцюг є групою III класу III порядку, або триповідковою групою. Приєднання цієї групи до основного механізму здійснюється за допо­могою трьох повідків (елементи кінематичних пар В, F, G вільні).

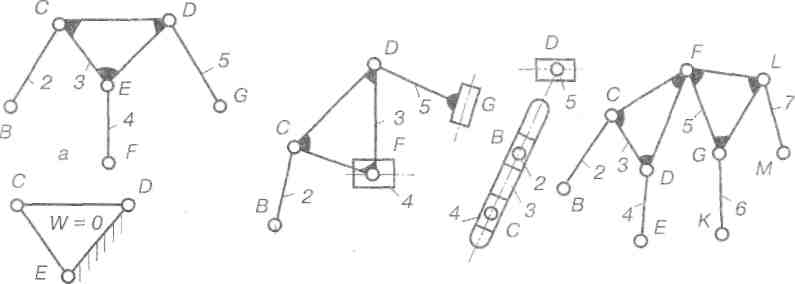
Рис. 2.31. Структурні групи III класу

Особливістю цієї групи є наявність у ній ланки 3, що входить у три кінематичні пари і утворює деякий жорсткий трикутний контур який ніби скла­дається з трьох ланок ЕС, СD, DЕ, що входять до складу трьох кінематичних пар (рис. 2.31, б). Відносний ступінь вільності такого контуру W = 0.

Групи III класу можуть бути різних видів, які одержують шляхом заміни обертових пар поступальними. Приклади таких груп показані на рис. 2.31, в, г. Очевидно, що кількість видів груп III класу значно більша, ніж II класу. Групи IIIкласу можуть у своєму складі мати кількість ланок більше чотирьох і пар більше шести (рис. 2.31, д).

Механізми, до складу яких входять групи, невищі за групи III класу, називаються механізмами III класу. Приклади таких механізмів зображені на рис. 2. 32.

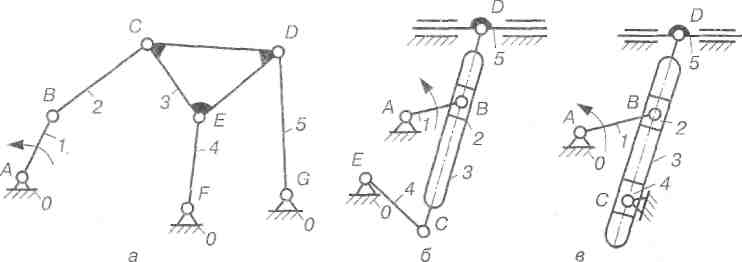
Рис. 2.32. Приклади шестиланкових механізмів III класу

Структурні групи і механізми IV класу. Другий можливий кіне­матичний ланцюг з чотирьох ланок і шістьох нижчих пар показано на рис 2.33, а. Характерною особливістю цієї групи є те, що до її складу входить чотири­кутний рухомий контур DЕFG (рис. 2.33, б), відносний ступінь вільності якогоW = 1. Група, до складу якої входить чотирикутний замкнутий рухомий контур, належить до групи IV класу.Отже, група, зображена на рис. 2.33, а буде групою IV класу IIпорядку, тому що вона приєднується до основного механізму віль­ними елементами кінематичних пар В, С. На рис. 2.33, в зображено приклад механізму, до складу якого входить ця група.

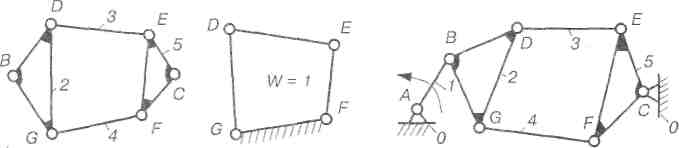
а б в

Рис. 2.33. Група (а), контур (б) і механізм (в) IV класу

Механізми, до складу яких входять групи не вище IV класу, нази­вається механізмами IV класу.

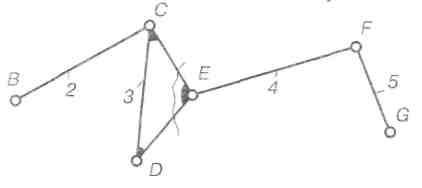
Третій можливий вид кінематичного ланцюга з чотирьох ланок і шести кінематичних пар показано на рис, 2.34. Неважко побачити, що цей ланцюг розпада­ється на дві групи II класу (групу 2-3 і групу 4-5). Тобто цей ланцюг не дає нової групи. Рис. 2.34. Кінематичний ланцюг, який скла­дається з двох груп II класу

 

Коли перейти до подальших сполучень ланок і пар, які задовольня­ють умови структурної групи, то можна побачити, що до складу груп V класу увійде п'ятикутний контур (W=2), до складу труп VI класу - шестикут­ний (W=3) і т. д. На основі зазначеного, можна зробити такі висновки: до складу групи ПІ класу_ входить так званий контур III класу (див. рис. 2.32), групи IV класу - контур IV класу (див. рис. 2.33) тощо.

Клас контурувизначається кількістю кінематичних пар, до скла­ду яких входять ланки, що його утворюють (рис. 2.35).

Клас групивизначається найвищим класом контуру, що входить до її складу.

Клас механізмувизначається найвищим класом груп, що входять до його складу. Наприклад, якщо механізм утворений двома групами - групою III класу і групою IV класу, то його треба віднести до механіз­мів IV класу.

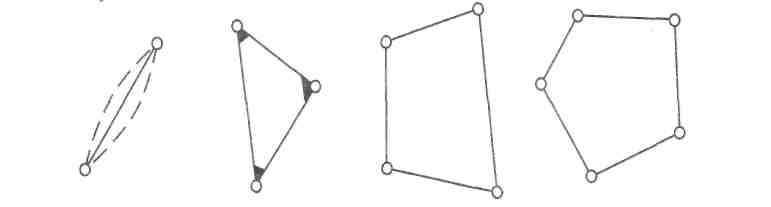
II III IV V

Рис.2.35. Клас контуру

Визначаючи клас механізму, необхідно вказувати, які з ланок є по­чатковими, бо залежно від добору початкових ланок можна змінювати клас механізму. Наприклад, якщо у механізмі, схему якого зображено на рис. 2.32,а, за початкову ланку прийняти не ланку 1, а ланку 4 або 5, то весь механізм буде механізмом II класу, що утворений двома групами II класу (у першому випадку - групами 3-5 і 2-1 , у другому - групами 3-4 і 2-1).

Склад і послідовність приєднання структурних груп механізму можуть бути виражені формулою будови механізму. Наприклад, формули будови для механізмів, які зображені:

на рис. 2. 29, 2.30 - I(1) -> II (2,3) ;

нарис. 2.32 - I(1) -» III

нарис. 2.33,в - I(1) -> IV (2,3,4,5),

де І - механізм І класу; II, III, IV - клас груп. Номера ланок, що входять до складу механізму І класу або структурних груп, указані в дужках. У групі III класу окремо виділена базисна ланка.

Якщо до складу механізму поряд з нижчими парами входять ще й вищі пари, то, користуючись методом заміни вищих пар (див. п. 2.5), замі­нюють такі пари нижчими, після чого визначають клас механізму.