Дослідження руху механізмів методом кінематичних діаграм

<8 9 101112 13 14 >

Маючи діаграму (графік) переміщень будь-якої точки або ланки механізму як функцію шляху .9 залежно від часу і, методом графічного диференціювання можна визначити швидкості і прискорення точки (ланки), рух якої розглядають

Для побудови діаграми швидкостей v=v(t) використовують залежність

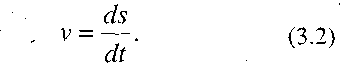
Як відомо, похідна функції s=s(t) у точці А (рис.3.3) визначається тангенсом кута нахилу дотичної до цієї кривої s=s{t), яка проведена через точку А.

З урахуванням масштабів побудови діаграми s=s(t) можна записати, що

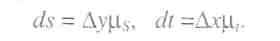
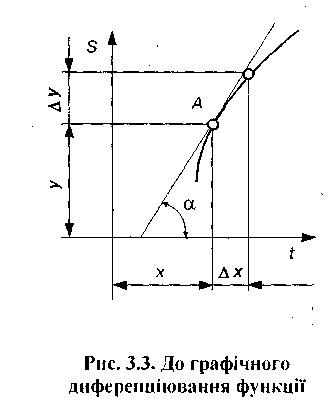
Рис. 3.3. До графічного диференціювання функції

Тоді залежність (3.2) набуде вигляду

де 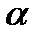- кут нахилу дотичної у т 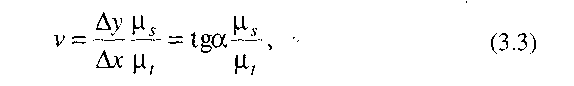очці А діаграмми s=s(t); 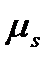, 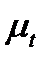- масштаби діаграми по осі ординат і осі абсцис відповідно.

Із залежності (3.3) видно, що швидкість руху точки в будь-якому положенні пропорційно зв'язана з тангенсом кута нахилу дотичної, оскільки масштаби 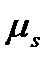, 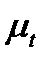є сталими величинами.

Таким чином, щоб побудувати діаграму швидкостей 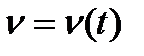, беруть ряд точок на діаграмі s=s(t) і через них проводять дотичні. Знайшовши тангенс кутів нахилу цих дотичних у відповідних положеннях, будують діаграму 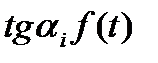Ця діаграма одночасно буде діаграмою швидкостей у деякому масштабі, який можна знайти, використовуючи залежність (3.3).

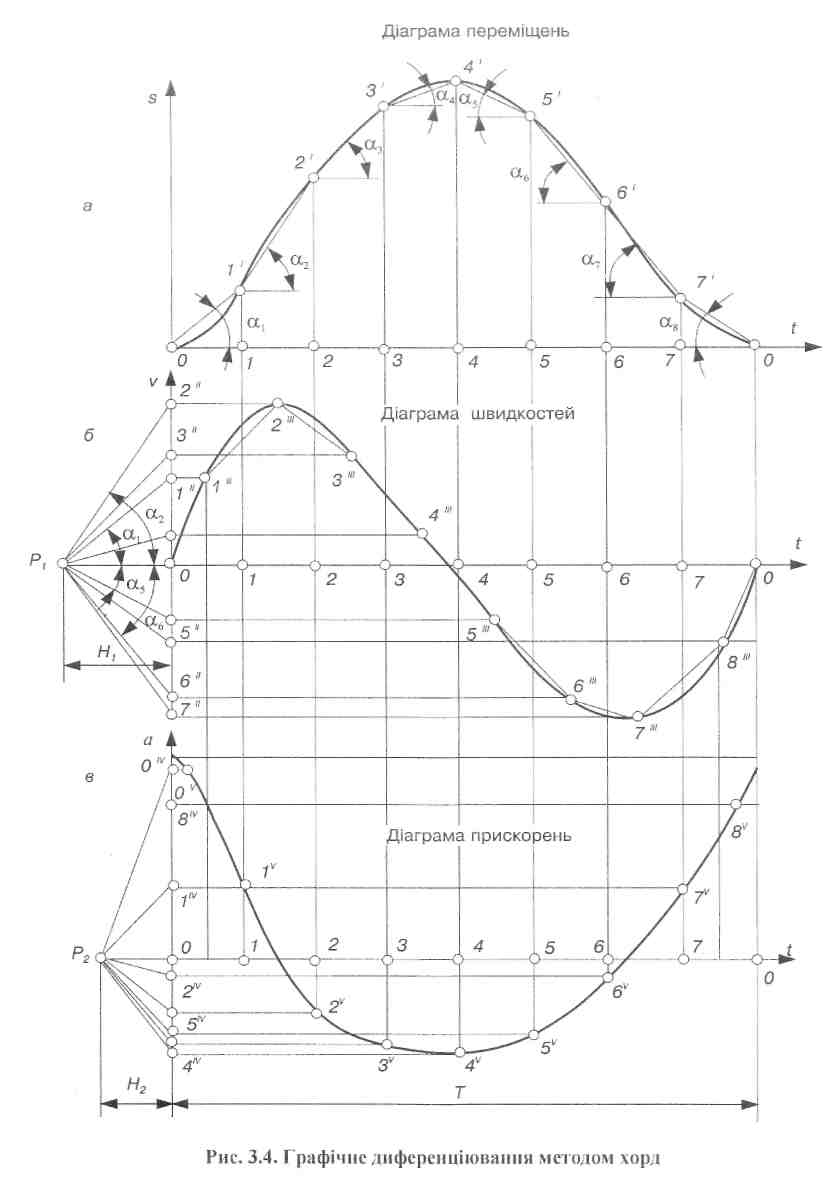
Для побудови діаграм швидкостей і прискорень можуть використовуватися два методи - дотичних і хорд.

Надалі розглянемо лише метод хорд оскільки метод дотичних досить незручний, бо дуже важко точно проводити дотичні до кривих і добитися стабільних результатів. Тому на практиці більшого поширення набув метод хорд, який ґрунтується на відомій теоремі про кінцевий приріст функції: якщо функція та її перша похідна безперервні, то на будь-якому інтервалі, наприклад 0-1 (рис. 3.4, а), хорда 0-1’, яка стягує дугу, буде паралельна дотичній до кривої s=s(t) хоча б в одній точці, що лежить у середині цього інтервалу. Тому при цьому методі на діаграмі s=s(t), замість дотичних проводять хорди 0-1, 1-2', 2'-3',...,7-0 (рис. 3.4, а), а на діаграмі 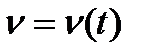(рис. 3.4, б) із точки Р₁ - промені Р₁-1", P₁-2", P₁- 3",..., Р₁-7” які паралельні відповідним хордам, до перетину з віссю ординат 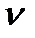. Відрізки 0-1”, 0-2", 0-3",..., 0-7" у масштабі 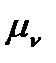визначають значення швидкостей десь посередині відповідних інтервалів часу.

Масштаб швидкостей 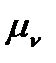можна визначити, використавши залежність (3.3), в яку треба підставити

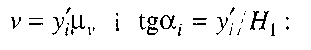
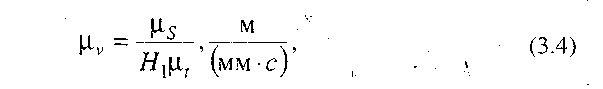
де 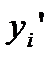- відрізки 0-1",0-2",...,0-7" (див. рис. 3.4,6).

Із залежності (3.4) видно, що за допомогою відрізка Я, можна змінювати масштаб побудови діаграми швидкостей.

Для спрощення побудови діаграм відрізки 0-1", 0-2", 0-3",. ..,0-7" відкладають посередині відповідних інтервалів часу. Точки 0, 1"’, 2'", З'",...,7^’" з'єднують плавною кривою і одержують з певною точністю діаграму швидкостей 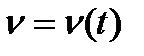. Чим менший інтервал часу розглядається, тобто чим більше проведено хорд тим більше наближаються до заданої кривої. Особливу увагу треба звернути на ділянку, де крива, яку диференціюють, має екстремум. У цьому місці криву треба розділити на менші ділянки (проміжки часу). Значення швидкостей у відповідних положеннях механізму визначаються відповідними ординатами діаграми 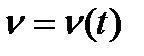помноженими на масштаб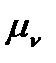

Маючи діаграму швидкостей 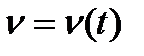, аналогічно будують діаграму прискорень а=а(t), виходячи із того, що

Отже, щоб побудувати діаграму прискорень, необхідно продиференціювати діаграму швидкостей за часом, провівши відповідно на діаграмі 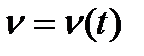хорди 0-1", 1",-2'" і т. д., а з точки Р₂ діаграми прискорень відповідні промені Р₂-0^І^V, Р₂-1^IV і т. д., які паралельні цим хордам. Масштаб прискорень 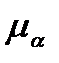визначається за формулою

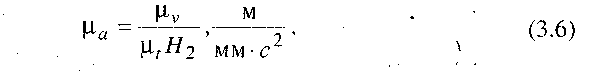
де Н₂ - довжина відрізка 0Р₂ на діаграмі прискорень.

Аналогічно будують діаграми кутових швидкостей і кутових прискорень при заданій діаграмі кутових переміщень ланки.

Порівнюючи побудовані графіки переміщень, швидкостей і прискорень (рис. 3.4), можна встановити між ними такі залежності:

1) зростанню ординат кривої, що диференціюється, відповідають додатні значення ординат диференціальної кривої, а зменшенню - від'ємні значення;

2) при максимумі кривої, що диференціюється, диференціальна крива переходить через нуль від додатних значень ординат до від'ємних, а при мінімумі - від від'ємних значень ординат до додатних;

3) точці перегину кривої, що диференціюється, відповідає максимум або мінімум на диференціальній кривій.

3.4. Дослідження руху механізмів методом планів швидкостей і прискорень

Розглянутий метод графічного дослідження механізмів при всій його простоті та наочності не розв'язує повністю питання кінематики механізмів. Побудовані діаграми переміщень, швидкостей і прискорень дають уявлення лише про скалярні кінематичні величини руху однієї точки (або ланки), напрямки ж векторів цих величин залишаються невідомими Кінематичні параметри швидкості та прискорення точки можна визначати за допомогою графічного диференціювання лише після того, як побудовані її траєкторія і графік переміщень.

У практичному застосуванні при дослідженні руху механізмів досить точним і зручним є графоаналітичний метод, що ґрунтується на побудові планів швидкостей і прискорень. Перевагою цього методу є те, що в результаті побудови планів одержують не тільки величини, але й напрямки швидкості та прискорення заданих точок механізму. Теоретичні основи побудови планів швидкостей і прискорень розглядаються в курсі теоретичної механіки. Згадаємо деякі з положень, необхідні для побудови планів швидкостей і прискорень [9, 17].

Плани швидкостей.Візьмемо будь-яке тіло К, що здійснює плоский рух. Положення твердого тіла в загальному випадку визначається трьома точками А, В, С (рис. 3.5, а), які незмінно зв'язані з тілом і утворюють жорсткий трикутник АВС (на рис. 3.5, а заштрихований).

Нехай відомі швидкості 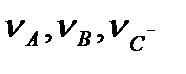відповідно точок А, В, С і положення миттєвого центра швидкостей Р . Вектор швидкості будь-якої точки направлений перпендикулярно до радіуса-вектора, який з'єднує цю точку з точкою Р , тобто

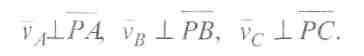
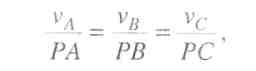
Швидкості точок пропорційні відповідним радіусам:

тому що

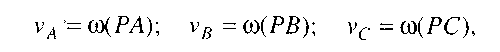
де w - миттєва кутова швидкість тіла К .

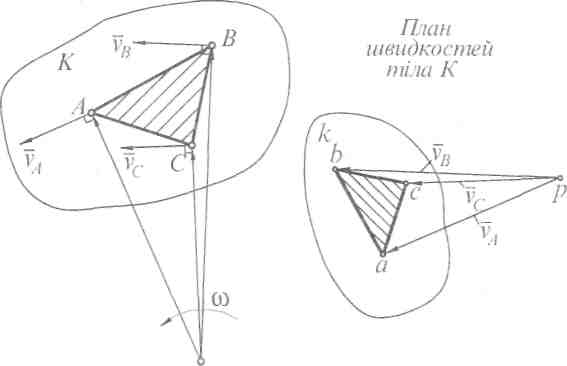
Рис. 3.5. До побудови плану швидкостей тіла

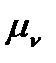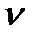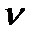Візьмемо тепер будь-яку довільну точку р на площині (рис. 3.5, б) і побудуємо в деякому масштабі з цієї точки вектори швидкостей точок А, В, С. З'єднавши прямими точки а, b і с - кінці векторів швидкостей _а, _в, 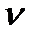_с - одержимо план швидкостейтіла АВС. Якщо таким чином побудувати вектори швидкостей усіх крайніх точок тіла К і з'єднати їх між собою, то на плані швидкостей одержимо фігуру k , яка буде подібна до тіла К . Отже, планом швидкостей будь-якого твердого тіла (ланки) є геометричне місце кінців векторів швидкостей крайніх точок цього тіла, які відкладені з однієї довільної точки, що називається полюсом плану швидкостей

У зв'язку з тим, що відрізки ра, рb, рс перпендикулярні радіусам РА, РВ, РС і пропорційні їм, вся фігура раbс подібна фігурі РАВС і повернута відносно неї на 90° в бік миттєвого обертання. Це характерно й для фігури аbс, яка подібна фігурі АВС .

Звідси одержимо теорему подібностідля планів швидкостей.

План швидкостей твердого тіла (ланки) подібний тілу і повернутий відносно нього на 90° у бік миттєвого обертання тіла.

Теорема подібності справедлива тільки для незмінної системи твердого тіла (ланки) - і ні в якому випадку для механізму в цілому, який є змінною системою. Для механізму, який складається з системи ланок і який при русі постійно міняє свою форму, можна лише мати сукупність планів швидкостей окремих ланок, що побудовані з одного полюса, спільного для всіх ланок. Такий рисунок називають планом швидкостей механізму.

План швидкостей аbс тіла АВС (рис. 3.5) розташований однаково з цим тілом, тобто, якщо обходити план швидкостей і тіло в одному напрямку, наприклад від точок а і А за годинниковою стрілкою, то порядок літер буде однаковий: аbс і АВС. Крім того, якщо вибрати аb-АВ і накласти план швидкостей аbс на тіло АВС, то відповідні точки плану збігаються з точками тіла, а полюс р плану швидкостей збігатиметеся з точкою Р - миттєвим центром швидкостей тіла К. Тому план швидкостей ще називають зображенням тіла.

Надалі позначатимемо точки ланок великими літерами {А, В, С,...), а їхні зображення на плані швидкостей - малими (а, b, с,...). Плани швидкостей механізму можна будувати методом подібності, використовуючи теорему подібності, і методом векторних рівнянь. Але через те, що плани прискорень можна будувати тільки методом векторних рівнянь, далі розглянемо більш детально останній

В основі методу векторних рівняньлежить теорема про розклад складного руху на два прості: переносний івідносний.

Для прикладу побудуємо план швидкостей кривошипно-повзунного механізму (рис 3.6), для якого задані кінематична схема і закон руху кривошипа ОА (w₁=const). Якщо задана частота обертання n₁(хв^-1), то для визначення кутової швидкості скористаємося залежністю w₁ = .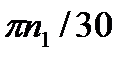

План швидкостей. Розв'язування задачі розпочнемо з визначення швидкості точки А початкової ланки: 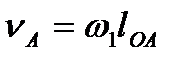(1_0А - дійсна довжина кривошипа ОА, м).

Вектор 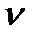_А направлений перпендикулярно до кривошипа ОА в бік його руху. Зобразимо цей вектор відрізком ра (рис. 3.6, б), який у масштабі визначає величину цієї швидкості: 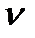_А=(ра) .

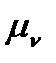Щоб знайти швидкість точки В, яка є спільною для шатуна А В і повзуна В, згадаємо теорему про розклад складного руху на переносний і відносний. Шатун АВ здійснює складний рух, який можна розкласти на два прості: переносний (поступальний) зі швидкістю 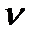_А точки А і відносний (обертовий) відносно точки А зі швидкістю 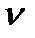_ВА.

б в

Рис. 3.6. Побудова планів швидкостей та прискорень кривошипно-повзуного механізму:

а) кінематична схема механізму; б) план швидкостей; в) план прискорені.

Дійсно, якщо надати кривошипу елементарне переміщення 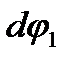, то центр шарніра А переміститься в точку А₁, шарніра В - у точку B₁. При такому русі шатун АВ здійснює складний рух: точка А рухається дугою кола, точка В - прямою лінією. Нехай спочатку всі точки шатуна АВ рухаються, як точка А, зі швидкістю 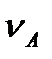, при цьому вісь шатуна займе положення А₁ В₁^’. Потім, прийнявши точку А₁, за нерухомий центр (полюс), повернемо шатун А В так, щоб точка В₁^’ потрапила на свою дійсну траєкторію х-х, тобто в точку В₁ .

Отже, при заміні дійсного руху шатуна АВ двома умовними, що дає такий самий кінцевий результат переміщення, центр шарніра В набув послідовно дві швидкості: при поступальному русі - 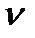_А, при обертовому - відносну швидкість 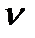_ва точки В відносно точки А, яка невідома нам за величиною, але відома за напрямком (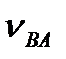 АВ). На основі цього запишемо векторне рівняння для знаходження швидкості точки В:

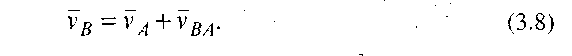
Для визначення векторів швидкостей 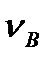і 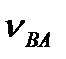проведемо через точку а (рис. 3.8, б) лінію, яка показує напрямок вектора відносної швидкості, а з полюса р лінію, паралельну руху повзуна В (|| х-х), точка перетину цих ліній визначить точку b - кінець векторів 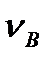і 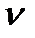_ва. Відрізок аb не тільки визначає у масштабі величину (модуль) відносної швидкості 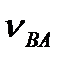= =(аb) 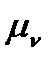, але й одночасно він є планом швидкостей шатуна АВ. А тому точка С, яка лежить на ньому, згідно теореми подібності, на плані лежатиме на відрізку аb. Склавши пропорцію

знайдемо довжину відрізка

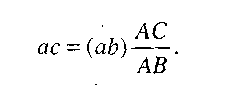
Відкладемо відрізок ас на плані швидкостей і, з'єднавши точку с з полюсом p, знайдемо швидкість точки С: 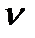_с = (рс) .

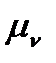Планом швидкостей кривошипа О А буде відрізок ра (точка О, як нерухома, потрапила в полюс р), повзуна В - точка b (всі точки повзуна мають однакову швидкість ).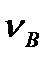

Знайшовши лінійні швидкості всіх ланок механізму, можна встановити їхні кутові швидкості. У даному випадку кутова швидкість шатун AB

де 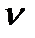_ВА = (аb) .

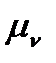Для визначення напрямку кутової швидкості w₂ перенесемо вектор швидкості 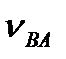у точку В (рис.3.6, а) і розглянемо рух точки В відносно точки А у напрямку швидкості 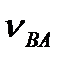. У нашому випадку кутова швидкість w₂ напрямлена за рухом годинникової стрілки.

План прискорень. Плани прискорень будують аналогічно планам швидкостей.

Планом прискорень будь-якого твердого тіла (ланки) називають геометричне місце кінців векторів прискорень крайніх його точок, які відкладені з однієї довільної точки, що називається полюсом плану прискорень.

Теорема подібності для планів прискорень формулюється так

План прискорень будь-якого тіла (ланки) подібний тілу і повернутий відносно нього на деякий невизначений кут. А тому плани прискорень можна побудувати тільки методом векторних рівнянь.

Розглянемо методику побудови планів прискорень на прикладі кривошипно-повзунного механізму (див. рис. 3.6). Вихідними даними для побудови плану прискорень є положення ланок механізму (план механізму) і план швидкостей. Рівняння, які використовуються при побудові плану прискорень, відрізняються тільки тим, що повні прискорення точки розкладають на певні складові. У даному випадку (рис. 3.6, а) повне прискорення точки А є геометрична сума нормального (доцентрового) і дотичного (тангенціального) прискорень:

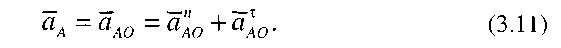
Нормальне прискорення a 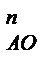напрямлене по лінії АО до центра обертання кривошипа О, дотичне а 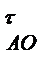- перпендикулярно до АО і направлене в бік напрямку кутового прискорення 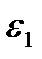ланки 1. Модулі цих прискорень находять із співвідношень:

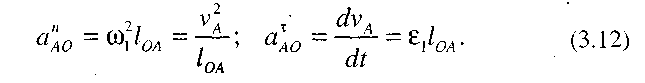
Якщо початкова ланка обертається рівномірно (w₁=const), то 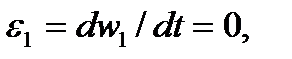а значить у даному випадку a 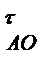=0, тобто прискорення точки а_А =а^п_А0.

Прийнявши деяку точку 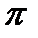за полюс плану прискорень (рис. 3.6, в), відкладемо вектор, який зображує нормальне прискорення точки А, у вигляді відрізка а. Тоді масштаб (масштабний коефіцієнт) прискорень знайдемо із співвідношення

Прискорення точки В найдемо з рівняння, аналогічного рівнянню (3.8):

де вектор прискорення а_в напрямлений уздовж напрямної х-х. Розкладаємо відносне прискорення а_ВА на дві складові:

Тоді рівняння (3.14) запишемо у такому вигляді

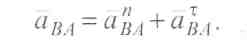
Вектор нормального прискорення а^п_ВА направлений уздовж лінії ВА від точки В до А, а його модуль

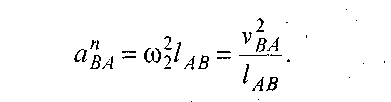
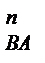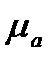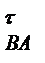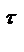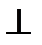На плані прискорень а зображено відрізком ап = а / , який прикладемо своїм початком у точці а (згідно з правилом складання векторів). Через його кінець (точку п) проведемо лінію дотичного прискорення а , що направлене перпендикулярно до лінії АВ (а _ВАа 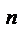_ВА), через полюс 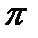- напрямок прискорення точки В (|| х-х), тоді точка перетину напрямків прискорень 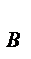а і а 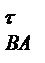визначить точку b - кінець векторів а_B і а 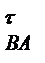. З'єднавши точки а і b, знайдемо вектор повного прискорення 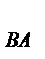a 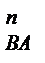=a +a 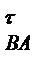, і цим самим побудуємо план прискорень шатуна AB.

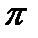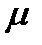Положення точки с на плані прискорень можна знайти методом подібності, склавши пропорцію (3.9), з якої визначають відрізок ас. Тоді прискорення точки С становить а_с - ( с) _а .

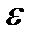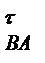Модуль кутового прискорення ланки 2 ₂ = а /l 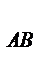. Для визначення напрямку 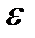₂ перенесемо вектор дотичного прискорення а 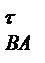у точку В (рис. 3.6, а) і спостерігатимемо, в який бік цей вектор буде обертати шатун АВ відносно вибраного полюса (точки А). У нашому випадку кутове прискорення 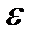₂ напрямлене проти руху годинникової стрілки. Отже, рух шатуна АВ в цьому положенні сповільнений, оскільки кутова швидкість W 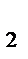має інший напрямок.

3.5. Приклади побудови планів швидкостей і прискорень механізмів II класу

3.5.1. Плани швидкостей і прискорень шарнірного чотириланкового механізму[18]. Як і для кривошипно-повзунного механізму, повинні бути задані кінематична схема механізму (рис. 3.7, а) і закон руху початкової ланки - кривошипа 1 (w₁ =сonst).

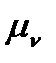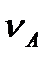
План швидкостей.Визначимо модуль швидкості точки А: V_А = w₁l_0А і відкладемо вектор цієї швидкості у масштабі ( 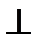OA), попередньо вибравши відрізок ра (рис. 3.7, б). Масштаб плану швидкостей одержимо за формулою (3.7).

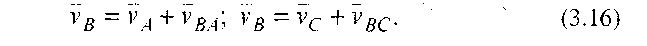
Для визначення швидкості точки В, яка одночасно належить ланкам 2 і 3, складемо векторні рівняння:

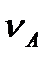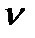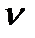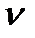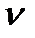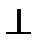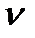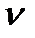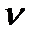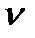За першим рівнянням (3.16) через кінець вектора (точка а) проведемо лінію відносної швидкості _ва точки В відносно точки А ( _ВААВ), а через точку р - лінію відносної швидкості _BC точки В відносно точки С ( _ВСВС). Точка С, як нерухома ( _с=0), потрапляє в полюс плану швидкостей, там знаходиться і точка О ( _о=0). Точка перетину ліній-напрямків швидкостей _ВА і _вс = 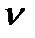_B визначає точку b, а значить і величину цих векторів у масштабі 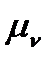: 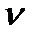_ВА = (а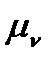b) , _B=(р b) .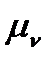

Швидкість точки D, яка належить ланці 2, можна встановити, використавши теорему подібності для плану швидкостей, згідно з якою можна записати такі пропорції:

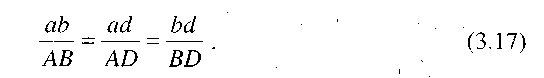
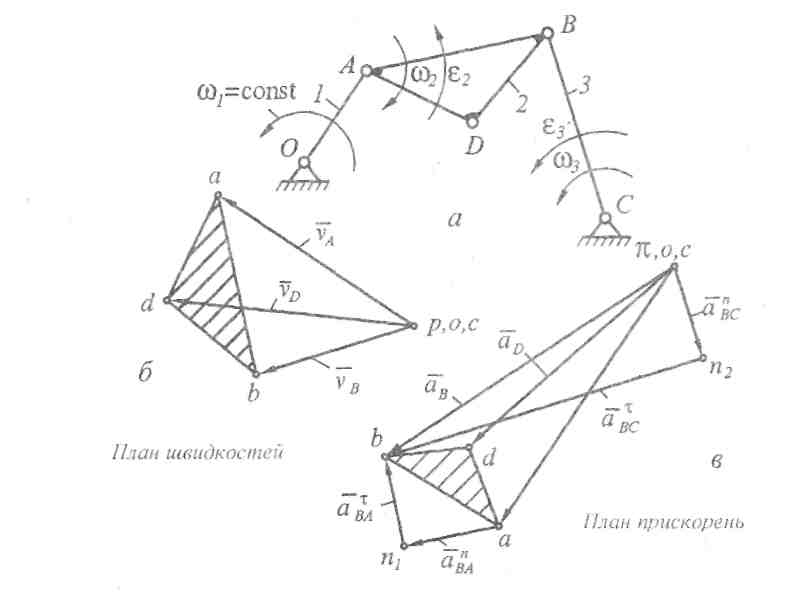
Рис. 3.7. Побудова планів швидкостей та прискорень шарнірного чотириланкового механізму:

а) кінематична схема механізму; б) план швидкостей; в) план прискорень

З цих пропорцій знайдемо відрізки:

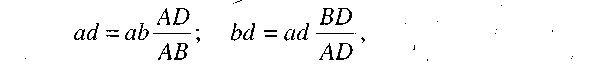
за допомогою яких побудуємо трикутник аbd, подібний трикутнику АBD. З'єднавши точку d з полюсом р, отримаємо швидкість точки D: 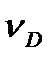= {рd) 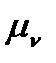. Ії можна визначити також методом векторних рівнянь, розглянувши швидкість точки D через швидкості точок А і В, тобто записавши рівняння:

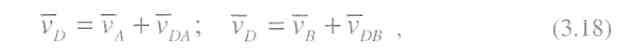
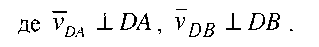
Кутові швидкості ланок 2 і 3 знайдемо, використавши відносні швидкості V_BA і V_BC :

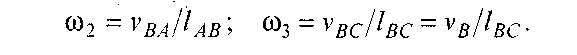
Щоб встановити напрямок кутової швидкості w₂ , перенесемо вектор 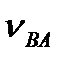у точку В і розглянемо рух ланки 2 відносно точки А; для кутової швидкості w₃ - перенесемо вектор 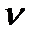_вс також у точку В і розглянемо рух ланки 3 відносно точки С. У даному випадку w₂ направлена за годинниковою стрілкою, w₃ - проти руху годинникової стрілки.

План прискорень.Побудову плану прискорень цього механізму також розпочнемо з ланки 1. Прискорення точки А при w₁ = соnst визначимо за формулою нормального прискорення: а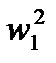_А = І_ОА.

Вибравши полюс плану прискорень 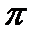(рис. 3.7, в), відкладемо від нього відрізок 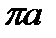, який відповідає прискоренню точки А у масштабі 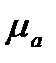(3.13). Прискорення точки А спрямоване по лінії АО від точки А до точки О (до центра обертання кривошипа).

Для знаходження прискорення точки В складемо два векторні рівняння:

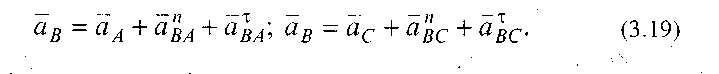
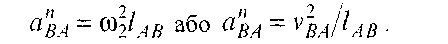
Згідно з першим рівнянням системи (3.19) до кінця вектора а_Апотрібно прикласти початок вектора а^п_ВА нормального прискорення точки В відносно точки А, величина якого встановлюється за формулою

У вибраному масштабі цей вектор зображений відрізком 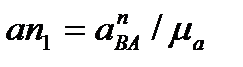(мм). Прискорення а 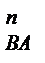направлене по осі ланки АВ від точки В до точки А. Через точку згідно з цим самим рівнянням необхідно провести лінію-напрямок дотичного прискорення а 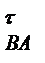, величина останнього невідома, відомий лише його напрямок - перпендикулярно до лінії АВ.

Розглянемо друге рівняння (3.19). Прискорення точки С дорівнює нулю, тому точка с збігається з полюсом плану. Прискорення а = 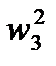І_ВС і направлене від точки В до точки С. Відрізок 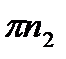= сп₂ = 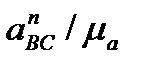який відповідає прискоренню 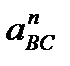на плані відкладаємо від точки 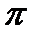. Через точку п₂ проведемо лінію-напрямок дотичного прискорення 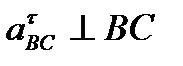до перетину з лінією-напрямком прискорення а 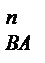. Точка перетину b цих ліній визначить величину і напрямок прискорення точки В та величини дотичних прискорень (у масштабі .).

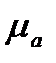Прискорення точки D знайдемо методом подібності, побудувавши подібний ланці АВD трикутник аbd . Відрізки ас і bd визначимо із пропорцій (3.17). Щоб знайти прискорення точки D, можна також записати векторні рівняння, виразивши прискорення точки D через прискорення точок А і В, тобто

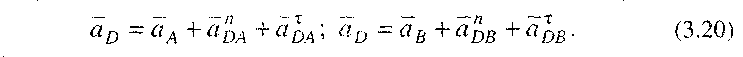
Плани прискорень на основі рівнянь (3,20) будуються так само, як і для точки B (3.19).

Модуль кутових прискорень ланок 2 і 3 знайдемо за формулами

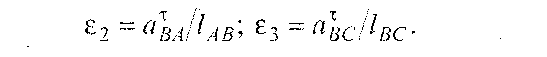
Для визначення напрямку 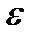₂ і 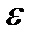₃перенесемо вектори 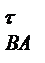а і а 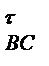у точку В і розглянемо, в який бік ці вектори повертають відповідно ланки АВ і ВС.

3.5.2. Плани швидкостей і прискорень кулісного механізму. На рис. 3.8, а зображено кінематичну схему кривошипно-кулісного механізму.

План швидкостей Швидкість обертання кривошипа приймаємо w₁=const. Тоді швидкість точки А, яка належить кривошипу 1 і повзуну 2,визначається за формулою V_А = w₁ І_OA і спрямована перпендикулярно до лінії ОА. Відкладаємо вектор цієї швидкості у масштабі 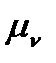(3.7), попередньо вибравши відрізок ра (рис. 3.8, б).

Для визначення швидкості точки А₃ , яка належить кулісі 3 і в даний момент збігається з точкою А, можна використати теорему про розклад складного руху повзуна 2 на два прості - переносний (обертовий) разом із кулісою 3 і відносний (поступальний) рух уздовж куліси 3. У переносному русі швидкість точки А, яка належить повзуну 2, буде дорівнювати швидкості точки А₃, у відносному русі - швидкості 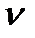_AAпоступального руху повзуна вздовж осі куліси. На підставі цього запишемо векторне рівняння:

Крім цього, оскільки точка А₃ належить кулісі 3, то можна записати друге векторне рівняння:

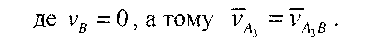
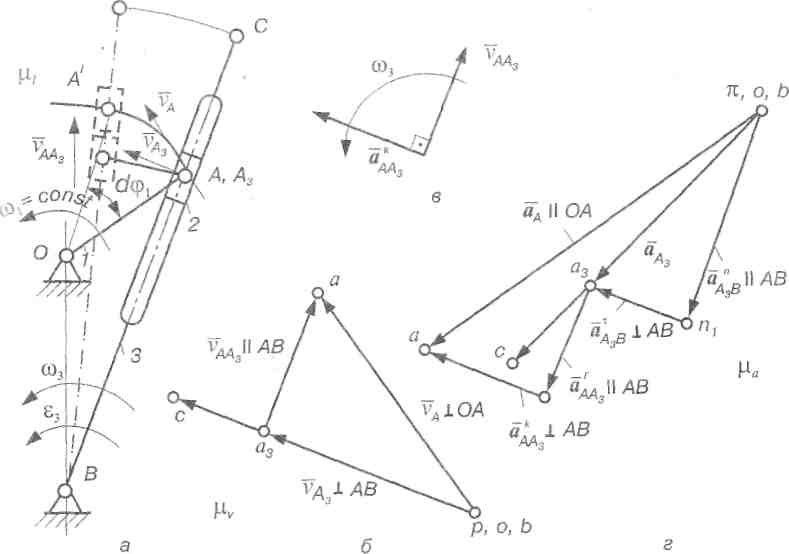
Рис. 3.8. Побудова планів швидкостей та прискорень кривошипно-кулісного механізму:

а) кінематична схема механізму; б) план швидкостей; в) напрям коріолісового прискорення;

г) план прискорень

Провівши через полюс р лінію-напрямок вектора 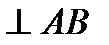(рис.3.8, б), а через точку а - лінію-напрямок вектора 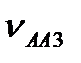, знайдемо точку а₃ перетину цих векторів. Тоді 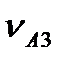= (pa₃ ) 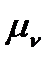, 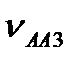=(aa₃) 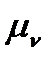. Напрямки швидкостей 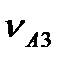і 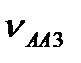визначаються рівнянням (3.21).

Швидкість точки С, яка належить кулісі 3, можна встановити методом подібності, склавши пропорцію:

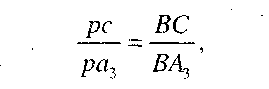
звідки маємо

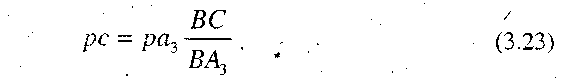
Тоді швидкість точки С

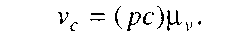
Знайдемо кутові швидкості ланок. Очевидно, що

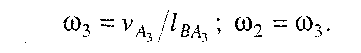
Напрямок кутової швидкості w₃ можна визначити, якщо вектор швидкості точки Аз (рис. 3.8, а) прикласти в точці А₃ і розглянути обертання ланки 3 навколо точки В. У даному випадку w₃ напрямлена проти руху годинникової стрілки.

План прискорень. План прискорень механізму будується в такому самому порядку (рис 3.8, г). Прискорення точки A визначимо за формулою:

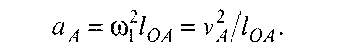
Вибравши полюс плану прискорень 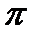, відкладемо від нього відрізок 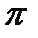а, який відповідає прискоренню точки А у масштабі 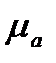(3.13). Прискорення точки А спрямоване по лінії ОА від точки А до точки О.

Для визначення прискорення точки А₃ використаємо теорему Коріоліса, згідно з якою, якщо переносний рух тіла обертовий(звідси відносний рух - поступальний), то абсолютне прискорення точки дорівнює векторній сумі трьох прискорень: переносного, відносного і коріолісового(поворотного). У даному випадку переносний рух (рух куліси 3) обертовий, тому можна записати:

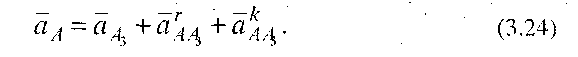
Прискорення точки a_A₃ є прискорення в переносному русі повзуна 2 разом із точкою A₃, повна його величина

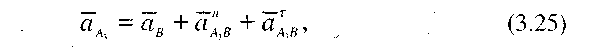
де а_B - прискорення точки В (а_B = 0); 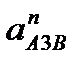= 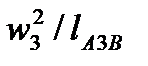-нормальне прискорення точки А₃ при обертанні куліси 3 навколо точки В, вектор якого направлений вздовж лінії А₃В від точки А₃ до точки В; а 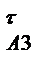- дотичне прискорення точки А₃ при обертанні куліси 3 навколо точки В.

Відносне (релятивне) прискорення 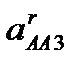направлене вздовж осі куліси АзВ. Його величина (модуль) - невідома.

Модуль прискорення Коріоліса визначається за формулою (для плоского руху)

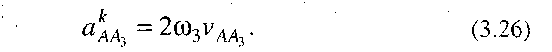
Щоб знайти його напрямок необхідно вектор відносної швидкості 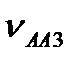(рис. 3.8, в) повернути на 90° у бік переносної кутової швидкості.

Підставивши (3.25) у (3.24), одержимо

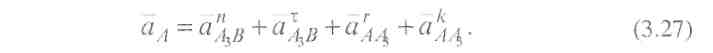
На основі рівняння (3.27) побудуємо план прискорень механізму. З точки 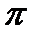відкладемо відрізок 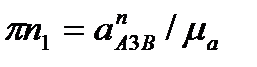який у масштабі 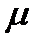_а визначає вектор прискорення а^п_А_B, а через точку n₁ проведемо лінію-напрямок дотичного прискорення а 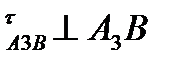. Оскільки величини прискорень 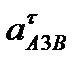і 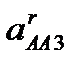невідомі, побудову планів прискорень продовжимо з кінця векторного рівняння, приклавши вектор а 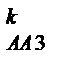своїм кінцем у точку а (відрізок kа = 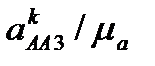), а через початок цього вектора проведемо лінію-напрямок вектора а 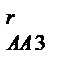до перетину з вектором а 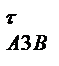. точка a₃перетину яких визначить величину повного прискорення а_А3, а також невідомих складових а 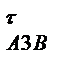і 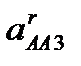напрямки яких одержимо за (3.27). 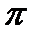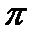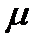Положення точки с на плані прискорень отримаємо методом подібності, використавши рівняння (3.23), у яке замість точки p підставимо , тоді а_с = ( с) _а.

Модуль кутового прискорення ланки 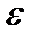3 ₃ = 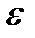₂ знайдемо за формулою 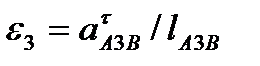Щоб встановити його напрямок, вектор 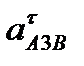перенесемо в точку А₃ і будемо спостерігати обертання ланка 3 навколо точки В. У даному випадку кутове прискорення 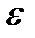₃ буде направлене проти руху годинникової стрілки.

При побудові планів швидкостей і прискорень кулісних механізмів, як правило, вибирають за переносне середовище не кулісу 3, а повзун 2. У такому випадку рівняння (3.21), (3.22), (3.24) і (3.25) набувають вигляду:

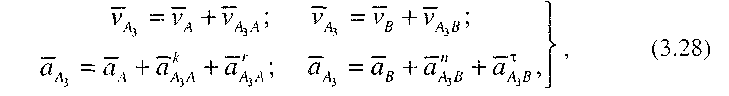
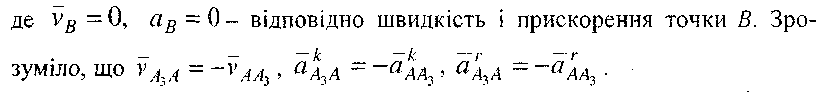
3.5.3. Плани швидкостей і прискорень шарнірного шестиланкового механізму. Як і для інших механізмів, повинні бути задані кінематична схема механізму (рис. 3.9, а) та закон руху початкової ланки - кривошипа 1 (w₁=соnst).

План швидкостей. Швидкість точки 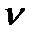А _а = 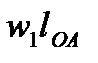. Вибравши масштаб плану швидкостей 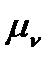(3.7), визначаємо величину відрізка ра, який на плані швидкостей (рис. 3.9, б) показує цей вектор .

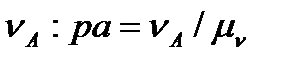Для знаходження швидкості точки В записуємо векторні рівняння:

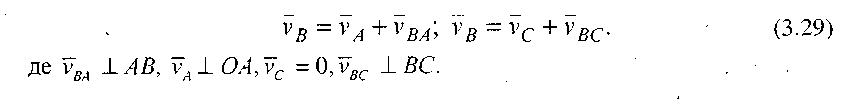
На основі цих рівнянь будуємо план швидкостей, з якого знаходимо швидкості 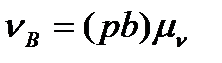, 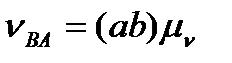. Швидкість точки О знаходимо методом подібності, складаючи пропорцію