Структурні формули кінематичних ланцюгів

Основи теорії структури кінематичних ланцюгів закладені в праці видатного російського вченого професора П.І.Сомова, опублікованій у 1887 р., і розвинуті радянськими вченими. Будемо дотримуватися в основ­ному методів, які розроблені ними [1].

Раніше було встановлено, що коли на рух ланки у просторі не накладено ніяких умов зв'язку, то вона має шістьступенів вільності. Тоді, якщо число ла­нок кінематичного ланцюга дорівнює k, то загальне число ступенів вільності які мають k ланок до їхнього з'єднання в кінематичні пари, дорівнює 6k. Кожна кі­нематична пара накладає різне число зв'язків на.відносний рух ланок, що зале­жить від класу пари (див. п. 2.1). Позначимо число пар І класу, що входять до складу ланцюга,. Через р₁ П -р₂, III - рз, IV –р₄ V-р₅. Клас кінематичної пари ви­значається числом умов зв'язку, які накладає кожна кінематична пара на віднос­ний рух ланок (див. табл. 2.1). Для визначення загального числа ступенів вільнос­ті ланок кінематичного ланцюга треба з 6k ступенів вільності, що їх ланки мали до того як увійшли до кінематичної пари, вилучити ті ступені вільності, які від­німають кінематичні пари. З табл. 2.1 видно, що одна пара І класу накладає на відносний рух ланок одну умову зв'язку (S= 1), II класу-дві (S=2) іт.д. Тоді число ступенів вільності Н, що їх має кінематичний ланцюг

Н = 6k- 5р₅ - 4р₄ - Зр₃ - 2р₂ –р₁. (2.3)

Оскільки в механізмах одна ланка нерухома, тому при вивченні руху всіх ланок механізму їхні абсолютні переміщення розглядаємо як та­кі, що відбуваються відносно однієї з ланок, прийнятої за нерухому. Якщо одна з ланок кінематичного ланцюга буде нерухомою, то загальне число ступенів вільності ланок ланцюга зменшиться на шість, тобто число ступенів вільності (рухомості) відносно нерухомої ланки

W = Н -6. (2.4)

Підставляючи у (2.4) замість Н його вираз з (2.3), одержимо

W= 6(k - 1) - 5р₅ -4р₄ -3p₃ -2р₂ –р₁. (2.5)

Якщо в (2.5) величину k-1 позначити п, то дістанемо

W = 6п - 5р₅-4р₄ - Зр₃ - 2р₂ –р₁, (2.6)

де п - число рухомихланок кінематичного ланцюга.

Формула (2.6) має назву формули рухомостіабо структурної формули кінематичного ланцюга загального вигляду.

Формула (2.6) вперше, у дещо іншому вигляді, була одержана проф. П.І. Сомовим і розвинута проф. А.П. Малишевим, а тому носить назву формули Сомова - Малишева.

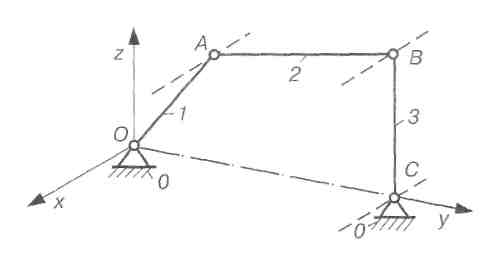
Рис. 2.20. Шарнірний чотириланковий механізм з паралельними осями шарнірів

Виберемо систему ко­ординат хуz так, щоб напрям осі х збігався з напрямом осей пар, а осі у і z лежали у пло­щині, перпендикулярній до осей пар. Тоді неважко пере­конатися, що в цьому випадку ланки механізму ОАВС руха­тимуться паралельно загальній площині, яка містить осі у і z, тобто маємо так званий плоский механізм. Які загальні обмеження накладено на рухи всіх ланок механізму умовою паралельності осей всіх кінематичних пар. Ці обмеження будуть такі. Ланки механізму не можуть мати обертового руху навколо осей у і z і поступального руху вздовж осі х, тобто з шести можливих рухів три не можуть бути здійснені.

Якщо на рух усіх ланок механізму в цілому накладено три загальні обмеження, то, очевидно, цю обставину треба взяти до уваги, підраховуючи ступені вільності окремих ланок і рухомості механізму в цілому. Дійсно, якщо в загальному випадку число ступенів вільності рухомих ланок механізму дорі­внює 6n, то для плоского механізму - (6 - 3)п = 3n, тобто тіло в плоскому русі має три ступеня вільності (два поступальні вздовж осей у і z, один обертовий навколо осі х). Відповідно з п'яти зв'язків, які накладає пара V кла­су, у цьому механізмі вона накладатиме тільки 5 - 3 = 2, бо три зв'язки вже накладено умовою паралельності осей пар, і т. п. Структурна формула ме­ханізму (2. 6) тоді перепишеться так:

W = (6 - 3)n - (5 - 3)р₅ - (4 - 3)р₄- (3 - 3)р₃.

Тобто ступені вільності(рухомості) плоского механізму

W=3п-2р₅-р₄ (2.7)

Це є структурна формула для плоских механізмів загального вигляду, або формула Чебишева.

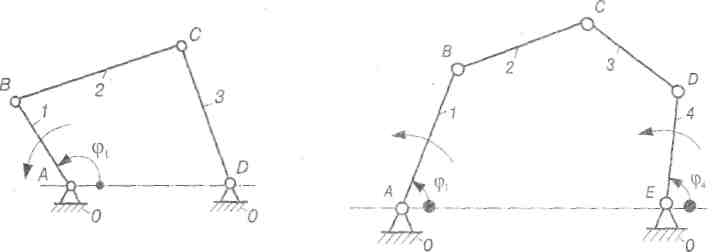
Рис. 2.21. Шарнірний чотириланковий Рис. 2.22 Шарнірний пятиланковий

Механізм механізм

Ланка, якій приписують одну або кілька узагальнених координат, називається початковоюЦей термін пов'язаний з тим, що знаходження положень усіх ланок механізму починають із знаходження положень поча­ткових ланок.

Для кінематичного ланцюга, схему якого зображено на рис. 2.22, ступінь вільності (п = 4, р₅ = 5 , р₄ = 0)

W=3 *4-2*5-0 = 2.

Якщо в цьому ланцюгу задано лише положення ланки АВ, то оче­видно, що положення решти рухомих ланок буде невизначеним. Коли ж задати ще положення іншої ланки, наприклад, ланки 4, кутом ф₄, то всі лайки механізму будуть мати цілком визначений рух Отже, у механізмі, зображеному на рис. 2.22, повинно бути дві початкові ланки,

Таким чином, ступені вільності кінематичного ланцюга відносно стояка визначають кількість початкових ланок механізму. Останні можуть збігатися з вхідними ланками механізму, а можуть і не збігатися. Добір початкової ланки визначається зручністю визначення по­ложень ланок механізму, зручністю його аналізу.

На основі наведеного можна показати, як із кінематичного лан­цюга одержати механізм. Для цього необхідно одну з ланок ланцюга зробити нерухомою (стояком), підрахувати ступені вільності і залежно від їхньої кількості одній або кільком ланкам задати закон руху (див. рис. 2.21, 2. 22).

Початкові ланки надалі будемо показувати круговими (або пря­мими) стрілками.

2.4. Зайві ступені вільностій умови зв'язку

Під час дослідження структури механізмів можуть виявитися сту­пені вільності та умови зв'язку, що не впливають на рухомість механізму в цілому. Такі ступені вільності й умови зв'язку називають зайвими.Як приклад, на рис. 2.23 зображено схему кулачкового механізму до скла­ду якого входить 0 - стояк, 1 - кулачок, 2 - штовхач, 3 - ролик.

Стояк і кулачок утворюють обертову пару V класу, кулачок і ро­лик - пару IV класу, штовхач і стояк - поступальну пару V класу, штовхач і ролик - обертову пару V класу. Тоді, виходячи з числа рухомих ланок і кінематичних пар, ступінь вільності механізму за формулою Чебишева:

W = 3n - 2р₅ - р₄ = 3 * 3 - 2 * 3 - 1 = 2.

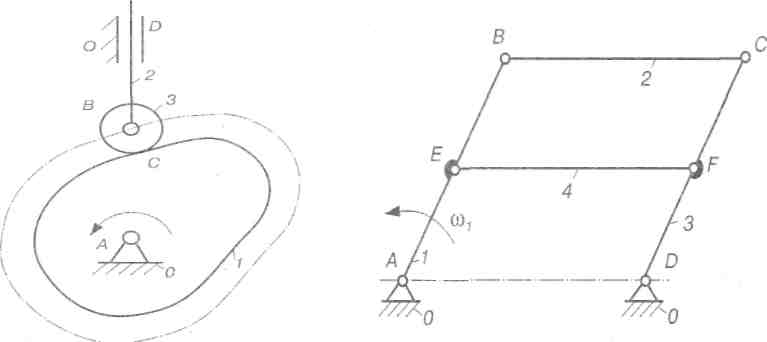
Рис. 2.23. Кулачковий Рис. 2.24. Механізм паралелограма