Основний принцип утворення механізмів

Основний принцип утворення механізмів, який вперше був сфор­мульований у 1914 р. російським вченим Л.В. Ассуром, розкриває не тіль­ки методику утворення механізмів шляхом послідовного приєднання кінематичних ланцюгів, але й становить основу найраціональнішої класифі­кації механізмів. Цей принцип полягає в наступному.

Будь-який механізм можна одержати, якщо до початкової ланки (або початкових ланок) і стояка послідовно приєднувати кіне­матичні ланцюги з нульовим ступенем вільності.

Справді, як це було показано вище, до складу кожного механізм}' вхо­дять нерухома ланка (стояк), початкові ланки, тобто ланки, закони руху яких за­дано і від яких залежать закони руху всіх інших ланок Отже, приступаючи до створення механізму бажаного ступеня вільності, закріпляємо одну з ланок (утворюємо стояк) і вводимо у кінематичні пари з цією ланкою початкові ланки за кількістю ступенів вільності, які повинен мати механізм. При цьому кожна по­чаткова ланка повинна мати тільки один ступінь вільності.

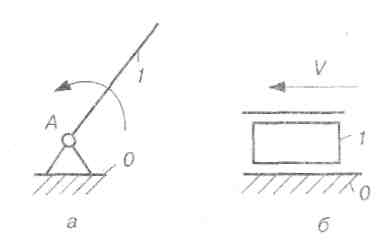
Рис. 2.26. Механізми І класу:

а) з кривошипом; б) з повзуном

Назвемо умовно початкову лапку і стояк, які утворюють кінематичну пару V класу, механізмом І класу. На рис. 2.26 зображено механізми І класу, початкові ланки яких утворюють із стояком обертову (рис. 2.26, а) або поступальну (рис. 2.26, б) пару. Щоб одержати механізм потрібного ступеня вільності, необхідно до механізму (механізмів) ї класу приєднати систему ла­нок, яка становить один або кілька кінема­тичних ланцюгів з нульовим ступенем вільності. Остання умова випливає з того, що весь механізм повинен мати ступінь вільності, що дорівнює сумі ступенів вільності механізмів 3 класу. Як приклад, розглянемо плоский механізм, зображений на рис. 2.27. Ступінь вільності цього механізму можна визначити за формулою Чебишева

W = Зn - 2р₅ -р₄ =3*5 - 2*7 - 0= 1,

де число рухомих ланок п = 5 , число пар V класу р₅=7 і число пар IV кла­су р₄= 0.

Якщо прийняти стояк 0 і ланку 1 за механізм І класу (рис. 2.27, б), то ланки 2-5 утворюють систему ланок, що мають нульовий ступінь віль­ності (n = 4, р₅ = 6).

Неважко побачити, що кінематичний ланцюг з ланок 2-5 можна поділити на два кінематичні ланцюги: один, що складається з ланок 2-3 (рис. 2.27, в), і другий, що складається з ланок 4-5 (рис. 27.2,г). Кожний з цих кінематичних ланцюгів, що складається з двох ланок і трьох кінема­тичних пар V класу, має ступінь вільності W_гр, який дорівнює нулю. Роз­бити ці ланцюги на простіші кінематичні ланцюги, що мали б нульовий ступінь вільності, неможливо.

Кінематичний ланцюг, який після приєднання його вільними елементами кінематичних пар до стояка, має нульовий ступінь віль­ності і який не можна роз'єднати на простіші кінематичні ланцюги нульового ступеня вільності, називається структурною групою або групою Ассура.

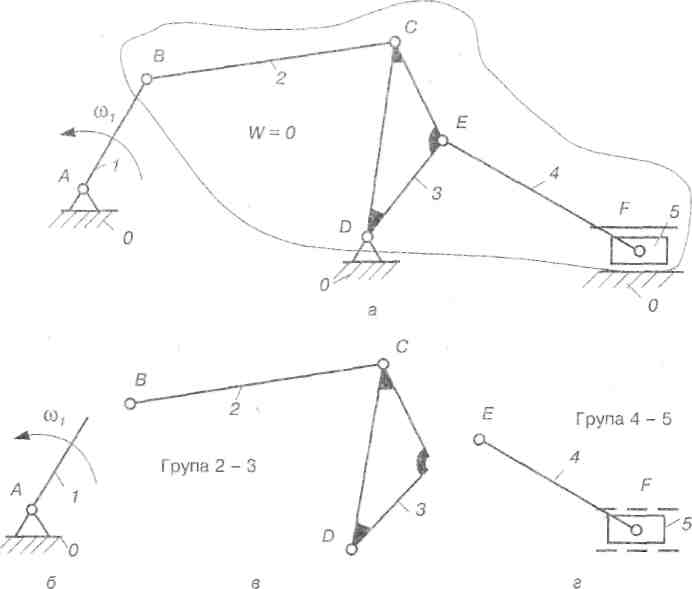
Рис. 2.27. До основного принципу утворення механізмів

Таким чином, плоский механізм, зображений на рис. 2.27,а, який має один ступінь вільності, можна розглядати як такий, що утворений спо­собом послідовного приєднання до механізму І класу двох груп: групи 2-3 і групи 4-5. Тепер молена дати таке визначення основному принципу утворення механізмів.

Будь-який механізм можна одержати, якщо до механізму (ме­ханізмів) І класу послідовно приєднувати структурні групи.

При послідовному приєднанні груп необхідно керуватися певними правилами. При утворенні механізму з одним ступенем вільності перша група приєднується вільними елементами ланок до початкової ланки і сто­яка. Наступні групи можуть приєднуватися до будь-яких ланок одержано­го механізму тільки так, щоб ланки групи могли рухатися одна відносно одної. Не можна групу всіма вільними елементами приєднувати до одної ланки, тому що у цьому випадку одержимо нерухомий контур.

Структурні групи плоских механізмів задовольняють умову

W_гр = 3п-2р₅-р₄ = 0; (2.10)

структурні групи просторових механізмів

W_гр = 6п - 5р₅-4р₄-Зр₃-2р₂-р₁ = 0. (2.11)

Як плоскі, так й просторові структурні групи використовуються не тільки при структурному синтезі, але й при аналізі механізмів.