Кінематичні пари та їхня класифікація

Кінематична пара є рухоме з'єднання двох ланок, які стикаються. Можливі з'єднання ланок у кінематичні пари дуже різноманітні. Напри­клад, на рис. 2.1 зображено так звану однорухому обертову (обертальну) кінематичну пару, в якій ланки А і В з'єднані за допомогою двох цилінд­ричних поверхонь. Бурти тіла А (вала) обмежують відносний поступаль­ний рух тіл вздовж осі х-х, але не заважають їхньому відносному оберто­вому (обертальному) руху. На рис. 2.2 зображено схему іншого способу сполучення елементів ланок А і В. Ця кінематична пара допускає відносне перекочування, ковзання і вертіння.

Таким чином, на відносний рух кожної ланки кінематичної пари накладаються певні обмеження, які залежать від способу сполучення ланок кінематичної пари. Ці обмеження будемо називати умовами зв'язкув кі­нематичних парах.

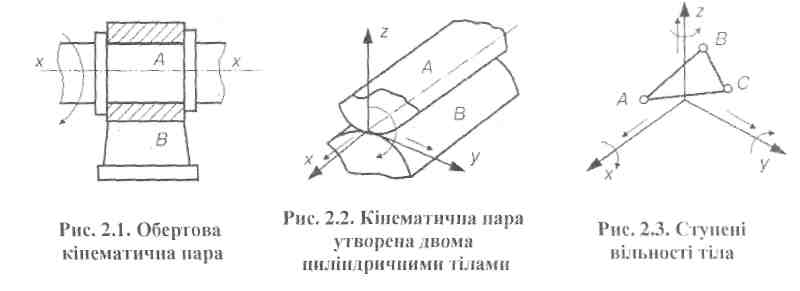
Які ж зв'язки і в якій кількості можуть бути накладені на віднос­ний рух ланок кінематичної пари? Як відомо, у загальному випадку всяке абсолютно тверде тіло АВС (рис. 2.3), що вільно рухається в просторі, має шість ступенів вільності. Рух такого тіла можна розглядати як обертан­ня навколо осей х, у, і та ковзання вздовж цих самих осей. Таким чином, тіло АВС матиме шість видів незалежних можливих рухів: три обертові і три поступальні.

Входження ланки в кінематичну пару з іншою ланкою накладає на відносні рухи цих ланок певні умови зв'язку. Очевидно, що число цих умов зв'язку може бути тільки цілим і меншим шести, бо вже у тому випадку, коли число умов зв'язку дорівнює шести, тіло втрачає відносну рухомість. Так само число умов зв'язку не може бути меншим за одиницю, бо у цьому випадку ланки не стикаються, тобто кінематична пара не існує, маємо два тіла, що вільно рухаються в просторі.

Таким чином, число умов зв'язку, накладених на відносний рух кожної ланки кінематичної пари, змінюється в межах від 1 до 5. Тоді число ступенів вільності H ланки кінематичної пари у відносному русі може бути виражене рівнянням

H = 6 - S, (2.1)

де S - число умов зв'язку, які накладає кінематична пара на відносний рух ланок.

З (2.1) випливає, що число ступенів вільності Н ланки кінематич­ної пари у відносному русі може змінюватися також від 1 до 5.

Можливі рухи, які ще залишились, можуть бути або незалежними один від одного або зв'язаними один з одним будь-якими додатковими геометричними умовами, наприклад, умовою, що поворот ланки навколо осі на певний кут викликає поступальне переміщення уздовж цієї самої осі на певну відстань (гвинтова пара) і т. ін.

Решта незалежних можливих рухів характеризують число ступе­нів вільності ланок кінематичної пари в їх відносному русі.

Класифікація кінематичних парздійснюється за такими ознаками:

а) числом умов зв'язку, які накладаються кінематичною парою на відносний рух ланок;

б) формою елементів ланок, що утворюють кінематичну пару;

в) способом замикання ланок.

Залежно від числа умов зв'язку(класифікація І. І. Артоболевського), що накладаються кінематичною парою на відносний рух ланок, пари діляться на п'ять класів: І, II,III, IV, V.

Клас кінематичної пари визначається залежністю

S = 6-Н, 2.2)

яка витікає із залежності (2.1).

У багатьох підручниках [18, 19] дається класифікація кіне­матичних пар, запропонована В.В. Добровольським, згідно з якою кінема­тичні пари діляться за числом ступенів вільності Н на одно-, дво-, три-, чотири- і п'ятирухомі.

У табл. 2.1 наведено приклади кінематичних пар та їхні умовні позначення згідно з ГОСТ 2.770-68.

В обертовій парі (див. рис. 2.1, 2.4) ланка А може повертатися на­вколо осі ланки В (або, навпаки, В відносно А), а в поступальній парі рис. 2.5) - переміщатися вздовж пазу ланки В. Число ступенів вільності ланки А в її русі відносно ланки В становить Н = 1, тому число умов зв'язку S = 5, отже ці кінематичні пари V класу.

У гвинтовій парі (рис. 2.6), наприклад, при нерухомій гайці А, гвинт В може повертатися навколо осі х і одночасно переміщатися вздовж цієї самої осі. Проте ці рухи, як вже зазначено, взаємозв'язані, а тому гви­нтова пара є також парою V класу.

Таблиця 2.1