Приклад кінематичних пар

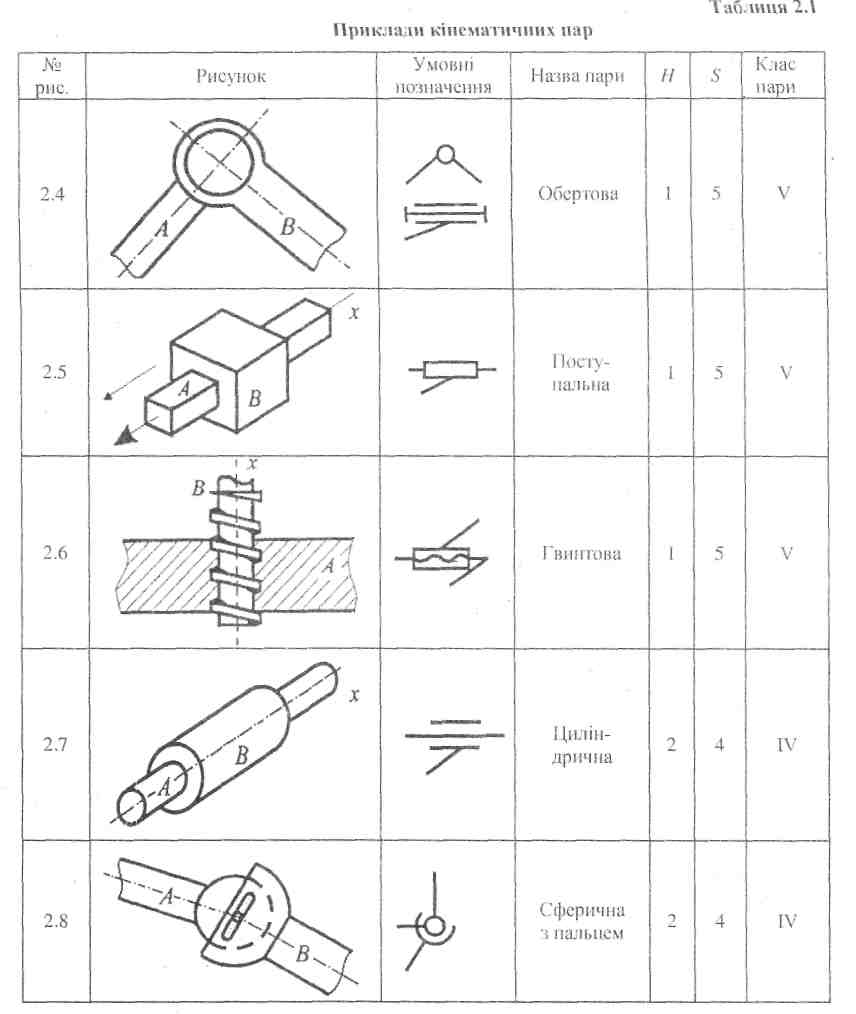
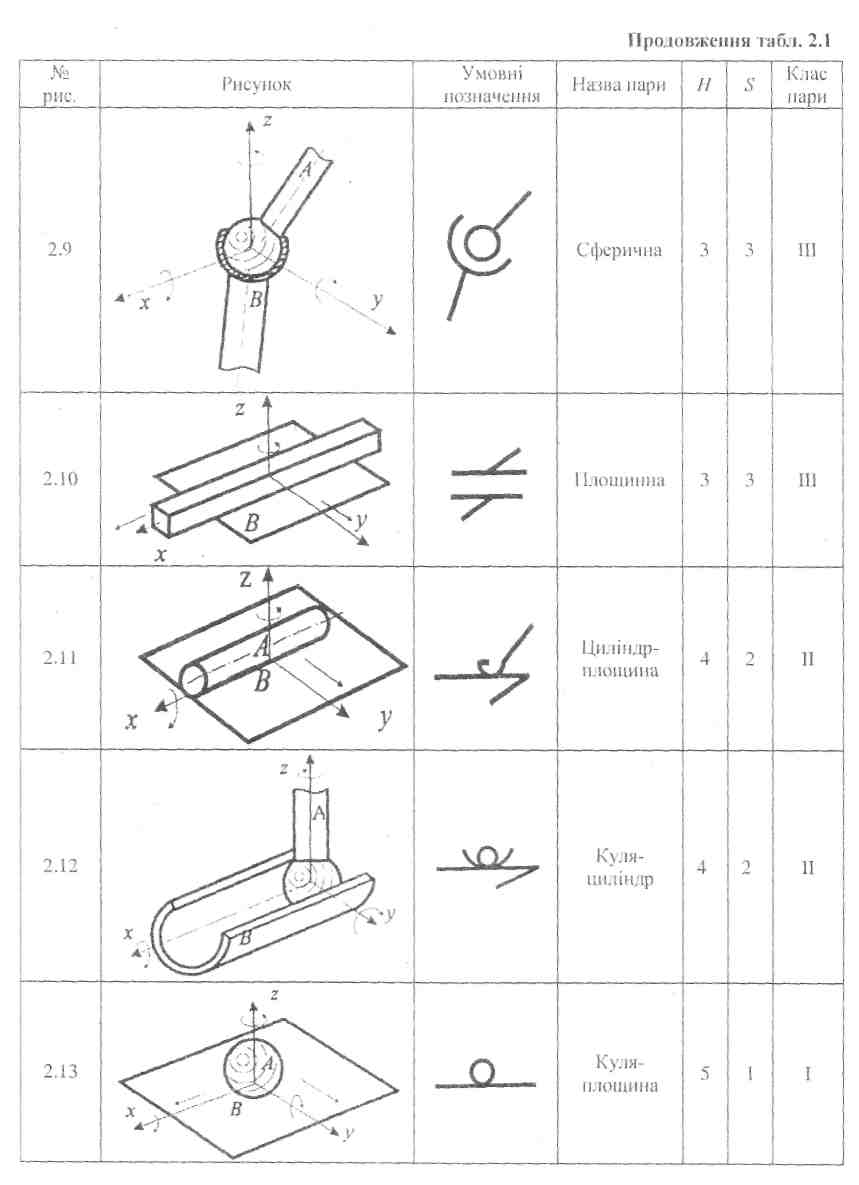
У циліндричній парі (рис. 2.7) втулка В може обертатися навколо осі х циліндра А і переміщатися вздовж неї. Ці рухи незалежні, а тому цю пару необхідно віднести до пари IV класу (H = 2, S = 4) . Це відноситься і до сферичної пари з пальцем (рис. 2.8). Кінець ланки А має форму сфери з пальцем, вісь якого проходить через центр сфери. Ланка В має також сферичну поверхню і паз для пальця. У відносному русі ланка В може по­вертатися навколо осі пальця, а також відносно осі, яка перпендикулярна площині симетрії паза і проходить через центр сфери.

Якщо у парі (рис. 2.8) забрати палець, то одержимо чисто сферичну кінематичну пару (рис. 2.9). Тепер ланка А відносно ланки В (або навпаки) може повертатися навколо однієї з трьох взаємно перпендикулярних осей, які проходять через центр сфери. Тому сферичну пару відносять до IIIкласу (H = 3, S = 3). У площинній кінематичній парі (рис. 2.10) ланка A відносно ланки В (або навпаки) може рухатися вздовж осей х і у, та повертатися навколо осі z. Ця пара також IIIкласу (H = 3, S =3).

Кінематична пара циліндр-площина (рис. 2.11) допускає обертові й поступальні рухи тіла А відносно В відповідно навколо осей х, z і вздовж осей х, у. Тому цю пару відносять до IIкласу (H = 4, S = 2). Так само парою IIкласу є пара куля-циліндр (рис. 2.12), яка допускає, крім трьох обертових рухів, поступальних рух уздовж осі циліндра.

Прикладом пари І класу є пара, схема якої зображена на рис. 2.13. Тут куля А відносно площини В має можливість обертатися навколо трьох осей (х, у, z) та рухатися поступально вздовж осей х і у (H = 5, S=1). Рух кулі вздовж осі z неможливий, бо в один бік він обмежений площи­ною В, а при русі у зворотний бік порушується контакт ланок, і отже, кі­нематична пара перестає існувати.

Залежно від форми елементівкінематичні пари поділяються на нижчі і вищі. Нижчими кінематичними парами називають такі пари, у яких елементи кінематичних пар стикаються поверхнями(див. рис. 2.4 - 2.10). Вищими кінематичними парами називають такі пари, в яких елементи кіне­матичних пар стикаються по лініїабо в точці(див. рис. 2.11-2.13). Слід за­значити, що лінії і точки можуть бути елементами нижчих кінематичних пар. Наприклад, у деяких пристроях елементи обертової пари стикаються окреми­ми лініями і, незважаючи на це, їх не можна назвати вищими, тому що такий самий відносний рух ланок (обертовий) можна одержати стиканням ланок поверхнями.

Нижчі кінематичні пари характеризуються тим, що можуть пере­дати більше зусилля, чим вищі, завдяки більшій площі контакту між лан­ками. Проте витрати на тертя у таких парах більші порівняно з вищими (наприклад, у підшипниках кочення).

Нижчі пари мають властивість інверсії (оборотності руху), тобто характер відносного руху ланок не змінюється від того, яка ланка рухаєть­ся (А відносно B, чи В відносно А, див. рис. 2.4—2.10). Вищі пари такої властивості не мають. Так, при перекочуванні без ковзання циліндра по нерухомій площині (рис. 2.14, а) траєкторія точки М, яка лежить на поверхні циліндра А, буде циклоїда, і навпаки, при обкочуванні без ков­зання площини В навколо нерухомого циліндра А (рис. 2.14, б) точка М площини В буде описувати евольвенту.

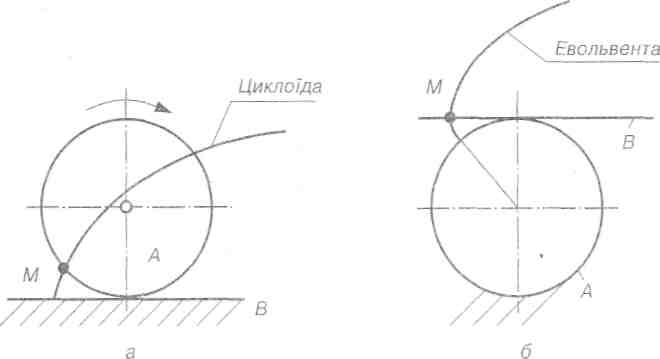
Рис. 2.14. Траєкторія точки М при перекочуванні:

а) циліндра (кола) відносно площини (прямої); б) площини відносно циліндра

У сучасних механізмах найбільш поширені кінематичні пари V і IV класів.

Для того, щоб елементи кінематичних пар перебували у постійному контакті, пари повинні бути замкнутими. Замикання може бути геометрич­ним або силовим.Геометричне замикання здійснюється відповідною геоме­тричною формою елементів ланок кінематичної пари або конструкцією кіне­матичної пари. Наприклад, усі пари, які зображено на рис. 2.4-2.9, 2.12, замкнуті геометрично, тому що стикання елементів цих пар забезпечується їхніми геометричними формами. Для того щоб пари, зображені на рис. 2.10, 2.11, 2.13, були замкнуті, необхідно тіло А притискати до площини В будь-якою силою. Силове замикання забезпечується силою ваги, силою пружності пружини тощо.