Аэродинамические трубы и испытания в них. Получение аэродинамических коэффициентов. Закон аэродинамического подобия

В предыдущих параграфах мы убедились в том, что, зная коэффициент аэродинамической силы, можно, исходя из формулы основного закона, вычислить величину силы. Этим путем и идет инженер-конструктор при так называемом аэродинамическом расчете самолета. Пользуясь коэффициентами, полученными при аэродинамических испытаниях, он может вычислить подъемную силу и лобовое сопротивление проектируемого им самолета, а тем самым определить летные свойства будущего самолета.

Таким образом, на практике аэродинамические силы находят но их коэффициентам. При аэродинамических же испытаниях (в аэродинамических лабораториях) решается как раз обратная задача: при помощи особых весов измеряют аэродинамические силы, возникающие у модели под действием воздушного потока, а затем, исходя из той же формулы основного закона, находят численные значения коэффициентов. Об этом мы и расскажем вкратце ниже, а попутно дадим дополнительные сведения об аэродинамических трубах и тех принципах, которые кладутся в основу аэродинамических испытаний.

Аэродинамическая труба состоит из следующих основных частей (рис. 113): 1) всасывающей воронки или коллектора С; 2) спрямляющей решетки Н; 3) цилиндрической рабочей части D, в которой и помещается испытуемое тело (например модель крыла); 4) диффузора Е; 5) вентилятора В; 6) электромотора А.

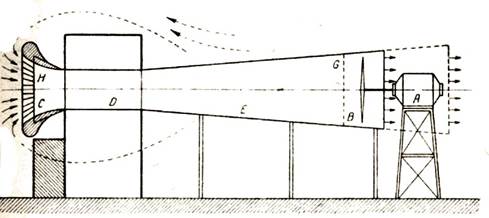
Рис. 113. Аэродинамическая труба незамкнутого типа

При пуске в ход вентиляторно-моторной установки воздух через коллектор всасывается в трубу и через спрямляющую решетку попадает в рабочую часть. Назначение спрямляющей решетки — выпрямлять косо идущий поток; в результате — в рабочей части поток движется уже параллельно стенкам трубы. В рабочей части (наиболее узкой) скорость потока максимальная, в диффузоре же вследствие расширения потока скорость постепенно падает. В конце диффузора перед вентилятором установлена металлическая предохранительная сетка G. Из диффузора воздух выбрасывается в помещение.

Такая труба называется трубой незамкнутого типа. Достоинства этого типа трубы: простота конструкции и удобство наблюдения при опытах. Недостатки: значительные размеры помещения, необходимого для установки трубы, и неэкономичность.

Другим типом трубы является труба замкнутого типа (рис. 114). В такой трубе оба конца, ее, выходной и входной, замыкаются на себя (цилиндрическая часть трубы — рабочая часть). Нетрудно понять, что в такой трубе циркулирует все время один и тот же объем воздуха. Благодаря этому значительно уменьшается затрата энергии на перемещение воздуха в трубе. Основные части такой трубы в общем те же, что и у трубы незамкнутого типа.

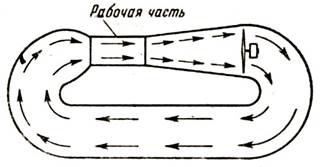
Рис. 114. Схема аэродинамической трубы замкнутого типа

Аэродинамическая труба является, как уже упоминалось, основным прибором аэродинамических лабораторий. Вторым весьма важным прибором являются аэродинамические весы, служащие для измерения аэродинамических сил, возникающих у модели под действием воздушного потока.

Конструкции аэродинамических весов (существуют различные типы) довольно сложны, и описывать их мы не будем. Заметим лишь, что устройство аэродинамических весов основано на том простом принципе, известном нам из механики, что всякую силу можно измерить, при помощи силы веса, принятой за единицу силы (1 кг). Измерение аэродинамических сил будет показано ниже на схеме простейших аэродинамических весов.

Размеры современных самолетов и даже их частей (крыльев, фюзеляжа) бывают настолько велики, что часто совершенно исключают возможность испытания их в натуре. Поэтому аэродинамические испытания производят на моделях. Моделью называется тело точно такой же формы, как и натура, но сделанное в значительно меньшем масштабе (обычно от 1/5 до 1/20).

Модели делают чаще всего из дерева (модели самолетов, модели крыльев, модели фюзеляжей и т. д.). Все линейные размеры модели должны быть в одинаковое число раз меньше соответствующих размеров натуры. В таком случае модель будет геометрически подобна натуре.

Геометрическое подобие — необходимое условие при аэродинамических испытаниях. Однако одного этого условия недостаточно. Должно быть соблюдено еще одно весьма важное условие. Прежде чем говорить об этом условии, посмотрим, как производятся испытания в трубе для получения численных значений аэродинамических коэффициентов.

Рассмотрим сначала наиболее простой случай — получение коэффициента си ы сопротивления при симметричном обтекании, т. е. коэффициента лобового сопротивления С_x.

Пусть, например, надо найти коэффициент лобового сопротивления фюзеляжа заданной формы. Модель такого фюзеляжа устанавливают в рабочей части трубы на аэродинамических весах, простейший вид которых схематически показан на рис. 115.

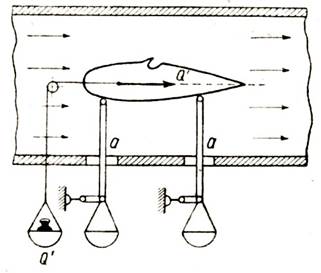
Рис. 115. Схема простейших аэродинамических весов для измерения лобового сопротивления модели

Рычажки аа весов могут свободно перемещаться вдоль трубы Модель устанавливают так, чтобы продольная ось ее была параллельна потоку, иначе говоря — модель фюзеляжа ориентируют относительно направления потока совершенно так же, как ориентирован относительно встречного потока фюзеляж самолета в полете.

Затем пускают в ход вентилятор. Так как рычажки весов аа, на которых укреплена модель, могут свободно перемещаться горизонтально вдоль трубы, то, очевидно, под действием силы лобового сопротивления Q' модель станет перемещаться назад, т. е. по потоку, если силу Q' не уравновесить равной ей силой, направленной в противоположную сторону (аэродинамические силы, возникающие у модели, будем обозначать со значком „прим“).

Этой силой служит вес гири, положенной на чашку, к которой прикреплена нить, перекинутая через блок и привязанная к переднему концу модели. Если уравновесить модель так, чтобы она осталась неподвижной, то, очевидно, вес гири Q' и даст нам величину силы лобового сопротивления модели.

Обозначая плотность воздуха при испытании через р', площадь миделя модели через S' и скорость потока в трубе через V', найдем лобовое сопротивление модели: Q = C_xp’S’V’².

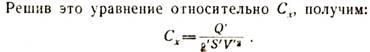
Все величины, входящие в правую часть этой формулы, определимы из опыта: величину силы Q' определяют вышеописанным методом; плотность воздуха р' нетрудно вычислить, имея показания барометра и термометра, находящихся в помещении, в котором производятся испытания; площадь миделя S’ модели, конечно, известна; скорость потока V’ в трубе измеряют во время опыта трубкой Пито (в соединении с микроманометром). Таким образом, численное значение коэффициента лобового сопротивления испытуемого тела (в нашем случае — фюзеляжа заданной формы) найти, как видим, не трудно.

Методом, аналогичным описанному, находятся и коэффициенты аэродинамических сил, возникающих при несимметричном обтекании.

Пусть, например, надо найти численные значения коэффициентов подъемной силы и лобового сопротивления (Су и С_х) для крыла заданной формы при некотором угле атаки а (например при а = 3°). Модель крыла устанавливают в рабочей части трубы на аэродинамических весах под заданным углом атаки α (рис. 116).

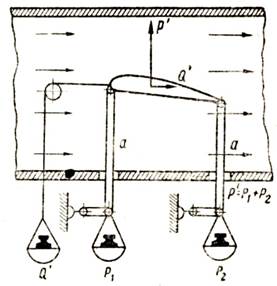
Рис. 116. Схема простейших аэродинамических весов для измерения подъемной силы и лобового сопротивления модели крыла

Установка модели крыла под заданным углом атаки производится при помощи угломерного прибора. Модель устанавливается так, чтобы относительно направления потока она была ориентирована совершенно так же, как ориентировано крыло летящего самолета относительно встречного потока. Затем пускают вентилятор.

Под действием потока модель разовьет подъемную силу Р' и будет испытывать лобовое сопротивление Q'. Заметим, что рычажки аа весов могут свободно перемещаться не только горизонтально (вдоль трубы), но и вертикально. Таким образом, если силы P’ и Q’ не уравновесить, то под действием их модель переместится вверх и назад (по направлению полной силы сопротивления).

Силу Q' можно уравновесить гирей Q', вес которой и даст величину силы лобового сопротивления модели. Подъемную же силу Р' можно уравновесить двумя гирями P₁ и P₂. Очевидно, сумма их и будет равна подъемной силе P’.

Зная величины сил Р’ и Q', нетрудно определить и их коэффициенты. Из формулы подъемной силы

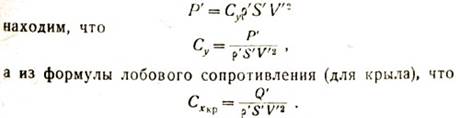
Подставив в правые части этих формул найденные при испытании модели крыла величины сил Р’ и Q' и числовые значения остальных величин, находят (произведя необходимые вычисления) числовые значения коэффициентов С_у и С_х для крыла данной формы при угле атаки α.

Производя испытание данной модели при другом угле атаки а (например при α = 5°), получают другие величины сил Р' и Q' (ибо, как мы знаем, силы Р и Q изменяются при изменении угла атаки). Подставляя эти новые значения сил Р' и Q' в формулы для коэффициентов (и производя необходимые вычисления), получают новые значения С_у и С_х, соответствующие новому углу атаки. Испытывая модель при различных углах атаки (обычно —от первого летного до критического), получают таким образом ряд значений С_у и С_х в зависимости от угла атаки.

Описанный способ испытаний в аэродинамической трубе называется продувкой.

Итак, мы познакомились с методом получения аэродинамических коэффициентов. Задача по отысканию коэффициентов сводите , как видим, к измерению аэродинамических сил, возникающих у модели. Конструктор же, повторяем, решает обратную задачу. Он намечает (согласно заданию) размеры и полетные данные проектируемого им самолета и, пользуясь аэродинамическими коэффициентами, по известным уже нам формулам вычисляет действующие на самолет силы.

В результате таких подсчетов конструктор На основании лишь лабораторных опытов с маленькими моделями получает возможность сделать, как уже было упомянуто, аэродинамический расчет самолета, т. е. определить скорость самолета, его потолок, грузоподъемность и т. д. Способ, как видим, очень удобный и как будто бы несложный.

Оказывается, однако, что переход от модели к натуре при помощи аэродинамических коэффициентов далеко не прост. Для того чтобы коэффициенты, полученные при испытании модели, были применимы к натуре, необходимо, оказывается, соблюдение не только геометрического подобия, но и аэродинамического подобия.