Полная сила сопротивления, подъемная сила и лобовое сопротивление крыла и их коэффициенты. Качество крыла

Из механики нам известно, что сила будет вполне определена, если найдены ее величина, направление и точка приложения. Это относится, конечно, и к силам сопротивления воздуха.

Из предыдущего мы уже знаем, что величину силы лобового сопротивления при симметричном обтекании находят по основному закону; что же касается ее направления и точки приложения, то они известны, так как сила лобового сопротивления всегда направлена по потоку (см. рис. 82) и точка ее приложения лежит на оси симметрии тела (в какой именно точке оси — значения не имеет, поскольку точку приложения силы можно переносить в любое место по линии действия силы).

Сопротивление воздуха при несимметричном обтекании тоже, конечно, подчиняется основному закону. Иными словами, величина полной силы сопротивления R крыла (рис. 101) прямо пропорциональна плотности воздуха, площади крыла, квадрату скорости и зависит от формы крыла, но, кроме того, зависит еще от величины угла атаки. С изменением величины у ла атаки величина силы сопротивления будет изменяться. Это означает, что с изменением угла атаки будет изменяться и величина коэффициента сопротивления.

Следовательно, при несимметричном обтекании у тела (крыла, пластины) нет постоянного коэффициента сопротивления С (как это имеет место при симметричном обтекании), а каждому углу атаки α (рис. 102) соответствует свой коэффициент, который и принято поэтому обозначать С_α. Коэффициент С_α называется коэффициентом полной силы сопротивления. Заменяя в формуле основного закона коэффициент С на C_α, мы получим следующую формулу для определения величины полной силы сопротивления R_α (индекс α ставят иногда, чтобы показать, что вычисляется то сопротивление, которое испытывает крыло или пластина при угле атаки α): Rα = C_αpSV².

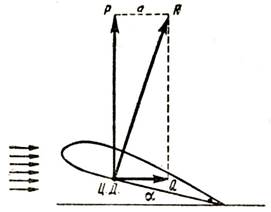
Рис. 102. Схема сил, действующих на крыло

Величина подъемной силы Р и величина лобового сопротивления Q крыла находятся аналогичным же способом. Силы Р и Q являются составляющими силы R и, следовательно, также подчиняются основному закону. Очевидно, величина каждой из них, как и силы R, зависит не только от формы крыла, но и от величины угла атаки α.

Зависимость подъемной силы Р от формы крыла и от угла атаки дает коэффициент подъемной силы, обозначаемый С_у. Зависимость лобового сопротивления Q от формы крыла и от угла атаки дает коэффициент лобового сопротивления (обозначается, как и при симметричном обтекании, через С_х). Учитывая сказанное, получаем следующие формулы для определения величин сил Р и Q:

Коэффициенты С_α, C_у и С_х находятся опытным путем, т. е. при испытании моделей крыльев в аэродинамической трубе (об этом будет рассказано в следующих публикациях, и тогда станут понятны обозначения коэффициентов подъемной силы и лобового сопротивления).

Обращаем внимание учащегося на то, что формула лобового сопротивления крыла имеет такой же вид, как и формула лобового сопротивления при симметричном обтекании. Но не следует забывать, что коэффициент С_х в случае симметричного обтекания зависит только от формы тела, т. е. постоянен; коэффициент же С_х крыла зависит не только от формы крыла, но и от угла атаки, т. е. непостоянен (при различных углах атаки имеет различные численные значения). Для того чтобы показать, что вычисляется лобовое сопротивление крыла, последнюю формулу иногда пишут так:

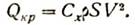
Если же вычисляют коэффициент, то пишут: С_Хкр. Рассматривая рис. 102, нетрудно обнаружить, что между силами R, Р и Q имеется определенное геометрическое соотношение. Мы видим, что сила Q равна отрезку а, который является катетом прямоугольного треугольника, другим же катетом является сила РУ а сила R — гипотенузой; так как квадрат гипотенузы равен сумме квадратов катетов, то очевидно:

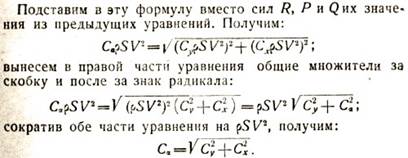
Мы видим, что соотношения между коэффициентами С_α, С_у и С_х совершенно такие же, как и между силами R, Р и Q. Это означает, что аэродинамические коэффициенты можно рассматривать как некоторые силы и, следовательно, можно оперировать с ними, как с векторами (рис. 103).

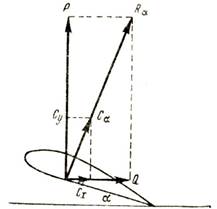
Рис. 103. Аэродинамические силы и их коэффициенты

Последняя схема наглядно показывает, что аэродинамические силы пропорциональны их коэффициентам; например P/Q = C_y/C_x (это нетрудно доказать и алгебраически, стоит лишь разделить уравнение подъемной силы на уравнение лобового сопротивления).

Итак, мы узнали, как находят величину полной силы сопротивления, подъемной силы и силы лобового сопротивления крыла и какие существуют соотношения между этими силами и их коэффициентами.

Поговорим теперь о направлении сил Р, Q и R. Направление подъемной силы Р и направление силы лобового сопротивления Q неизменны : подъемная сила всегда направлена перпендикулярно потоку, т. е. линии полета, а сила лобового сопротивления всегда направлена по потоку, т. е. обратна направлению полета (рис. 104).

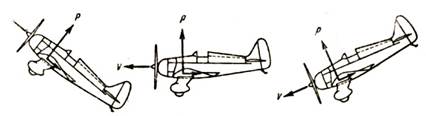
Рис. 104. Подъемная сила всегда перпендикулярна направлению полета, а сила лобового сопротивления всегда обратна направлению полета

Направление полной силы сопротивления R не перпендикулярно хорде крыла (рис. 105) и зависит от угла атаки (а у разных крыльев и от формы крыла). Следовательно, направление силы R надо уметь определить. Направление силы определяют по величине угла, который сила составляет с какой-нибудь условной линией, направление которой известно. В данном случае такой линией считают перпендикуляр к направлению потока. Таким образом, для определения направления силы R приходится определять угол между направлениями сил R и P.

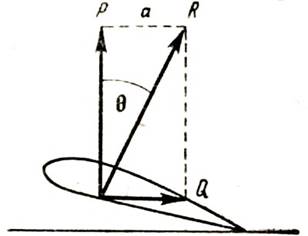
Рис. 105. Определение направления полной аэродинамической силы

Этот угол обозначают θ (греч. буква „тэта“). Из прямоугольного треугольника, образованного этими силами и отрезком α равным силе Q, можно определить тангенс угла θ. Тангенсом угла называется отношение катета, противолежащего углу, к катету прилежащему; поэтому

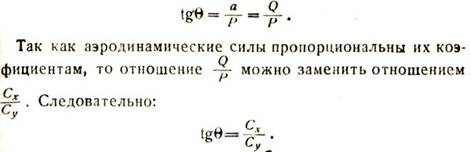
Коэффициенты С_х и С_у определимы опытным путем для любого крыла и при любых углах атаки и, значит, определить тангенс угла θ нетрудно. Зная тангенс, легко найти и величину угла θ (по тригонометрическим таблицам). Заметим, что угол θ иногда называют углом качества. Чем объясняется такое название, мы увидим дальше.

Выше было упомянуто, что величина и направление полной силы сопротивления R изменяются в зависимости от формы крыла и в особенности от величины угла атаки (так как от этих факторов зависит характер обтекания крыла). Глядя на рис. 105, нетрудно сообразить, что с изменением величины и направления силы R будет изменяться величина ее составляющих: подъемной силы Р и лобового сопротивления Q (направления их остаются неизменными). Однако изменяются силы Р и Q неодинаково.

У большинства крыльев подъемная сила бывает равна нулю (рис. 106, I) при небольшом отрицательном угле атаки (примерно от — 2 до — 8°, в зависимости от формы профиля). Угол атаки, при котором подъедая сила равна нулю, называют первым лётным углом (на этом угле и на близких к нему самолет пикирует).

При нулевом значении угла (рис. 106, II) подъемная сила уже значительна и при дальнейшем увеличении угла атаки непрерывно увеличивается (рис. 106, III), достигая максимальной величины при α = 14—18° (рис. 106, IV), а затем резко уменьшается (рис. 106, V).

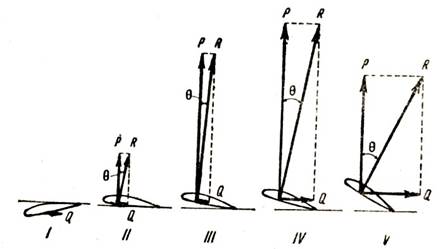
Рис. 106. Изменение сил сопротивления крыла при изменении угла атаки

Угол атаки, при котором подъемная сила достигает максимальной величины, называется критическим или посадочным углом атаки (примерно на этом угле осуществляется посадка самолета). На углах атаки выше критического самолет летает редко, поэтому о них говорить не будем. Таким образом, лётными углами атаки являются углы от первого лётного до критического (лётный диапазон углов).

Из приведенных схем видно, что лобовое сопротивление крыла изменяется иначе. Лобовое сопротивление никогда не бывает равно нулю. При малых отрицательных, нулевом и малых положительных углах атаки лобовое сопротивление относительно невелико и меняется мало. На средних углах атаки (примерно 3—6°) лобовое сопротивление начинает заметно увеличиваться и при дальнейшем увеличении угла атаки быстро растет.

Изменение подъемной силы и лобового сопротивления крыла в зависимости от угла атаки чрезвычайно важный вопрос, и позже мы рассмотрим его более подробно.

Все сказанное об изменении подъемной силы и лобового сопротивления крыла в зависимости от угла атаки полностью относится и к коэффициентам этих сил С_у и С_х, поскольку последние пропорциональны силам Р и Q (т. е. мы можем сказать, что при некотором отрицательном угле атаки C_у равен нулю, что при критическом угле атаки С_у достигает максимальной величины, что С_х никогда не равен нулю и т. д.). Это следует твердо запомнить, так как в дальнейшем нам часто придется оперировать не аэродинамическими силами, а их коэффициентами.

Характер изменения подъемной силы и лобового сопротивления в зависимости от угла атаки позволяет сделать следующий очень важный вывод.

Подъемная сила дает возможность осуществлять полет, лобовое же сопротивление лишь тормозит движение; поэтому мы заинтересованы, конечно, в том, чтобы подъемная сила крыла была как можно больше. Однако если подъемная сила будет очень велика и лобовое сопротивление будет весьма большим, то крыло будет работать невыгодно, так как большое лобовое сопротивление будет уменьшать скорость полета.

Мы видели, что на критическом угле атаки (и на углах, близких к нему) подъемная сила очень велика. но и лобовое сопротивление настолько значительно, что подъемная сила превосходит лобовое сопротивление всего лишь в 4-6 раз (примерно). На средних же углах атаки подъемная сила, хотя и несколько меньше, зато лобовое сопротивление много меньше, и подъемная сила превосходит лобовое сопротивление в 15—20 раз.

Отсюда ясно, что оценивать работу крыла на том или ином угле атаки следует не по абсолютной величине подъемной силы, а по отношению величины подъемной силы к величине лобового сопротивления, т. е. по отношению P/Q. Это отношение и называется поэтому аэродинамическим качеством, или просто качеством крыла (обозначается буквой к). Таким образом, качество крыла к = P/Q, а переходя на коэффициенты, будем иметь: k = C_y/C_x

Итак, качество крыла показывает, во сколько раз подъемная сила больше лобового сопротивления, или иначе, во сколько раз коэффициент подъемной силы больше коэффициента лобового сопротивления.

Испытания крыльев в аэродинамической трубе показывают, что на очень малых углах атаки (близких к 0 ) крылья в большинстве случаев имеют небольшое качество (иногда говорят: плохое качество). При увеличении угла атаки качество увеличивается (улучшается) и при некотором вполне определенном для каждого крыла угле атаки достигает наибольшей величины. Угол атаки, при котором качество достигает наибольшей величины, называется наивыгоднейшим углом атаки.

При дальнейшем увеличении угла атаки, несмотря на возрастание С_у, но вследствие еще более быстрого возрастания С_х, качество уменьшается, и резко уменьшается, начиная с критического угла атаки. Указанные изменения качества в зависимости от угла атаки понятны из приведенных схем (рис. 106) и замечаний к ним.

У большинства современных крыльев наибольшее (максимальное) качество достигает 20 (при наивыгоднейшем угле атаки), у очень хороших — даже 22. У плоской пластины качество не превышает 8 (отсюда ясно, почему крылья невыгодно делать плоскими).

В аэродинамике иногда применяется так называемое обратное качество. Обратным качеством называется отношение С_х/С_у. Следовательно, обратное качество показывает, какую часть от C_у составляет С_х (у большинства современных крыльев обратное качество достигает 1/20, у очень хороших — даже 1/22.

Из рис. 106 нетрудно видеть, что качество будет тем больше, чем меньше угол θ. Поэтому угол θ и называют иногда углом качества.

Мы выяснили, как находят величину и направление полной силы сопротивления и величину каждой из ее составляющих : подъемной силы и силы лобового сопротивления. Но все эти три силы могут быть вполне определены только в том случае, если будет известна и точка их приложения, т. е. центр давления крыла. Из предыдущего параграфа мы знаем, что центром давления называют точку пересечения полной аэродинамической силы с хордой крыла.

Однако положение центра давления на хорде непостоянно и меняется в зависимости от угла атаки. Как меняется положение центра давления и как находят положение центра давления на хорде — вопросы сложные, и мы расскажем о них позже в отдельном параграфе. Пока же заметим, что на малых углах атаки у большинства крыльев центр давления находится приблизительно на 1/3 длины хорды от передней кромки крыла.